machine learning - andrew ng | 临时个人主页

图片比较多，加载方法也比较笨，好在可以记忆浏览位置，如果有载图错误直接刷新即可。

代码笔记见此处。

第一章引言

1-1 欢迎

机器学习应用：

Database mining
- large datasets from growth of automation/web.
- e.g., Web click data, medical records, biology, engineering
Applications cannot program by hand.
- e.g., Autonomous helicopter, handwriting recognition, NLP, CV
Self-customizing programs
- e.g., Amazon product recommendations
Understanding human learning (brain, real AI)

1-2 What is ML

经验E、任务T、度量P：机器学习是 T, measured by P, improves with E.

ML algorithms:

Supervised learning（监督学习）
Unsupervised learning（无监督学习）
Others: Reinforcement learning（强化学习）, recommender systems（推荐系统）

1-3 监督学习

“right answers” given：给一个数据集，含有一部分正确答案。使用监督学习算法得到对应关系。

监督学习类型：

regression（回归问题）：输出具体值。如估计房价
classification（分类问题）：输出离散值。如判断肿瘤

Q：实际问题，有多个attributes和多个features，甚至无穷个，如何处理？

A：以支持向量机算法为例，有数学方法来处理无穷多的features。

1-4 无监督学习

给定数据集没有label，不知道有哪些类型。使用无监督学习算法寻找数据中的结构。

无监督学习类型：

使用clustering（聚类算法）来自动分簇。

如：新闻分簇，DNA分组；组织计算机群、社交网络分析、市场分割、天文数据分析。
Cocktail party problem，两个麦克录下两个人同时说话，将他们分离。

第二章单变量线性回归（Linear Regression with One Variable）

2-1 regression模型描述

训练集

m =训练样本的个数
x = input variable/features
y = output variable/features
(x, y) = 一个训练样本
(x⁽ⁱ⁾, y⁽ⁱ⁾) = 第i个样本

机器学习算法从训练集得出函数h（hypothesis），表示从x到y的对应关系。

在预测房价问题上，假定h是一元一次函数。

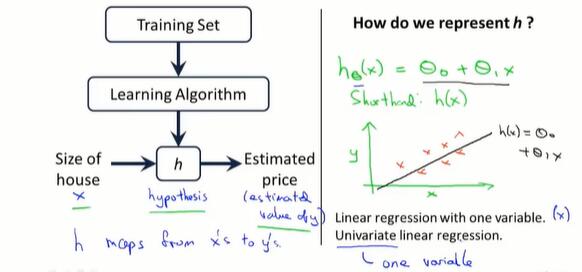
2-2 代价函数（cost function）

现在有h函数：$h_\theta(x) = \theta_0 + \theta_1x$，还有一个训练集。

我们的目的是寻找h函数中的两个参数θ₀、θ₁，让h_θ(x)拟合实际y.

定义代价函数，计算h和y的差，要让其取最小，表达式如下：

$$minimize_{\theta_0, \theta_1} \frac{1}{2m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)}})^2$$

也就是使代价函数 $ J({\theta_0, \theta_1}) = \frac{1}{2m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)}})^2 $ 取到最小值。

2-3 代价函数的直观理解I

Hypothesis: $h_\theta(x) = \theta_0 + \theta_1x$
Parameters: $\theta_0, \theta_1$
Cost Funcion: $J({\theta_0, \theta_1}) = \frac{1}{2m}\sum_{i=1}^{m}({h_\theta(x^{(i)})-y^{(i)}})^2$
Goal: $minimize_{\theta_0, \theta_1} J({\theta_0, \theta_1})$

取不同的θ₀θ₁，得到不同的h(x)，对应不同的J(θ₀, θ₁).

下图是只有一个变量的简化情况，此时可以画出一元函数 J(θ₁) 的曲线。

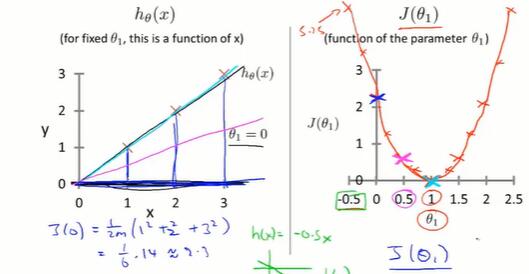
选择θ，使J的值最小化。此时h函数最好地拟合了现实情况。

2-4 代价函数的直观理解II

有两个参数时，得到 J(θ₀, θ₁) 的三维图像。

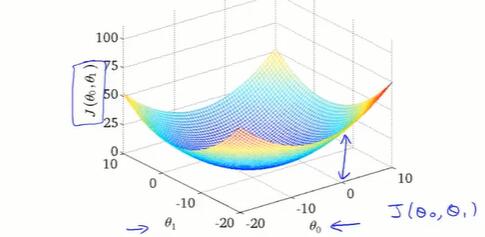
可以用等高线图在平面上展示。中心点处函数值最小。

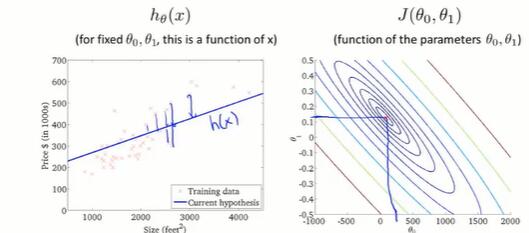
我们希望有一个算法，来自动找到使 J 最小的参数 θ .

2-5 梯度下降（gradient descent）

开始时，给θ设置初始值；
改变θ，使 J 的值减少，直到取到了局部最小值；
重复上个过程。

直观解释：

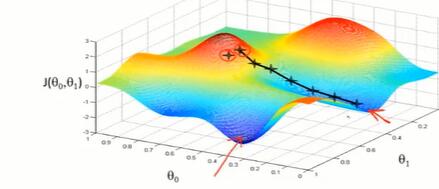
不同的初始点可能走到不同的结束点。

数学解释：

α 是学习率，表示梯度下降的步幅大小。偏导数表示梯度下降的方向。

需要注意的是，要让多个 θ 同时更新。先计算多个temp值，再一起赋新值。

2-6 梯度下降的直观理解

偏导数的直观解释：

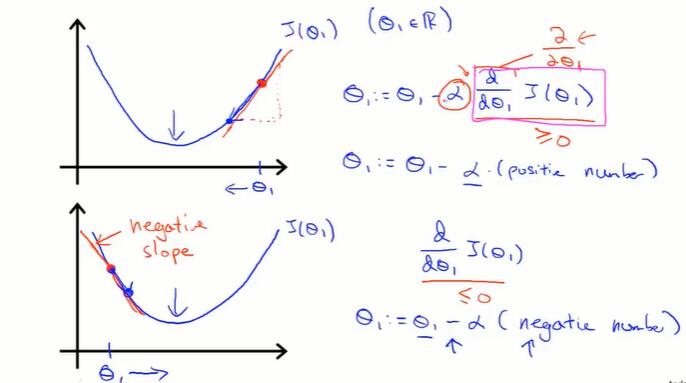
以单个变量的函数为例。偏导数的值保证了 $\theta$ 一定朝 $J(\theta)$ 下降的方向变化。

学习率 α 的直观解释：

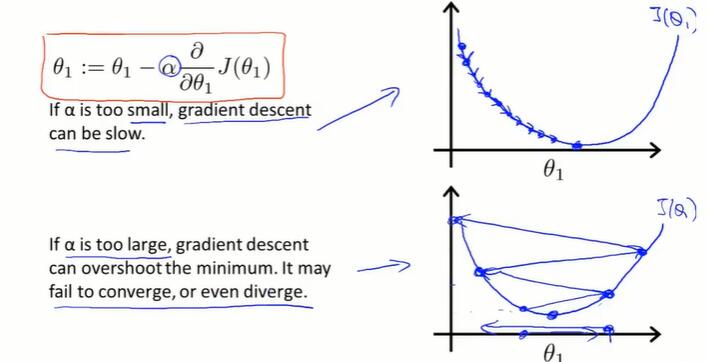
α 太小，步数太多；α 太大，会导致无法收敛甚至发散。

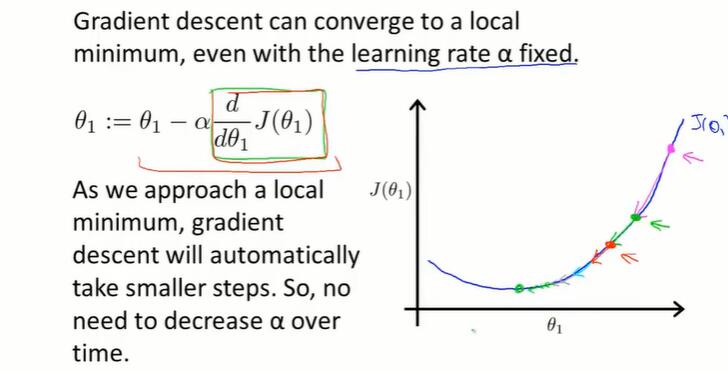
在到达optimum点后，偏导数值为0，梯度下降算法就什么也不做了。

当学习率 α 不变时，梯度下降进行的过程中，偏导数通常会变小，因此每一步下降幅度会减小。

因此在接近局部最小值时，步子会变小。

2-7 线性回归的梯度下降

这个梯度下降算法称为 batch 梯度下降。

原因是：每一步梯度下降，都计算了整个训练集m个样本的插值平方总和。

也有方法不全览整个训练集，每次只关注小子集。这将在之后介绍（17.2-17.4）。

接下来的课：

在线性代数上，存在一个解法，可以在不需要多步梯度下降的情况下，也能解出代价函数的最小值，这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下，梯度下降法比正规方程要更适用一些。
梯度下降的通用算法

第三章线性代数

3-1 矩阵和向量

向量是一个 n × 1 的矩阵。

默认的下标从1开始。

3-2 加法和标量乘法

3-3 矩阵与向量相乘

一元线性回归可以转换成矩阵和向量相乘。

下图是矩阵和向量的构造方法，以及代码。

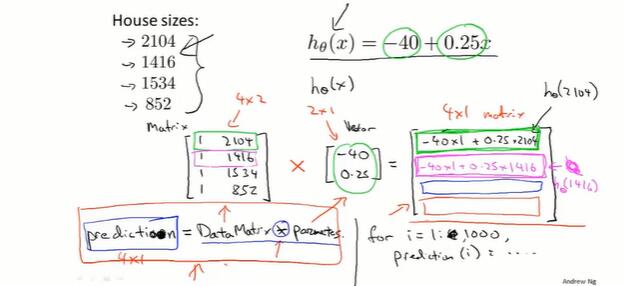
3-4 矩阵乘法

3-5 矩阵乘法的性质

矩阵乘法是：

不可交换的 A × B ≠ B × A
可结合的 (A × B)× C = A ×(B× C）

单位矩阵 I ：

A · I = I · A = A

3-6 逆、转置

矩阵的逆

AA^-1 = A^-1A = I ，A是满秩方阵

矩阵的转置

A^T_ij = A_ji

第四章多变量线性回归（Linear Regression with Multiple Variables）

4-1 多维特征

从只有1个变量的情况，推广到有m组n维特征的情况。

$h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + … + \theta_nx_n$

设x₀ = 1，则$h_\theta(x) = \theta^Tx$（写成向量内积表达式）

4.2 多变量梯度下降

4.3 梯度下降技巧1-特征缩放

当多个特征取值范围相差很大，梯度下降收敛得很慢。

因此，进行Feature Scaling，将每个特征都控制在约 -1 ≤ x_i ≤ 1 的范围内。

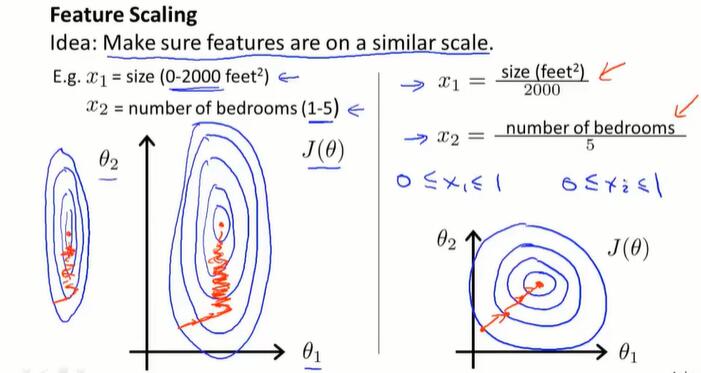
除了除以最大值，还有一个均值归一化的工作（mean normalization），让特征的均值接近0.

具体做法是用（x_i - μ_i）代替 x_i。

4.4 梯度下降技巧2-学习率

绘制随迭代次数增加，代价函数值的变化图象，来确定梯度下降算法在正常运行。

也可以用设置阈值（检测平滑）的方式自动测试，但确定阈值是困难的。看图像在大多数时候更方便直观。

当代价函数曲线是上升的或不收敛，通常的解决方法是使用更小的 α 值。

α 太小会让收敛变得很慢，多试几次，选一个合适的 α 值。

4.5 选择合适的特征和多项式回归（polynomial regression）

通过对函数图像的了解，和对数据的了解，选择合适的特征，来获得更好的模型。

如预测房屋价格，可以选择房屋的size，或者房屋的宽度等特征。

用多项式回归（polynomial regression）来理解选择特征：

作简单的处理来拟合多项式模型：让x_i为size的i次方，或对size开方。

在这种指数变换的情况下，做特征scaling是很有必要的。

也有些算法能够观察给出的数据，自动选择特征。

4.6 正规方程

对于某些线性回归问题，正规方程可以求解参数 θ 的最优值。

正规方程：

当 θ 是一个实数，让代价函数导数为0，可以解出 θ 的值。（函数求极小值，找导数为 0 的点）

推广到 θ 是向量，通过设置代价函数的偏导数为0，求解 θ 。

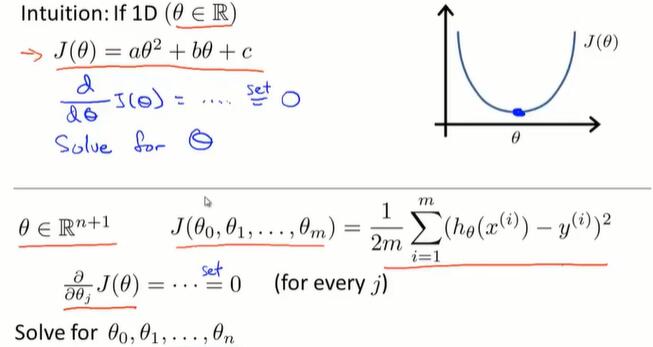
具体做法：构造 m*(n+1) 矩阵 X 和 m 维向量 y ，用最小二乘法计算 θ 。

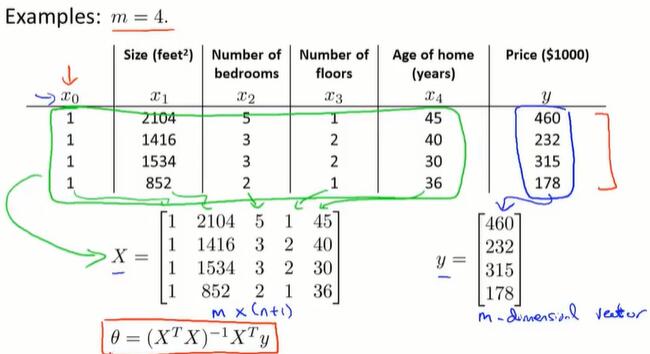
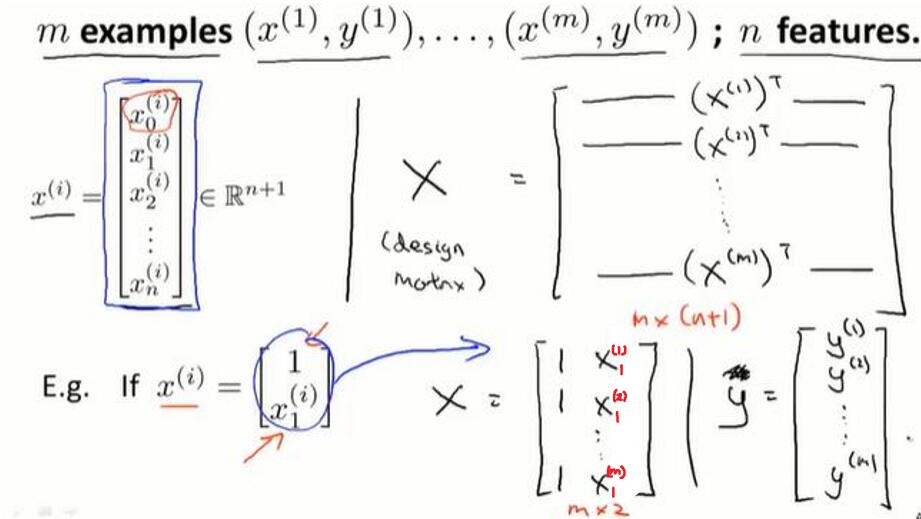
使用正规方程法，不需要做特征scaling。

线性回归问题的求解参数 θ：

梯度下降：在减小代价函数的过程中，迭代变换 θ 。
- 需要选择 α 并进行需要多次迭代
正规方程：解析求解，只需一步。
- n 很大时，(X^TX)^-1 很难算（可以把 n=10000 当作进行选择的边缘）

4.7 *正规方程及不可逆性

使用正规方程求解参数 $\theta = (X^TX)^{-1}X^Ty$ 时，如果：

X^TX不可逆时（其实发生得很少）

咋办？如在Octave里，有求伪逆的函数 pinv，矩阵不可逆时也可以正常求解。
原因？矩阵不满秩。
- 多个 x 线性相关。修改冗余的特征
- m≤n（特征多，数据少）。用正则化（regularization）解决

第五章 Octave Tutorial

由于Octave不再具有先进性，我学习了Python3的numpy和pandas库，笔记见代码和注释。

（todo：此处总结成一篇文章后，链接到博客）

5.6 向量化

将一般的运算转化成使用线性代数库的矩阵、向量运算。

在线性回归问题，同步更新θ的问题上，向量运算如下：

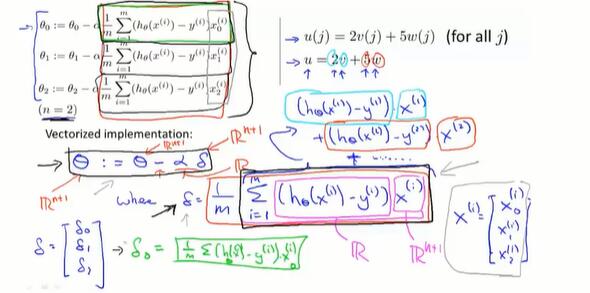
θ 是向量，α 是数，δ 是向量。最终目的是更新 θ 向量。
对于 δ ，是由多个数组成的向量。
- δ_k 由 h-y和x_k⁽ⁱ⁾相乘再相加而来，h-y是差值是一个数，x_k⁽ⁱ⁾是第i行第k个属性值也是一个数，δ_k 就是一个数。
- δ 是由数组成的向量。
- 整体上，也可以看做图片上 $u = 2v + 5w$ 的向量相加形式：先纵向形成向量，所有的h-y是一样的，也就是是一个倍数，x是第i行数据的一个向量。δ就像u一样，做类似的向量×系数再相加。

第六章逻辑回归（Logistic Regression）

当要预测的 y 是离散的，就是 Classification 问题。

Logistic Regression 算法就是一个广泛应用的 Classification 算法。

6.1 分类问题（classification）

Q：为什么线性回归不好用了？

A：线性回归解决这类问题的方法是拟合后设置阈值，再区分成离散值。

如图，当在远处值，拉低了直线的斜率，就会让前面的肿瘤被误判成0.

（别忘了 x₀ 默认为1，以此让 θ₀作为偏移量，让直线离开原点）

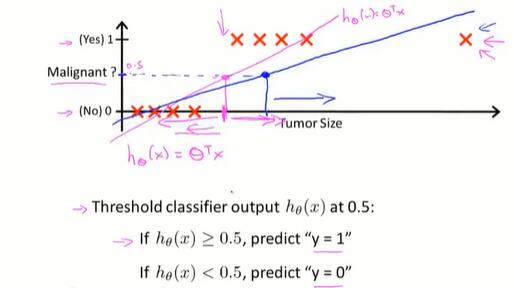
另外，与linear regression不同，logistic regression算法需要让 $h_\theta(x)$ 的值在 [0, 1]。

6.2 假设表示（hypothesis representation）

当有一个分类问题，我们要用哪个方程，来表示我们的假设？

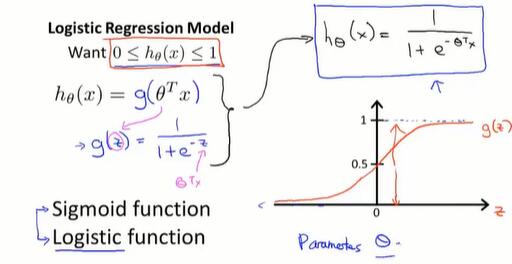
Sigmoid/Logistic 方程如图，我们通过拟合出 θ，让 x 和 h 反应真实情况。

从结果上，我们的结论是 $h_\theta(x)=P(y=1|x;\theta)$ ，即：x 这个样本，有 h 的概率，是 y=1 代表的情况.

（” probability that y = 1, given x, parameterized by θ “）

6.3 判定边界（decision boundary）

这个概念让我们理解假设函数 h 是如何做出预测的。

当 $\theta^Tx ≥ 0$ 时，有 $h_\theta(x) = g(\theta^Tx) ≥ 0.5$ ，取离散值 y = 1；
当 $\theta^Tx ≤ 0$ 时，有 $h_\theta(x) = g(\theta^Tx) ≤ 0.5$ ，取离散值 y = 0。

一个例子：

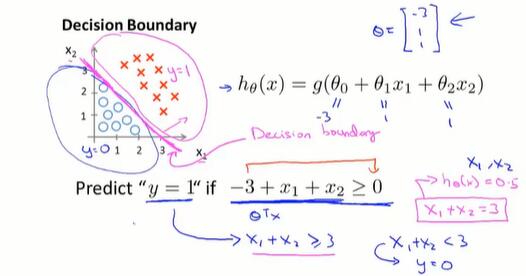
以上图两个x的情况为例，$\theta$ 可以确定一条直线，把 y = 1 和 y = 0 的情况分隔开，这条直线就叫判定边界。

在 4.5 节中介绍了多项式回归，在特征 x 中，添加额外的高阶多项式项。在逻辑回归中也适用：

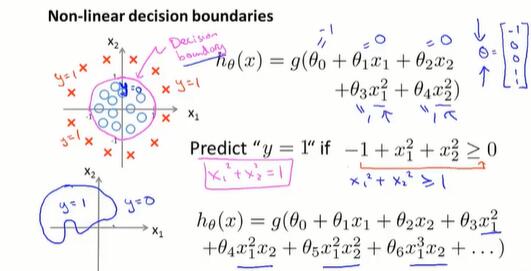
区别是线性回归改的是 $h_\theta(x) = \theta^Tx$，而逻辑回归问题改的是 $\theta^Tx$ ， $h_\theta(x) = g(\theta^Tx)$。

需要注意的是：判定边界是由 θ 确定的，不是由训练集定义的。训练集的 x 所做的只是拟合出合适的 θ。

问题来了：如何根据数据，自动拟合出参数 θ ？（有些包的函数可以，如scipy）

6.4 代价函数（cost function）

问题如下：如何选择 θ ？该定义怎样的代价函数来迭代 θ ？

在线性回归问题中，$h_\theta(x)=\theta^Tx$ 是线性函数，定义 $Cost(h_\theta(x), y) = \frac{1}{2}(h_\theta(x)-y)^2$ ，进而定义代价函数 $J(\theta) = \frac{1}{m} \Sigma Cost$。$J(\theta)$是 convex 函数，梯度下降可以应用。

而在逻辑回归问题中， $h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}$ 不是线性的，如果还是像线性回归那样计算 $J(\theta)$ ，会发现 $J(\theta)$ 是一个 non-convex 函数，使梯度下降无法应用。

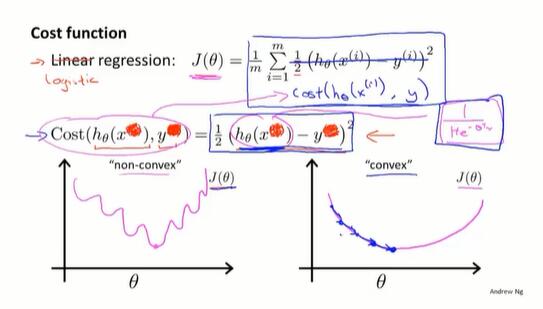
需要另外找一个是凸函数的Cost函数：

$$ Cost(h_\theta(x), y)= \begin{cases} -log(h_\theta(x)),&\text{if } \quad y=1 \\ -log(1-h_\theta(x)),&\text{if } \quad y=0 \end{cases} $$

y = 1 时，预测出的 h 越偏离 1，Cost 越大；

y = 0 时，预测出的 h 越偏离 0，Cost 越大。

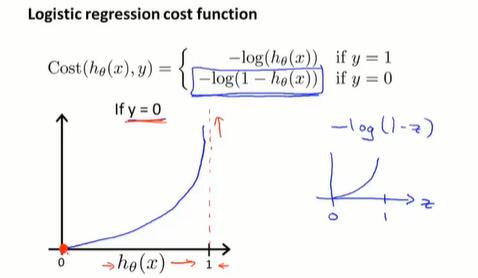
本节定义了单训练样本的代价函数，虽然没有进行详细的凸性分析，但代价函数此时是凸函数。接下来将扩展此结论，给出整个训练集的代价函数的定义。并给出更简单的写法。

6.5 简化代价函数和应用梯度下降

简化代价函数：

逻辑回归的代价函数：

$$J(\theta) = \frac{1}{m}\sum_{i=1}^{m}Cost({h_\theta(x^{(i)}), y^{(i)}})$$

$$\begin{equation} Cost(h_\theta(x), y)=\left\{ \begin{array}{rcl} -log(h_\theta(x)) & \text{if} \quad y=1\\ -log(1-h_\theta(x)) & \text{if} \quad y=0\\ \end{array} \right. \end{equation}$$

$$Note:y总是取0或1$$

Cost函数简写为：

$$Cost(h_\theta(x), y)= -y \log h_\theta(x)-(1-y) \log(1-h_\theta(x))$$

代价函数简写为：

$$J(\theta) = -\frac{1}{m}[\sum_{i=1}^{m}y^{(i)} \log h_\theta(x^{(i)})+(1-y^{(i)}) \log(1-h_\theta(x^{(i)}))]$$

Q：为什么选择这样形式的代价函数？

A：虽然没有详细解释，但这个式子是通过极大似然法得来的，是统计学中，为不同的模型快速寻找参数的方法。并且这是一个convex函数。

应用梯度下降：

（todo：↑ 上式少写了一个 $\frac{1}{m}$？）

从形式上，逻辑回归和线性回归的梯度下降表达式一样。但两者的 $h_\theta(x)$ 定义不同，实际上是完全不同的东西。

在线性回归介绍的方法，像如何监控梯度下降正常运行、feature scaling 在逻辑回归也适用。

6.6 高级优化

除了梯度下降，还有其他的高级算法能让 $J(\theta)$ 收敛。如共轭梯度、BFGS、L-BFGS。

只需知道用法即可，不一定要弄清所有的实现细节，也不要自己去实现这些算法。

function [jVal, gradient] = costFunction(theta)
	jVal = (theta(1) - 5) ^ 2 + (theta(2) - 5) ^ 2;
	gradient = zeros(2, 1);
	gradient(1) = 2 * (theta(1) - 5);
	gradient(2) = 2 * (theta(1) - 5);

options = optimset('GradObj', 'on', 'MaxIter', '100');
initialTheta = zeros(2, 1)
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options)

以上代码调用 fminunc 来进行函数的收敛和 optTheta 的迭代。

对于一般场景的逻辑回归，多个theta的处理方式如下：

6.7 多分类问题：一对多（multi-class classification）

训练集的数据有多个分类，如何拟合分类器？

one-vs-all 方法：把训练集的每个类别分别单独拟合一个分类器。

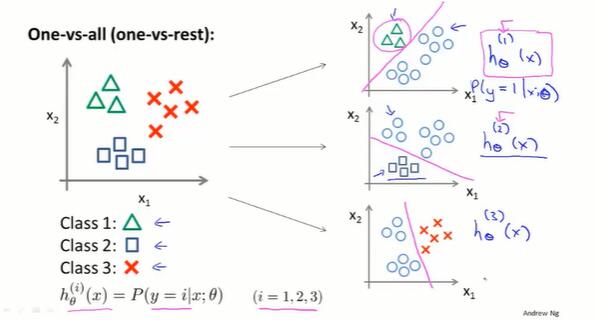
训练一个逻辑回归分类器 $h_\theta^{(i)}(x)$ ，对于每个类别 $i$ ，分类器预测 $y = i$ 的概率。

为了预测任意一个输入 $x$ 的分类，取 $\max i: h_\theta^{(i)}(x)$ ，即让分类器取最大概率值的 $i$ 类别。

第七章正则化（Regularization）

7.1 过拟合问题（overfitting）

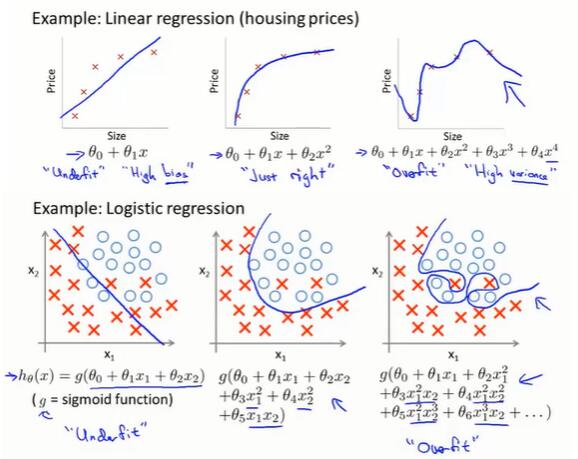
过拟合（overfit）：过于贴近训练数据的特征了，在训练集上近乎完美的预测/区分了所有的数据，但是缺乏泛化能力，在新的测试集上表现不佳。
欠拟合（underfit）：测试样本的特性没有学习到，或模型过于简单无法拟合或区分样本。

(识别过拟合、欠拟合的情况。)

当 features 的数量太多，甚至比 training data 的数量都多，就很有可能出现过拟合。比如像窗户的数量、门的数量等特征，看上去都与房屋的价格有关。

解决过拟合问题的方法：

减少特征的数量
- 人工选择特征，进行取舍。舍弃特征的同时也会舍弃信息。
- 使用模型选择算法，自动选择保留的特征。（在之后介绍）
正则化（regularization）
- 保留所有特征，但减少参数 $\theta_j$ 的量级/大小。
- 情况：有多个特征、并且每个特征都是或多或少有用的，我们不希望把他们舍弃掉。

7.2 正则化的直观理解、代价函数（cost function）

正则化的直观理解：

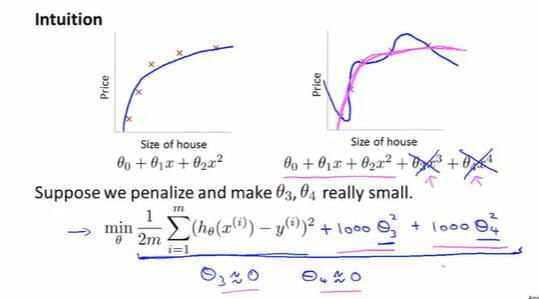
通过减小参数 θ₃、θ₄ 的值，给 x₃、x₄ 两个特征加入惩罚，曲线就跟二次函数没什么区别了。

这就是正则化背后思想：

不知道具体哪些特征 x 该舍弃掉，就减小所有参数 θ 。

具体方法

在 $J(\theta)$ 后面加上一项 $\lambda\sum^{n}_{i=1}\theta_j^2$ ，在收敛 $J(\theta)$ 的同时让所有 $\theta$ 变小。

tips：

通常不含常数项 $\theta_0$ ，但影响不大。
要选择合适的正则化参数 $\lambda$。$\lambda$ 的作用是在两个目标中平衡：表达式前面的项代表对数据更好的拟合，后面的项代表让参数尽量小来避免过拟合。
- $\lambda$ 越大，$\theta$ 的惩罚越大。如果 $\lambda$ 太大，$\theta$ 都接近0，就相当于把假设函数的项都忽略掉了，最后只剩一个常数项 $\theta _0$，造成欠拟合。

(问题：如何自动选择 $\lambda$ ？)

7.3 线性回归的正则化（regularized linear regression）

拟合线性回归模型的两种算法：基于梯度下降、基于正规方程。

梯度下降

在 $J(\theta)$ 的最后加一项 $\frac{\lambda}{2m}\sum^n_{j=1}\theta^2_j$ 。

梯度下降，求偏导 $\frac{\lambda}{m}\theta_j$ ：

直观的理解，正则化的梯度下降是让 $\theta_j$ 每次额外乘以一个比1略小的数 $(1-\alpha\frac{\lambda}{m})$ ，每次都把参数改小一点。

将 θ₀ 和其余 θ 区别开。（$(1-\alpha\frac{\lambda}{m})$ 跟1差不多大，所以区分开的影响不大。可以对比两个式子看正则化给梯度下降带来的变化。）

正规方程

回忆一下正规方程：构造 m*(n+1) 矩阵 X 和 m 维向量 y ，设定代价函数的导数为 0，用最小二乘法计算 θ。

正规方程正则化的方式是加一个 (n+1)*(n+1) 的方阵，这个方阵的构造如下图所示。

*正则化中的 $X^TX$不可逆问题（见4.7）：

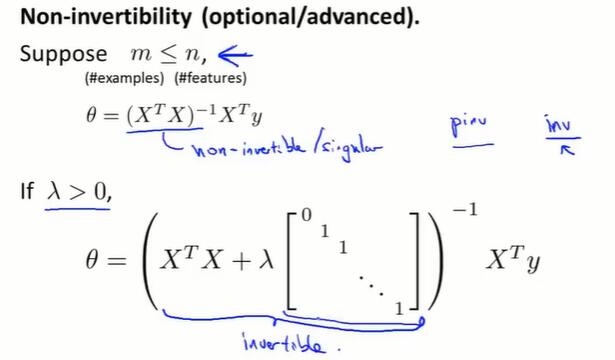
在不进行正则化时，一些语言的库函数也可以计算不可逆的矩阵。

进行正则化后，如果 $\lambda>0$ ，可证得 $(X^TX+\lambda R)$ 一定是可逆的。

7.4 逻辑回归的正则化（regularized logistic regression）

跟线性回归的梯度下降差不多。

在 $J(\theta)$ 的最后加一项 $\frac{\lambda}{2m}\sum^n_{j=1}\theta^2_j$ 。

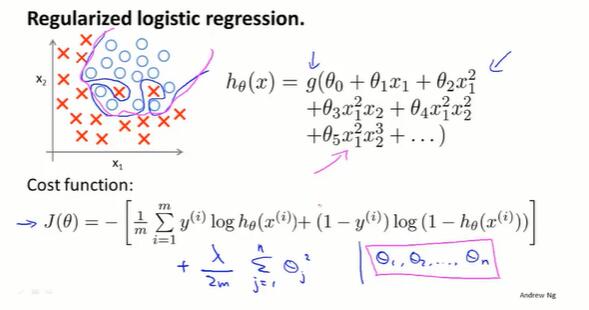
梯度下降求偏导 $\frac{\lambda}{m}\theta_j$ ：

实现方法：先定义代价函数：

再把代价函数用到fminunc：fminunc(@costFunction); 。

第八章神经网络：表述（Neural Networks: Representation）

8.1 非线性假设

Q：为什么要学习神经网络算法？（跟线性回归、逻辑回归相比有什么先进性）

A：如果n太大，feature太多，之前介绍的算法就不理想了。对于许多实际的机器学习问题，n一般是很大的。

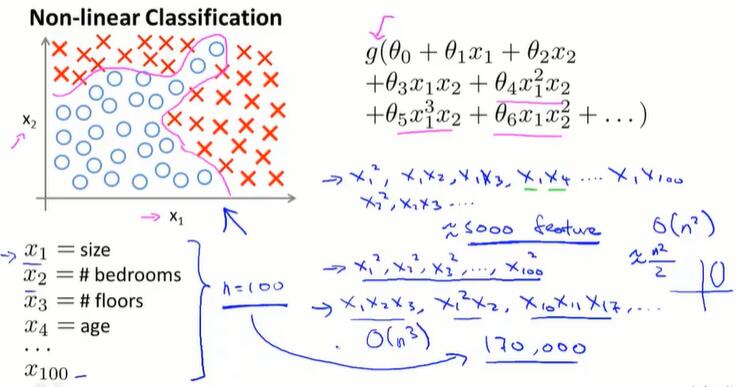
如图，100个n会产生约5000个二次项，对应同样多的参数。如果包含所有的二次项，运算量会很大，并且很可能会出现过拟合的现象。如果再包含三次项，……。当n很大，通过增加feature来建立非线性分类器不是一个好办法。

而现实中的问题往往有很大的n。如50*50分辨率的灰度图像，要存储每个像素的值，n=50*50=2500；进行特征映射，n=2500*2500/2≈3,000,000。

8.2 神经元和大脑

可以用单个算法来模拟大脑的学习算法吗？

本节课举例论证了：人的一些感官是相通的——可以把任何sensor接入大脑，然后大脑的学习算法就能找出学习数据的方法，并处理这些数据。

现在的问题：如何找出大脑的学习算法？

8.3 模型表示Ⅰ

当使用神经网络时，如何表示我们的假设或模型？大脑里的神经元是相互连接的，通过接收、处理、传递电信号的方式工作。

通过以下方式表示单个的人工神经元：

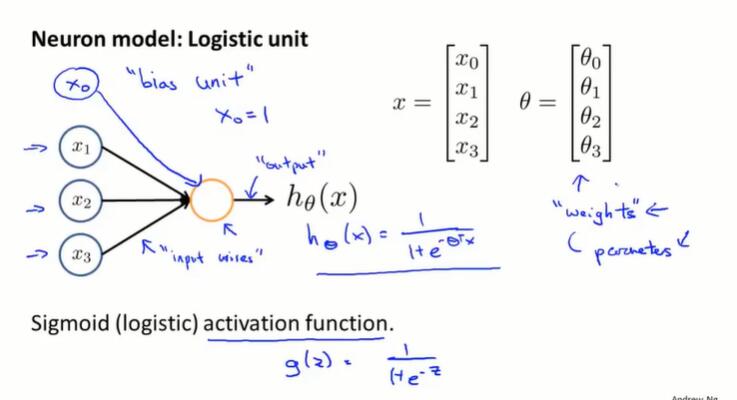
模型的表示：

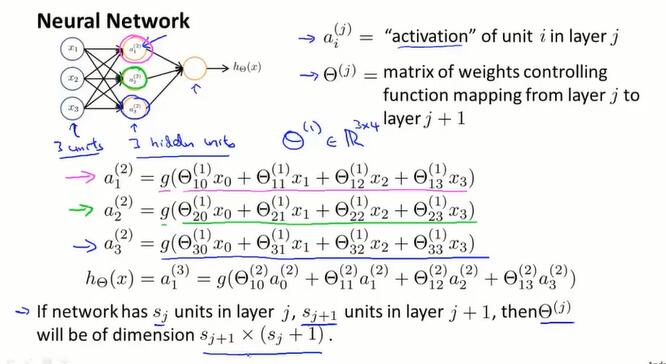
用 $a_i^{(j)}$ 表示第 $j$ 层的第 $i$ 个神经元。
用 $\Theta^{(j)}$ 表示从第 $j$ 层到 $j+1$ 层的权重矩阵。
如果一个网络，在第 $j$ 层有 $s_j$ 个单元，在第 $j+1$ 层有 $s_{j+1}$ 个单元，那么 $\Theta^{(j)}$ 的维度是 $s_{j+1}×(s_j+1)$。是从后往前的形式。
- 我的理解：矩阵的行是下一层的每个神经元的权重列表，列对应上一层的神经元。列要加一是加上上一层的偏置，也就是$x_0$。

8.4 模型表示Ⅱ：向量化和前向传播

本章直观地理解向量化的方法，并明白为什么这是学习复杂的非线性假设函数的好方法。

向前传播的向量化：

$z^{(j+1)} = \Theta^{(j)}a^{(j)}$，每层的 $z:(s_{j+1}×1)$ 是偏置矩阵 $\Theta:(s_{j+1}×(s_j+1))$ 和上层的输出 $a:((s_j+1)×1)$ 做矩阵运算得出的。
$a^{(j)} = g(z^{(j)})$，每行的输出 $a$ 是对 $z$ 做 sigmoid 运算。
每一层都添加偏置 $a_0^{(j)}=1$

这种前向传播的方法也可以帮助我们了解神经网络的作用，和神经网络算法为什么能在学习非线性假设函数时有好的表现。

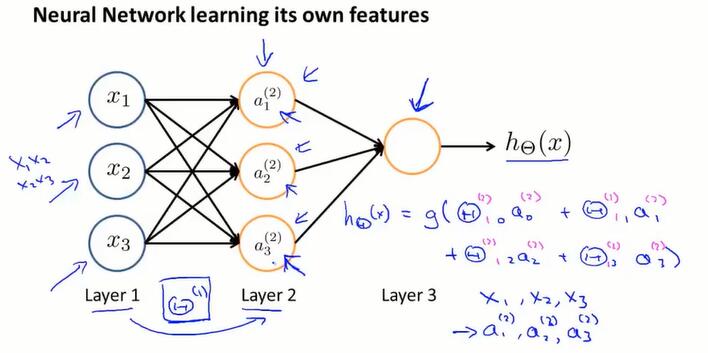
神经网络在每一层都像是做一个逻辑回归，根据输入拟合一些权值；而且每层的输入都是前层根据自动拟合的权值，计算得到的输出，因此可以包含一些很复杂的特征。神经网络可以利用隐藏层计算更复杂的特征，并最终输出到输出层。

在接下来的两章，讨论具体的例子，描述如何利用神经网络来计算输入的非线性假设函数。

8.5 举例直观理解Ⅰ

使用神经网络计算 AND 门：

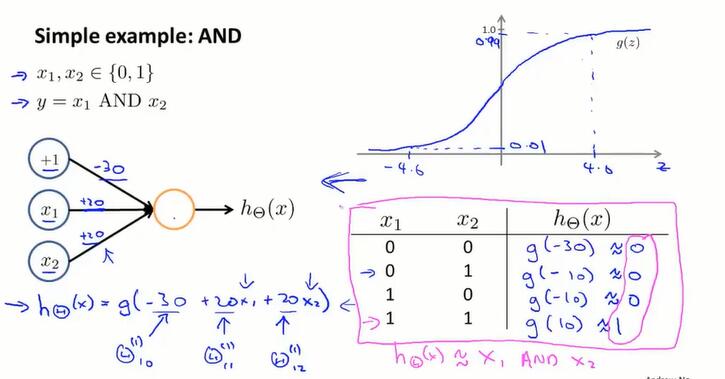
计算 OR 门：

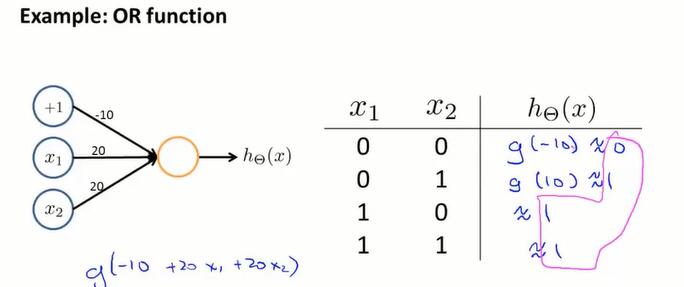
只要设置恰当的权值，神经网络就能起到相应的作用。

8.6 举例直观理解Ⅱ

使用感知机来解决非线性问题：亦或。

使用有一层隐藏层的神经网络计算 NOR 函数：

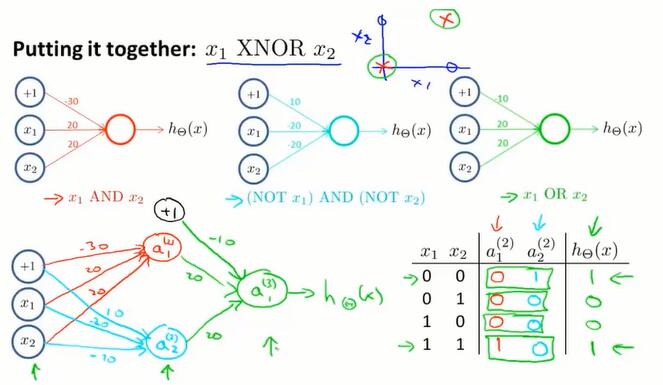
x₁ NOR x₂ = (x₁ AND x₂) OR ( (NOT x₁) AND (NOT x₂) )

通过识别手写数字的视频展示了，神经网络可以学习相当复杂的函数，并且有一定的抗干扰能力：

8.7 神经网络的多元分类问题（multi-class clasification）

上节的手写数字识别问题就是多分类问题，需要识别10种类型的数字。

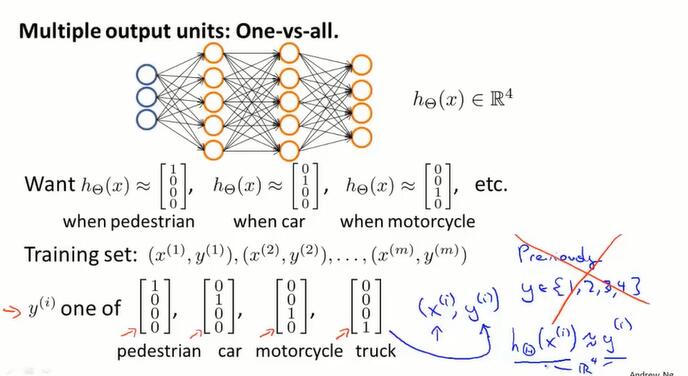
方法是设置多个输出层神经元，再把训练集 $(x^{(i)},y^{(i)})$ 、输出 $h_\Theta(x^{(i)})=y^{(i)}$ 的 $y$ 都变成向量的形式。途中输出分成四类，则 $y$ 是四维向量。

本章讲述了如何构建模型来表示神经网络算法。在下一章，将学习如何构建训练集，如何让神经网络自动学习参数。

第九章神经网络的学习（Neural Networks: Learning）

讲一个学习算法，可以在给定数据集上，为神经网络拟合参数。

9.1 代价函数（cost function）

神经网络的符号表示：

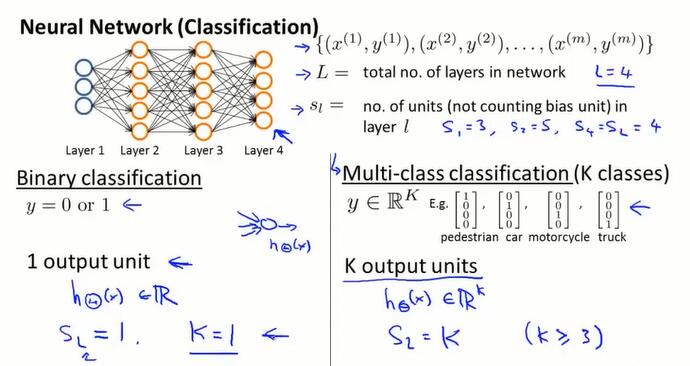
$L$：层数
$s_l$：第 $l$ 层的神经元数（不含偏置神经元）
$K$：输出神经元的个数。
- 二元神经网络的 $s_l=K=1$，多元神经网络的 $s_l=K$。
- $h_\Theta(x) ∈ \R^K$

神经网络的代价函数：

逻辑回归的代价函数一般表达式如下：

$$J(\theta) = -\frac{1}{m}\bigg[\sum_{i=1}^{m}y^{(i)} \log h_\theta(x^{(i)})+(1-y^{(i)}) \log(1-h_\theta(x^{(i)}))\bigg]+\frac{\lambda}{2m}\sum_{j=1}^n\theta^2_j$$
对于神经网络，有

$$h_\Theta(x)∈\R^K,(h_\Theta(x))_i=i^{th} output$$

$$ J(\Theta) = -\frac{1}{m}\bigg[\sum_{i=1}^{m}\sum_{k=1}^{K}y^{(i)}_k \log (h_\Theta(x^{(i)}))_k+(1-y^{(i)}_k) \log(1-h_\Theta(x^{(i)}))_k\bigg] \\ +\frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_{l+1}}(\Theta^{(l)}_{ji})^2 $$

与逻辑回归的代价函数不同点在于：

把 K 个输出神经元的损失加起来，再求 m 个数据上的平均
正则化项，取所有边权重的平方和。i 从1开始，不含偏移神经元的权重。

9.2 反向传播算法（backpropagation algorithm）

一个让上节的损失函数取到最小值的算法

上节定义了 $J(\Theta)$，如果想让 $J(\Theta)$ 取到最小值，就需要计算 $\frac{\partial}{\partial\Theta^{(l)}_{ij}}J(\Theta)$

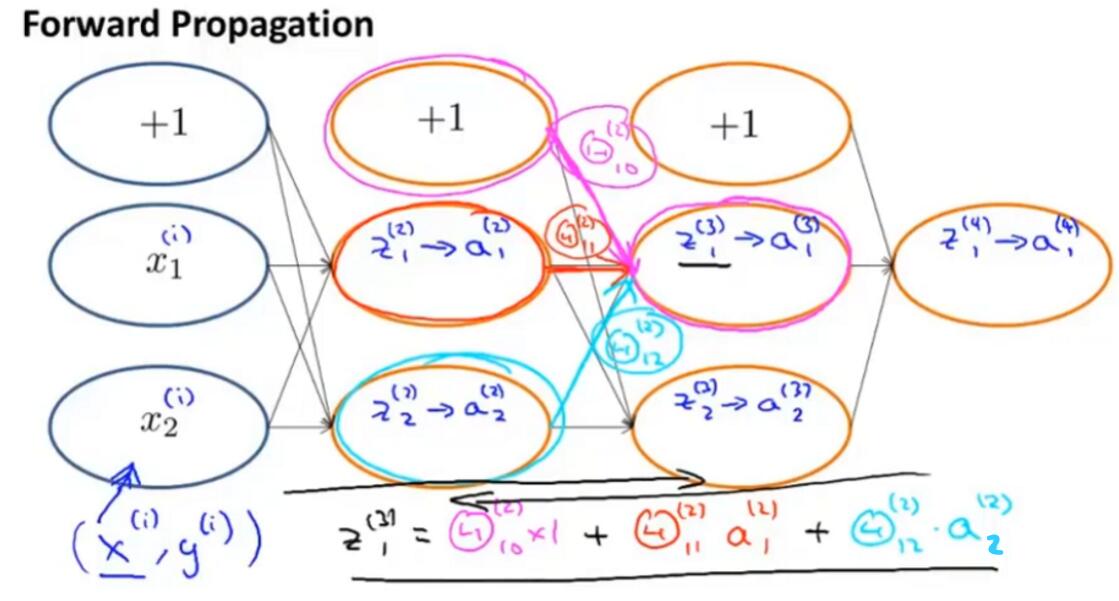
首先来看前向传播的向量化：

此处可以仔细理解一下前向传播的计算过程。

以上图为例，如果只有一组数据集 $(x, y)$，
$a^{(1)}$的规格是 3×1，$\Theta^{(1)}$的规格是 5×3，
向量化后相乘，得到 $z^{(2)}$的规格是 5×1，求sigmoid后加一个偏移项则 $a^{(2)}$的规格是 6×1，
$\Theta^{(2)}$的规格是 5×6，相乘得到 $z^{(2)}$的规格是 5×1，
以此类推。使用前向传播，可以从输入，通过神经网络，得到输出。

回到主题，为了计算导数项 $\frac{\partial}{\partial\Theta^{(l)}_{ij}}J(\Theta)$，需要使用反向传播算法：

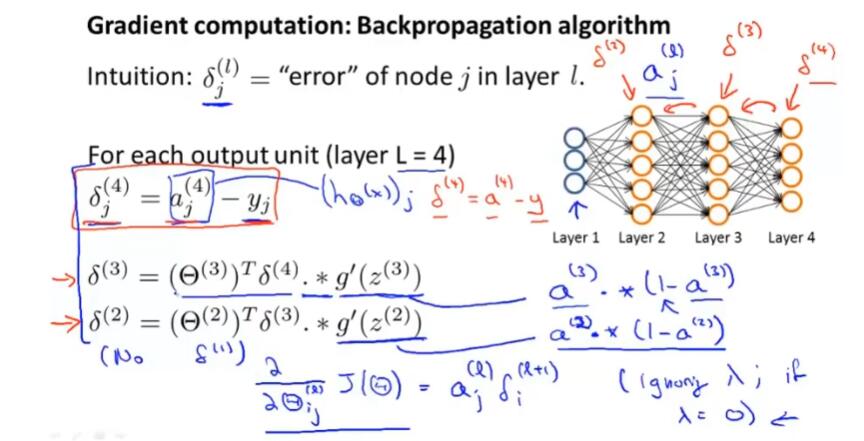
对于每一个节点，我们计算这样一项 $\delta^{(l)}_j$，代表了第 $l$ 层第 $j$ 个节点的“误差”
从输出层，反向计算每层的误差。
然后，根据 $\frac{\partial}{\partial\Theta^{(l)}_{ij}}J(\Theta) = a^{(l)}_j\delta^{(l+1)}_i$（此式省略了 $\lambda$ 等参数），可以求得想要的偏导数。

反向传播算法的整体过程

有训练集 ${( x^{(1)},y^{(1)} ),…,(x^{(m)},y^{(m)}) }$
设置初始误差矩阵 $\Delta^{(l)}_{ij}=0$，保存整个神经网络的误差
For $i=1$ to $m$ ：
- 设置输入层 $a^{(1)}=x^{(1)}$
- 进行前向传播，求每层输出 $a^{(l)}$
- 使用 $y^{(i)}$ ，计算输出层的误差 $\delta^{(L)} =a^{(L)}-y^{(i)}$
- 进行反向传播，计算每层误差 $\delta^{(L-1)},\delta^{(L-2)},…,\delta^{(2)}$
- 累加误差矩阵 $\Delta^{(l)}_{ij}:=\Delta^{(l)}_{ij}+ a^{(l)}_j\delta^{(l+1)}_i$
计算 $D$
- $D^{(l)}_{ij}:=\frac{1}{m}\Delta^{(l)}_{ij}+\lambda\Theta^{(l)}_{ij}$，if $j ≠0$
- $D^{(l)}_{ij}:=\frac{1}{m}\Delta^{(l)}_{ij}$ ，if $j =0$
$\frac{\partial}{\partial\Theta^{(l)}_{ij}}J(\Theta) = D^{(l)}_{ij}$ ，求得偏导
使用偏导进行梯度下降，或其他高级优化算法

补充：

反向传播不用计算 $\delta^{(1)}$ ，因为不需要对输入层考虑误差项。
累加误差矩阵写成向量相乘形式： $\Delta^{(l)}_{ij}:=\Delta^{(l)}_{ij}+ \delta^{(l+1)}_i(a^{(l)}_j)^T$

9.3 反向传播算法的直观理解

前向传播的直观理解：

反向传播的直观理解：

可以把神经网络的代价函数中的主要部分，类比为线性回归的代价函数的方差计算。只需明确：本质上做的是“求与真实值y的偏离程度”这件事。

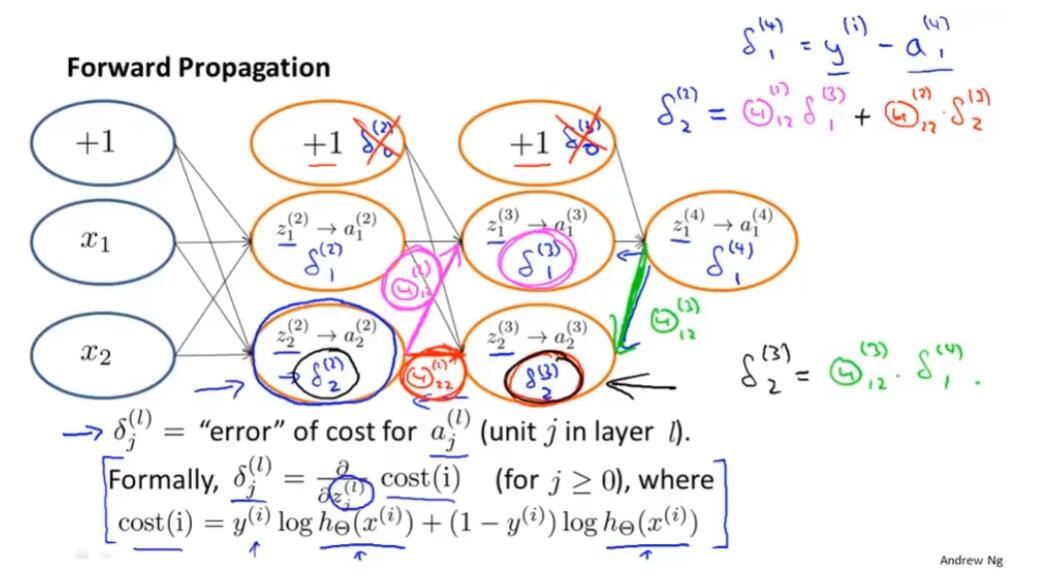
而反向传播过程中，计算的 $\delta_j^{(l)}$ 就是 cost 关于 z 的偏导数。具体来说，cost 是一个关于真实值 y 和神经网络的输出值 h(x) 的函数。 $\delta_j^{(l)}$实际上是 cost 关于这些计算出的中间项的偏导数。$\delta_j^{(l)}$衡量的是，为了影响这些中间值 z （进而影响整个神经网络的输出 h），我们想要改变的神经网络的权重的程度。

9.4 使用注意：展开参数

怎样将参数从矩阵展开成向量，以满足高级最优化步骤中的使用需要

如上图，定义一个代价函数 costFunction，输入参数是 theta，函数返回代价值 jVal 以及导数值（梯度） gradient。

然后将这个函数传递给高级最优化算法 fminunc，这些库函数都假定 theta、initialTheta 是参数向量，同时假定代价函数的第二个返回值，也就是梯度值 gradient 也是一个向量。

这部分在我们使用逻辑回归的时候没有问题，但在神经网络中，参数矩阵 $\Theta$ 和梯度矩阵$D$ 都是矩阵而非向量，因此需要将这些矩阵展开成向量，从而作为参数输入到函数中。

以上图 Octave 语言为例：

首先有初始参数值矩阵 $\Theta$ ，将他们展开成向量 initialTheta，传递到高级优化函数 fminunc 中。
使用 fminunc 函数需要事先定义 costFunction 函数，它的参数是 thetaVec，所有的参数展开成一个向量的形式。因此需要做的第一件事就是用 reshape 功能将 thetaVec 转换成参数值矩阵 $\Theta$，然后才能进行前向、反向传播，来计算导数 $D$ 和计算代价函数 $J(\Theta)$。最终，将 $D$ 展开成向量，得到需要返回的梯度向量 gradientVec。

一般是用 reshape() 函数来进行矩阵、向量形式的转换。

用矩阵存储的好处：更方便进行正向、反向传播。
用向量存储的好处：一些高级优化算法要求参数要展开成一个长向量的格式。

9.5 梯度检验（gradient checking）

前面几节讲了怎样在神经网络中进行前向、反向传播，来计算导数。但反向传播算法很难实现，并且在执行上可能出现一些bug，比如 $J(\Theta)$ 减小但最终得到的神经网络误差很大。

梯度检验思想能解决几乎所有这种问题，能完全保证前向、反向传播算法是百分百正确的。在使用反向传播的场合中，最好做一下梯度检验。

第一步：估算导数

当 $\Theta$ 是实数：

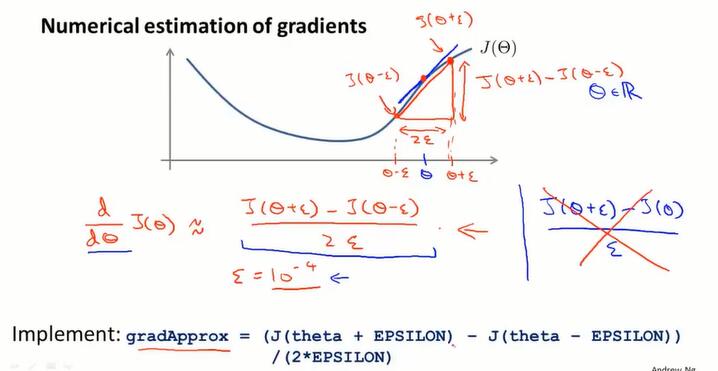
在数值上去拟合 $J(\Theta)$ 的导数：

$$ \frac{d}{d\Theta}≈\frac{J(\Theta+\epsilon)-J(\Theta-\epsilon)}{2\epsilon} $$

当 $\Theta$ 是向量：（比如是从矩阵展开而来的）

在Octave的实现：

for i = 1:n,
	thetaPlus = theta;
	thetaPlus(i) = thetaPlus(i) + EPSILON;
	thetaMinus = theta;
	thetaMinus(i) = thetaMinus(i) - EPSILON;
	gradApprox(i) = (J(thetaPlus) - J(thetaMinus)) / (2 * EPSILON);
end;

用 gradApprox 来近似计算 $\frac{\partial}{\partial\Theta_i}J(\Theta)$

第二步：对比估算值和反向传播的结果

检查 gradApprox ≈ Dvec

DVec 是反向传播得出的导数矩阵。检查估算的 gradApprox 是否在数值上跟反向传播算法计算出的导数接近。

总体实现过程：

在第三步中，如果估计值和反向传播的结果在数值上近似，那么第四步，就把梯度检验关掉，不要再计算估计值 gradApprox 了，使用反向传播的结果来进行神经网络的学习。

原因是近似求导计算 gradApprox 是计算量非常大、耗时、不稳定的。而计算 DVec 的反向传播算法是高性能的求导方法（仅向量计算）。

9.6 随机初始化（random initialization）

如何初始化 $\Theta$ ？

在逻辑回归中，可以将初始参数都设置为 0 .但在训练网络时，将 0 作为初始值起不到任何效果：

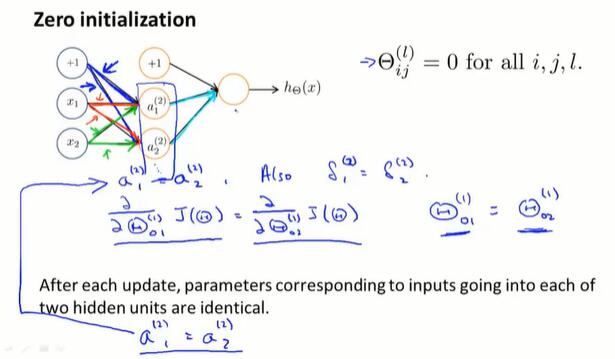
由于权重是相同的（都是0），在前向传播中，同层的节点将会得到相同的输出值；而在反向传播中，也会得到相同的导数值。如图，相同颜色的边会得到相同的权值、偏导。这被称为“对称权重问题（symmetric weights）”

为了解决这个问题，使用随机初始化的思想，进行 symmetry breaking。

rand取 [0,1]，(2*rand - 1)*EPSILON 取 [-EPSILON, EPSILON].

综合前几节，训练神经网络的过程如下：

随机初始化权重于 $[-\epsilon,\epsilon]$
进行反向传播
进行梯度检验
使用梯度下降或其他高级优化算法，最小化 $J(\Theta)$
得出 $\Theta$ 的最优值

9.7 组合起来

训练神经网络

确定一个网络结构
- 输入层单元的个数：数据集中 $x^{(i)}$ 特征的维度
- 输出层单元的个数：分类的个数
  - 对于分类问题，要记得把输出 y 写成向量的形式，其中有一项 1 表示哪一类，剩下都为0.
- 隐藏层如何设计：
  - 一个合理的默认选项是使用一个隐藏层。
  - 使用多个隐藏层时，每层的隐藏单元数量相同。（通常越多越好，但要注意计算量问题）
需要实现的步骤
- ① 随机初始化权重
- ② 实现前向传播算法，计算每条数据 $x^{(i)}$ 经过神经网络得到的输出 $h_\Theta(x^{(i)})$
- ③ 实现损失函数 $J(\Theta)$
- ④ 实现反向传播算法，计算偏导 $\frac{\partial}{\partial\Theta^{(i)}_{jk}}J(\Theta)$
  - 使用一个循环 for i = 1:m 来进行前向传播和反向传播，对于数据集中的每条数据 $(x^{(i)},y^{(i)})$ 计算每层的 $a^{(l)}$ 和 $\delta^{(l)}$ ；然后在循环中更新 $\Delta^{(l)}$
- ⑤ 实现梯度检验，对比反向传播的结果 $\frac{\partial}{\partial\Theta^{(l)}_{jk}}J(\Theta)$ 和数值上的估计值。然后禁用梯度检验的代码。
- ⑥ 使用梯度下降算法，跟反向传播结合，最小化 $J(\Theta)$，得到最终权重 $\Theta$

直观理解

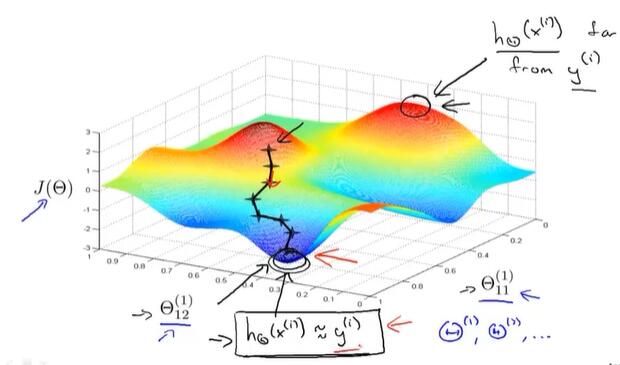
如下图，① 随机选取一个起始点，④ 反向传播算出梯度下降的方向，⑥ 梯度下降就是沿着这个方向一点点下降，知道到达局部最优点。

9.8 无人驾驶

一个有趣并具有历史意义的神经网络学习的例子：实现自动驾驶

左上方第一个白条显示人类驾驶员选择的方向，第二、三个白条显示两个网络的置信度、以及学习算法选择的行驶方向。

刚开始随机初始化后，输出整段模糊的灰色区域，学习后才集中到一块白亮的小区域，选择明确的驾驶方向。

左下方显示前方景象。

这个任务基于三层的神经网络，使用反向传播算法。数据集是压缩后的前方图片和驾驶员选择的方向。

训练完成后，每秒钟生成12张数字化的图片，传送给神经网络进行计算，使用输出进行自动驾驶。

分为单行道网络、双车道网络，分别计算置信度（confidence），根据不同的路况，置信度高的网络就被选择来控制行驶方向。

第十章应用机器学习的建议(Advice for Applying Machine Learning)

给出一些建议，当在开发一个机器学习系统时，如何决定该选择哪条道路。

10.2、10.3讲怎样评估机器学习算法的性能，10.4、10.5讲机器学习诊断法。

10.1 决定下一步做什么

Debugging a learning algorothm：

假设已经实现了正则化的线性回归，得到用来预测房价的模型：

$$ J(\theta) = \frac{1}{2m}\bigg[\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2 + \lambda\sum^m_{j=1}\theta^2_j\bigg] $$

然而，当在训练集上测试得到的参数时，我们发现预测的结果有很大的误差。我们应该如何改进？

收集更多的训练样本（在有些时候没有效果。在之后的章节会将如何避免把过多时间浪费在收集样本上）
尝试使用更少的特征
尝试获取更多特征，来收集更多的数据
尝试增加多项式特征（$x^2_1,x^2_2,x_1x_2,etc.$）
尝试增加/减小 $\lambda$

大多数人的方法是，随便从这些方法中选择一种，然后花很长时间检验这种方法是否有效。

有一种简单的方法，可以轻松地排除掉一些选项：机器学习诊断法（machine learning diagnostic）。我们可以使用诊断法，明确在机器学习算法中，什么有效什么无效，并且可以获得如何提升性能的指导。

10.2 评估一个假设

如何评估学习算法得到的假设。基于这一节，在之后会讲如何防止过拟合和欠拟合的问题。

我们获得学习算法的方式是让代价函数取最小，但会产生过拟合假设的问题。当在特征少的情况下，我们可以通过函数图像发现过拟合现象，但当特征多时，函数难以可视化，我们需要另一种评价假设函数的方法。

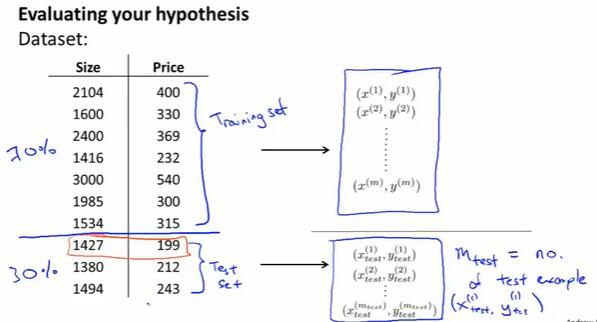
把数据集随机分为训练集和测试集。数量上 7:3 是比较常见的分法。

一种典型的训练、测试线性回归的方法：

在 70% 占比的训练集上学习 $\theta$（最小化误差函数$J(\theta)$）
计算出测试误差：$J_{test}(\theta) =\frac{1}{2m}\sum^{m_{test}}_{i=1}(h_\theta(x^{(i)}_{test})-y^{(i)}_{test})^2$

训练、测试逻辑回归：

在训练集上学习 $\theta$
在测试集上计算测试误差，有两种定义方法：
- 计算逻辑回顾误差：$J_{test}(\theta) = -\frac{1}{m_{test}}\sum^{m_{test}}_{i=1}y_{test}^{(i)}\log h_{\theta}(x^{(i)}_{test})+(1-y_{test}^{(i)})\log h_{\theta}(x^{(i)}_{test})$
- 错误分类误差（0/1 misclassification erorr）：详见图。

10.3 模型选择和交叉验证集

如何评估学习算法：模型选择问题。

对于一个数据集，最合适的多项式次数如何确定；怎样选择合适的特征来构造学习算法；如何确定学习算法的正则化参数 $\lambda$

模型选择Ⅰ

一种选择模型的方法：在多种特征的选择方法中，分别进行训练得出 $\Theta$，然后分别在测试集上进行测试，然后从这些模型中选出表现最好的一个（ $J_{test}(\Theta^{(i)})$ 最小）。

问题：判断这个模型的泛化能力如何？

我们可以观察这个假设模型对测试集的拟合情况，但问题是，这样做仍然不能公平地估计出这个假设的泛化能力。原因：参数 d 是多项式的次数（特征的维度），我们用测试集拟合了参数 d，选择了能够最好地拟合测试集的参数 d 的值。我们的参数向量 $\Theta$ 在测试集上的性能很可能是对泛化误差过于乐观的估计。也就是说，测试集的误差 $J_{test}$ 让我们找出了最好的模型，但不能用同一个误差来衡量模型的泛化能力。

交叉验证集

将数据分为三部分：训练集60%（training set）、交叉验证集20%（cross validation set）和测试集20%（test set）。

模型选择Ⅱ

对于每种模型，训练出 $\Theta$，然后在交叉验证集上计算 $J_{cv}(\Theta)$，选择表现最好的参数 d，即选择某个模型。在测试集上进行误差的估计，计算 $J_{test}(\Theta)$，就可以用 $J_{test}(\Theta)$ 来衡量算法选出的模型的泛化能力了。

10.4 诊断偏差和方差（diagnosing bias vs. variance）

当一个模型表现不好，主要有两种原因：高偏差（high bias，欠拟合）、高方差（high variance，过拟合）。

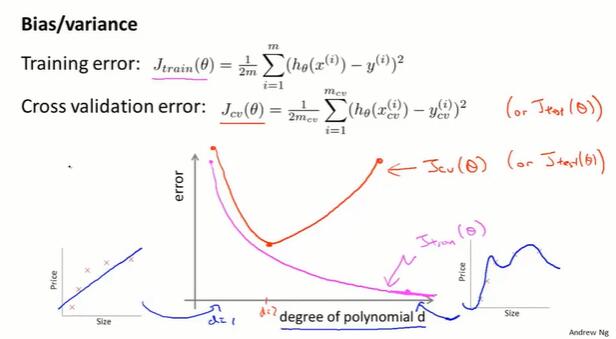
多项式次数小，训练集上表现不佳，bias高。
多项式次数高，训练集上拟合得好，bias低；但交叉验证集上会过拟合，variance高。

如何确定模型为何表现不佳？

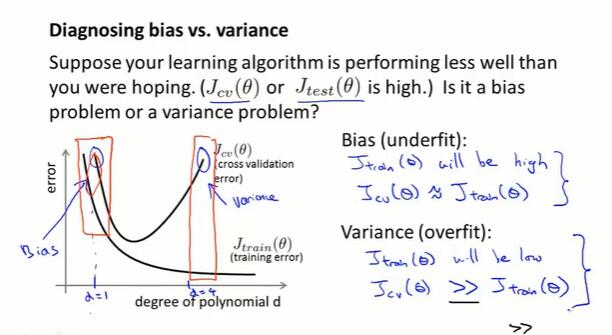
Bias（欠拟合）：
- 训练集上表现不好，$J_{train}(\Theta)$ 高
- 交叉验证集上表现不好，$J_{cv}(\Theta)≈J_{train}(\Theta)$
Variance（过拟合）：
- 训练集上表现很好，$J_{train}(\Theta)$ 低
- 交叉验证集上表现不好，$J_{cv}(\Theta)>>J_{train}(\Theta)$

接下来：对 bias 和 variance 的进一步解释，以及确定问题后应采取怎样的措施。

10.5 正则化和偏差/方差

正则化的线性回归，$\lambda$ 不同会得到不同的结果。太大会造成 bias，太小会造成 variance。

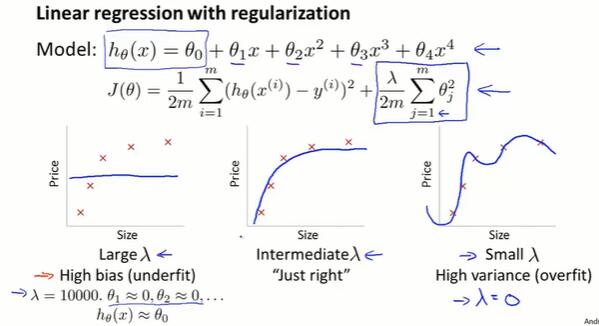
我们的模型：

训练模型的过程中，添加正则项，得到 $\Theta$ 。
评估模型的过程中，只计算偏差，不进行优化。不用添加正则项。

自动选择 $\lambda$：

选取一系列想要尝试的取值，对于每个 $\lambda$ 分别让 $J(\Theta)$ 取到最小值，获得 $\Theta$
在交叉验证集上评估它们。选择让 $J_{cv}(\Theta^{(i)})$ 取到最小值的 $\lambda$ 。
在测试集上测试这个模型的表现。

正则化的 bias/variance：

$J_{train}$：$\lambda$ 小，过拟合，训练集误差小；$\lambda$ 大，欠拟合，训练集误差大。
$J_{cv}$：$\lambda$ 小，过拟合，交叉验证集误差大（模型扩展性差）；$\lambda$ 大，欠拟合，交叉验证集误差大。

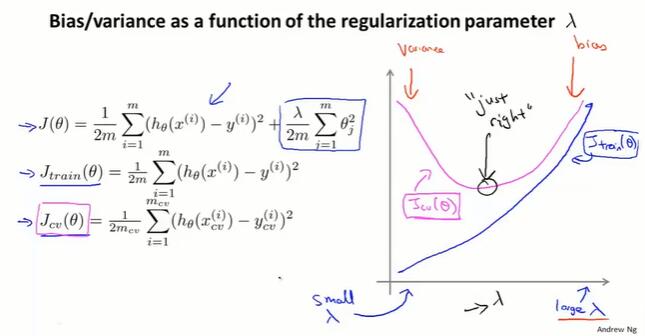
取多个 $\lambda$ 值，绘制交叉验证集误差 $J_{cv}(\Theta)$ 的曲线。

在真实的数据集中，得到的曲线可能更乱，有很多的噪声。有时可以看出一个趋势，通过观察整个交叉验证误差曲线，手动或自动得出能使交叉验证误差最小的 “just right” 的 $\lambda$ 取值。

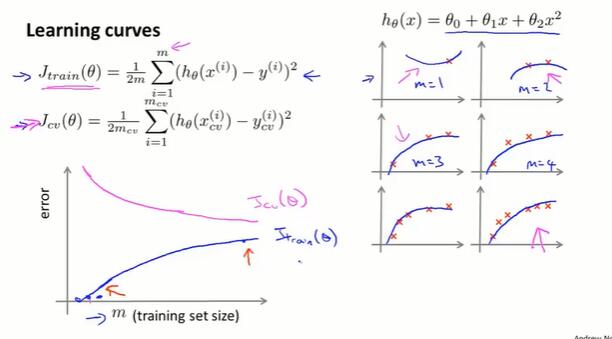
10.6 诊断方法：学习曲线（learning curves）

控制使用的训练样本数量，绘制小数据集的训练集误差、交叉验证集误差。

$J_{train}$：当训练集很小，拟合起来比较容易。当训练集增大，误差就会增加。
$J_{cv}$：当训练集很小，模型泛化程度不会很好。使用大的训练集，模型会有更好的泛化表现。

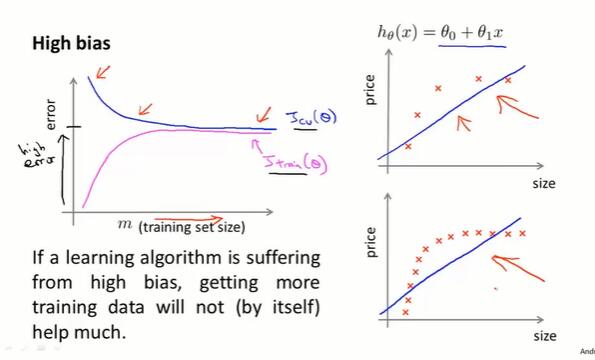
high bias 的学习曲线：

m 很小，拟合程度好（$J_{train}$小），泛化能力差（$J_{cv}$大）。
m 变大，$J_{cv}$ 和 $J_{train}$ 逐渐接近。当欠拟合时，训练集和交叉验证集上的表现都比较高，数值上相似。
结论：如果模型处在 high bias 的情形，选用更多的训练集数据对于改善算法的表现无益。

high variance 的学习曲线：

m 很小，拟合程度好（$J_{train}$小），泛化能力差（$J_{cv}$大）。
m 变大，拟合越来越难，但拟合程度也不错。泛化能力依然差。$J_{cv}$ 和 $J_{train}$ 逐渐接近。当欠拟合时，训练集和交叉验证集上的表现都比较高，数值上相似。
结论：如果模型处在 high variance 的情形，选用更多的训练集数据，延长这两条曲线，$J_{cv}$ 和 $J_{train}$ 会逐渐接近。这对改善算法的表现是有好处的。

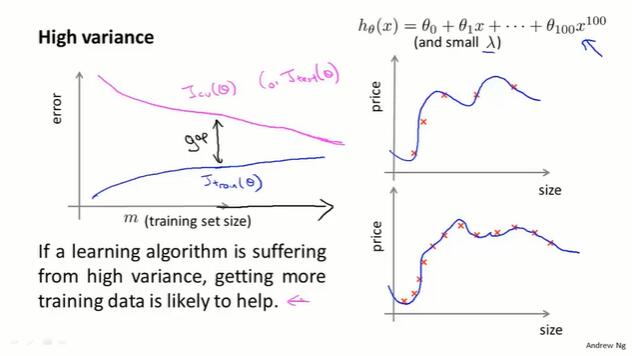
10.7 决定下一步做什么

回到10.1提出的改进方法：

改进方法	适用场合
更多训练样本	high variance
更少特征	high variance
更多特征	high bias
更多多项式特征	high bias
增加 $\lambda$	high variance
减小 $\lambda$	high bias

跟神经网络的结合

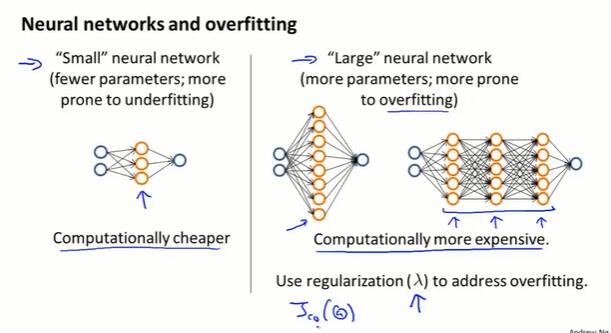
第十一章机器学习系统设计(Machine Learning System Design)

11.1 确定优先执行的事情

以垃圾邮件分类器为例：

监督学习，x = 邮件的特征，来表示一组词是否在邮件中出现。

事实上，有时会随机决定去采用上面四种方法的其中一种。

11.2 误差分析（error analysis）

在改进机器学习算法时，通常有很多不同的思想。通过误差分析，可以更系统地在众多方法中做出选择。

当在面对一个机器学习问题时，最好花很少的时间，先通过一个简单的算法，快速实现出来，而不是设计一个很复杂的系统。然后用交叉验证集来测试数据，画出学习曲线，进行检验误差，来确定模型是否存在高偏差或者高方差的问题，或其他问题。然后再决定是否要用更多的数据或者特征等。

可以把这种思想想成：在编程时避免出现过早优化的问题，我们应当用实际的证据来指导我们的决策，来决定把时间花在哪里，而不是仅凭直觉。

误差分析

误差分析：可以人工检查算法出错的地方，查看被分错了的邮件有什么共同的特征和规律。这个过程可以启发我们怎样设计新特征，或告诉我们现有系统的优点和缺点。

量化指标

如果算法能够返回一个数值指标，来估计算法执行的效果，将会很有帮助。

是否使用词干提取（stemming）？使用了会造成一些问题，不使用会忽略一些情况。

这时就可以使用交叉验证集上的错误率作为数值指标，来决定是否使用词干提取。

在此基础上，要不要区分大小写？也可以通过这个单一量化指标来轻松决定。

注意：不要再测试集上做误差分析。要在交叉验证集上做误差分析。

注意：最先实现的算法，简单粗暴为主，快是第一指标，再烂都没问题。

11.3 类偏斜的误差度量（error metrics for skewed classes）

上节提到了误差分析和设定误差度量值的重要性，那就是设定某个实数来评估学习算法并衡量它的表现。但仅用准确率accuracy来评价模型，在一种条件下是不可靠的，这个问题就是偏斜类的问题。

正样本的数量与负样本的数量相比，非常非常少，这种情况就叫偏斜类（skewed classes）。

精确度从99.2%提升到99.5%，不能说分类模型的质量提升了，因为有时模型恒定输出0，如果样本中y=0的比率比模型的预测准确率高，也能带来数值上的提升。

对于偏斜类，需要有不同的误差度量值：

查准率和查全率

precision：查准率、精确率。在预测为1的样本中，有多少是预测正确的？（没错诊）
recall：查全率、召回率。在真实为1的样本中，有多少是预测出来的？（没漏诊）

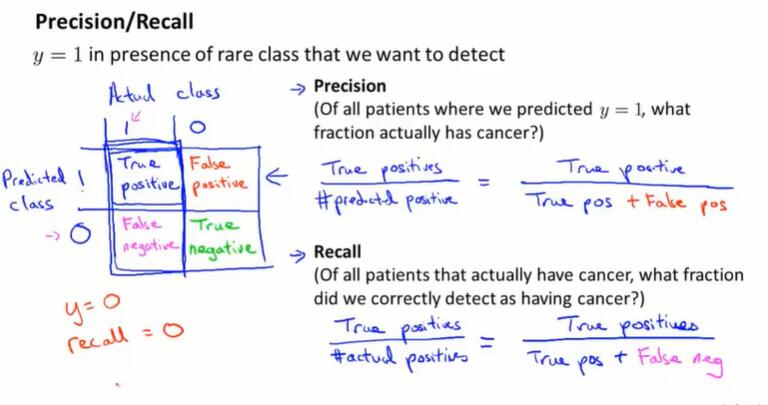
11.4 查准率和查全率之间的权衡（trading off precision and recall）

给没有病的人通知得病是不好的。为了提高precision，也就是降低误诊率，可以把逻辑回归的阈值设置得高一些。

这会导致：higher precision（有更高的把我才预测得病），lower recall（容易漏诊）
没有给得病的人通知也是不好的。为了提高recall，也就是降低漏诊率，可以把逻辑回归的阈值设置得低一些。

这会导致：higher recall（有病的人容易被预测到），lower precision（没病的人也容易被预测到）。

问题来了：有没有办法自动选取阈值？more generally，如果我们有不同的算法，如何比较不同的查准率和查全率？

在10.2，我们提出设置单个数值指标来评估模型的好坏。但现在我们有两个可以判断的数字 precision 和 recall。如何得到单个数值？

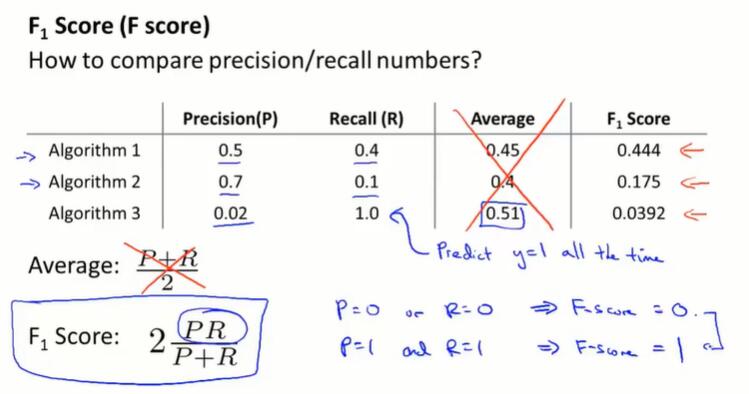
平均值是不行的。比如图中 Algorithm 3，恒输出y=1，显然不是一个好模型。

F₁ 值（调和平均值）共同考虑了两个值，并且给小的值更高的权重。

11.5 机器学习的数据

实验证明：给算法更多的数据，模型的性能往往会变好。

如何判断 feature x 是否包含了充足的信息，能够从中预测出 y？

判别方式：找一个人类专家，他能根据现有条件给出预测吗？

一个说英语的人，可以根据现有上下文填出 “two”；但一个房地产专家不能仅根据房屋面积预测房价。

如果 feature x 确实包含了充足的的信息用来预测 y ，大量的训练数据就是有帮助的。

使用一个有很多参数的学习算法（也被直接称为 low bias algorithm），在训练集上会得到不错的拟合效果，也就是 $J_{train}$ 比较小。

然后，用一个很大的训练集进行训练，模型就难以过拟合（low variance），在测试集上表现跟训练集上差不多，也就是 $J_{train}≈J_{test}$。

也就是：$J_{test}$ 比较小。

以上，我们证明了：做一个关键的假设如果特征值有足够的信息量，并有一类很好的学习算法保证low bias，那么——如果由大量的训练数据集，这能保证得到 low variance 的模型。

第十二章支持向量机(Support Vector Machines）

在监督学习中，很多监督学习算法的性能都很相似，所以经常要考虑的不是选择哪种算法，而是：构建算法时所使用的数据量。这体现了应用算法时的技巧，比如所涉及的用于学习算法的特征的选择，以及正则化参数的选择，等等。

还有一个更加强大的算法，有广泛的应用：支持向量机（support vector machine）。与逻辑回归、神经网络相比，SVM在学习复杂的非线性方程时，能提供一种更为清晰和更强大的方式。

12.1 优化目标（optimization objective）

从逻辑回归的损失函数定义SVM的损失函数

直观上：以直代曲。

跟逻辑回归的代价函数中的取对数部分相似，当 y=1，$cost_1(z)$ 让 z 越大越好；当 y=0，$cost_0(z)$ 让 z 越小越好。

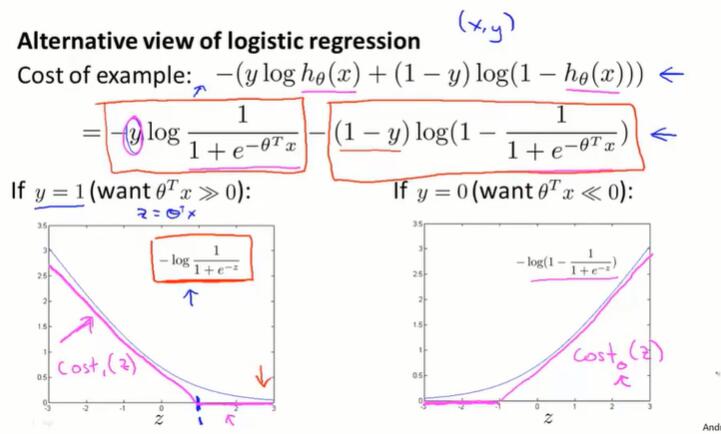
表达式上：

把取对数项换成 $cost_1(z)$ 和 $cost_0(z)$
去掉 $\frac{1}{m}$ （约定习惯。优化的结果不会变，依然是最佳值）
逻辑回归的损失函数形式上是 $A+\lambda B$，用 $\lambda$ 来权衡损失 $A$ 和正则化 $B$ 的相对权重（来决定我们是更关心第一项还是第二项的优化）。而在SVM里，使用 $CA+B$ 的形式，对 $C$ 赋值来权衡 $A$ 、$B$ 的相对权重。可以理解为$C = \frac{1}{\lambda}$。

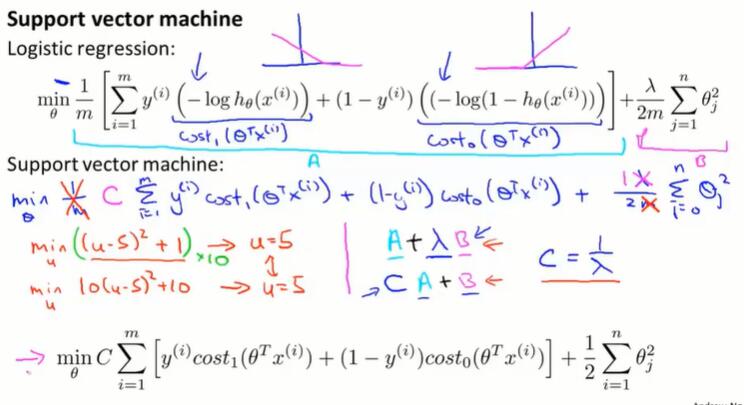
12.2 大边界的直观理解（large margin intuition）

有时候称 SVM 为大间距分类器（large margin classifier）。

从损失函数图像理解：

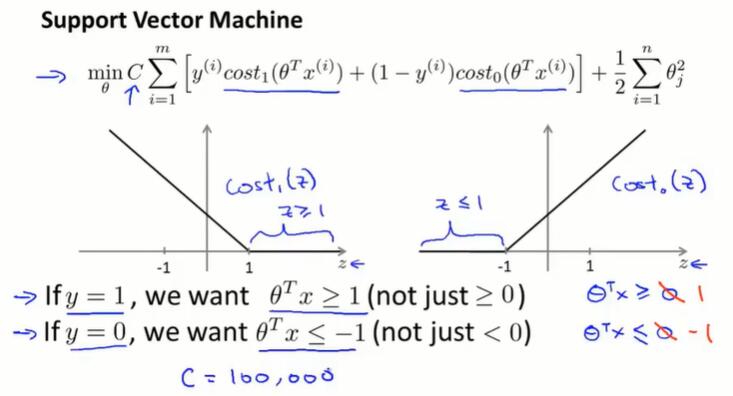
从损失函数表达式理解：

当 $C$ 取一个很大的值，在优化过程中我们希望让第一项为0。

逻辑回归：当$y=1$，我们希望 $z≥0$；当$y=0$，我们希望 $z<0$。

SVM：当$y=1$，我们希望 $z≥1$；当$y=0$，我们希望 $z≤-1$。

SVM的决策边界：SVM会尽量把正样本和负样本以最大的间距分开。

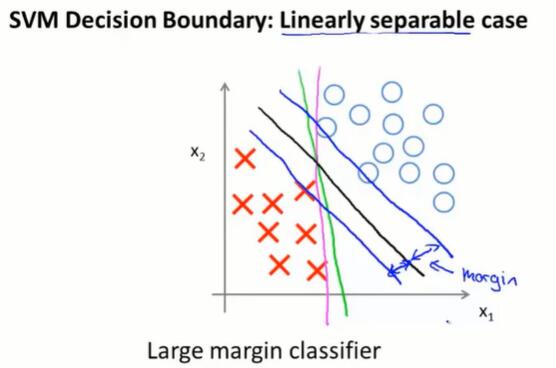
一个问题：只因为一个负样本分布比较偏，预测边界就从黑线转变为紫线，是不合理的。但如果把 SVM 的 $C$ 设置得非常大，因此会做这样的转变。

如果 $C$ 不是很大，或者模型本身不是线性可分的，那就不会有这样的问题。预测边界是黑线，SVM表现不错。

12.3 大边界分类器背后的数学原理*

SVM的优化问题和大间距分类器之间的联系

回顾向量内积：

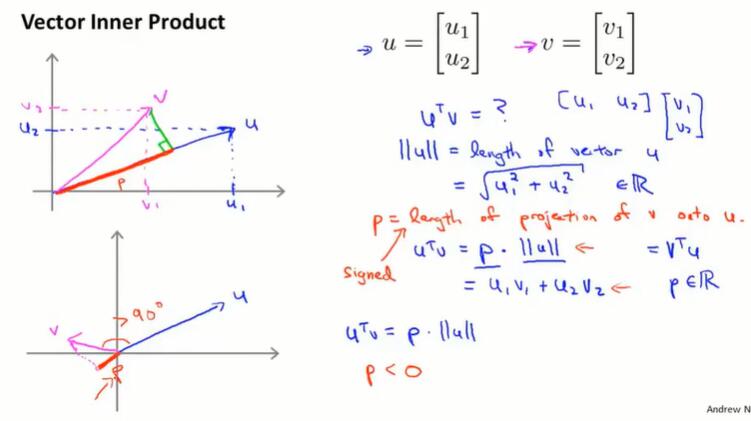
$u^T v = p·||u|| = u_1v_1+u_2v_2，$p 是 $v$ 投影到 $u$ 上的长度。

SVM 决策边界：

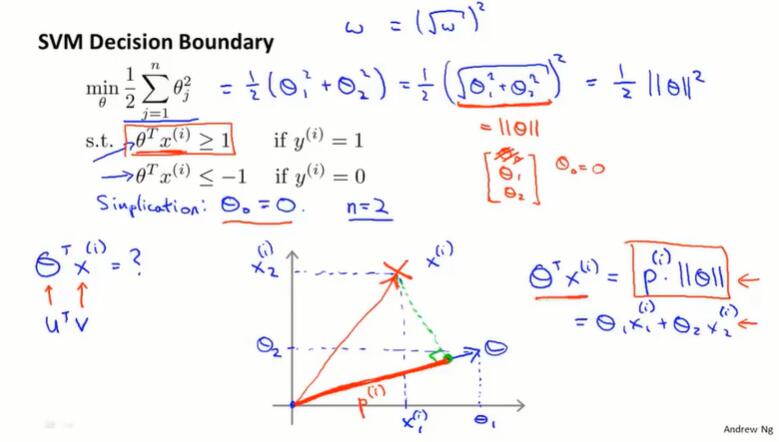
SVM 损失函数第二项，优化时，做的其实是最小化参数向量 $\theta$ 的范数（长度）的平方。

$\theta^Tx^{(i)}=p^{(i)}·||\theta||=\theta_1x_1^{(i)}+\theta_2x_2^{(i)}$

上式告诉我们：两个条件 $\theta^Tx^{(i)} ≥1$、$\theta^Tx^{(i)} ≤1$ 可以换种方式表述，即 $ p^{(i)}·||\theta||$ 的大小。

改写后：

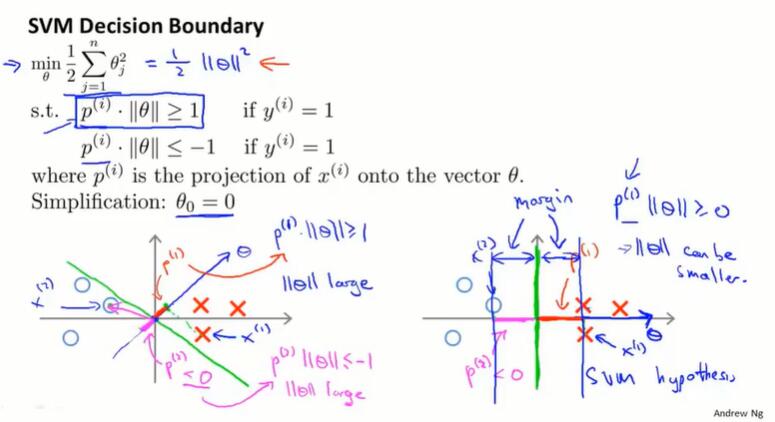
假设 $\theta_0=0$ ，决策边界通过原点，决策边界一定与 $\theta$ 向量垂直。以 $\theta_1x_1+\theta_2x_2≥1$ 为例，$x_2 = -\frac{\theta1}{\theta2} x_1 + a$ ，跟 $\theta$ （斜率 $\frac{\theta_2}{\theta_1}$）是垂直的。
左图绿色的决策边界，会导致 $x$ 到 $\theta$ 的投影长度较小。我们又要求 $ p^{(i)}·||\theta||≥1$ ，因此 $\theta$ 的范数要比较大。
右边绿色的决策边界，会导致 $x$ 到 $\theta$ 的投影长度比较大。要求 $ p^{(i)}·||\theta||≥1$ ，可以把 $\theta$ 优化到很小。
在SVM中，要求对于大多数数据点， $\theta^Tx ≥1$，也就是说，正样本、负样本的数据点投影到 $\theta$ 的值足够大，就是使决策边界周围保持大间距，让 $p^{(i)}$ 尽量大。

12.4 核函数Ⅰ

改造 SVM，来构造复杂的非线性分类器

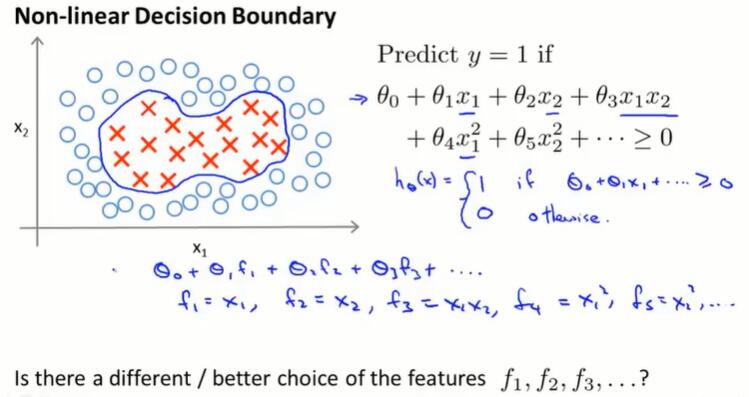
非线性决策边界的拟合，需要很多的高阶多项式项，给计算带来麻烦。

是否有更好的特征选择方式？

每个特征是 x 与 l 的相似度 $f_i = similarity(x, l^{(i)}) = exp(-\frac{||x-l^{(i)}||^2}{2\sigma^2})$

这个相似度函数 similarity(x, l) 就是核函数，在这里是高斯核函数。

相似度函数（核函数）的作用：

这些特征 f 的作用就是衡量 x 到 l 的相似度。越相近，f 越接近 1；越不相近，f 越接近 0.

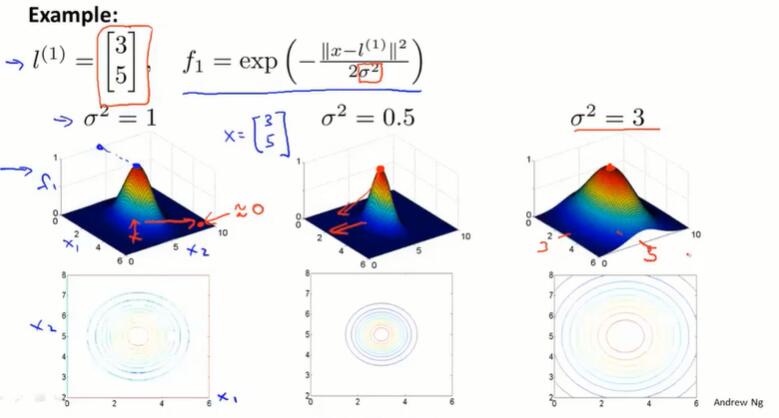
$\sigma$ 越大，从把 x 从 l 点移走时，特征变量的值 f 下降得越慢。

从特征到预测函数

通过前面的核函数，可以从 x 得到特征 f 了，并且越接近 f_i 对应的 l_i ，f_i 的输出越接近1。

通过学习到每个特征对应的 $\theta$，就可以进行预测，拟合复杂的非线性边界了。

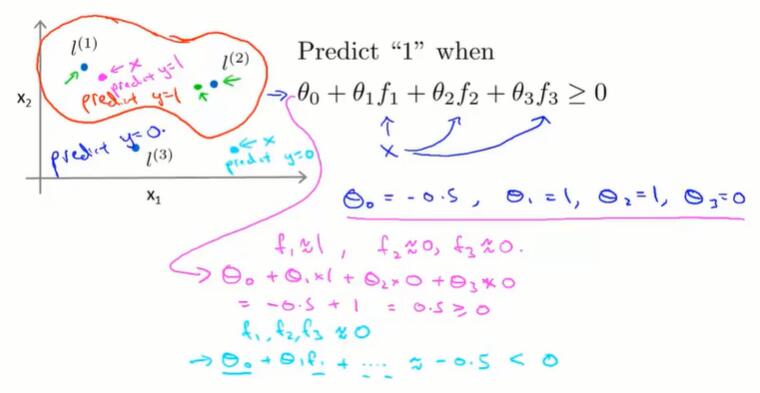
以图中的 $\theta$ 取值为例，接近 $l_1,l_2$ 的点，预测的结果为 1；远离 $l_1,l_2$ 的点，预测的结果为 0.

现在已经学习了核函数，以及如何在 SVM 使用核函数，来定义新的特征变量了。

还有一些问题：如何选择标记点 $l$？其他的核函数（相似度函数）是什么样的？

12.5 核函数Ⅱ

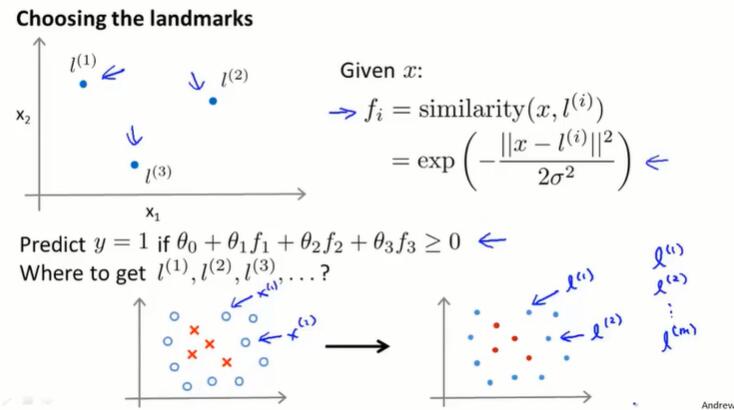
如何选择 landmarks？

一种方法：把数据集的 m 个样本都选择为 landmarks，即 $l^{(i)}=x^{(i)}$。

如上图对于每个输入 x，把它转换成一个 m 维的特征向量 $f^{(i)}$.

SVM 的训练

注意：

在优化时设置 $\theta^Tf≥1$ ，在预测时用 $\theta^Tf≥0$
忽略掉 $\theta_0$后，最后一项正则化也可以用 $\theta^T\theta$ 来计算。
由于所有样本都设置为关键点，有 m = n，正则化项求和边界没变。
在逻辑回归等算法也可以采用核函数的思想，来设置关键点，但在计算上没有 SVM 特有的优化方法。
这个函数的优化不建议自己实现，调包即可。

SVM 的参数，偏差和方差

C（理解为 $\frac{1}{\lambda}$)
- C 大：拟合项权重大，正则化项权重小，容易过拟合。low bias, high variance。
- C 小：拟合项权重小，正则化项权重大，容易欠拟合。high bias, low variance。
$\sigma^2$
- $\sigma^2$ 大：$f$ 平缓，模型随x的改变，变化不明显，容易欠拟合。high bias, low variance。
- $\sigma^2$ 小：$f $ 陡峭，变化明显，容易过拟合。low bias, high variance。

12.6 使用支持向量机

不需要自己写 SVM 优化软件，但需要手动：

选择参数 C
选择核函数
- 无核函数（也叫线性核函数）
  - predict “y = 1” if $\theta^Tx≥0$
  - 线性关系（$\theta_0+\theta_1x_1+…+\theta_nx_n≥0$)
  - 如果有大量的特征值和很少的训练数据集（n大，m小），就拟合一个线性的判定边界，而不去你和一个非常复杂的非线性函数，防止过拟合
- 高斯核函数
  - $f_i = exp(-\frac{||x-l^{(i)}||^2}{2\sigma^2})$，where $l^{(i)} = x^{(i)}$
  - 选择参数 $\sigma^2$
  - 如果特征值少，训练集数据多（n小，m大），用高斯核函数是一个好的选择

核函数的编写：

很多 SVM 优化函数需要核函数作为参数传入
核函数返回一个实数
在使用高斯核函数前需要做 feature scaling

核函数的选择：

核函数需要通过 mercer’s theorem 检查，确保能够正常优化
其他的核函数
- 多项式核函数（Polynomial kernal）
  - $k(x, l) = (x^Tl+constant)^{degree}$
  - 通常用在 x 和 l 都是严格的非负数时，以确保内积一定不是负数
- string kernel, chi-square kernal, histogram intersection kernel, …

多分类任务：

很多包都内置了多分类 SVM 功能
如果没有，使用 one-vs-all 思想（见6.7）：如果有 k 个类别，就训练 k 个 SVM ，用以将每个类别从其他的类别中区分开来。会得到 k 组 $\theta$，预测时取最大值的索引作为分类结果。

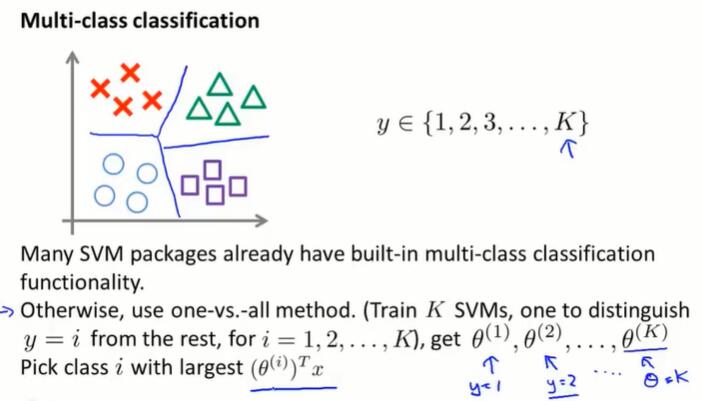
逻辑回归 vs SVMs：

n 是特征的个数（$x∈\R^{n+1}$），m 是训练集样本个数

n 比 m 大很多（如有10000个词特征，只有1000篇邮件来训练）：使用逻辑回归或无核函数（线性核函数）
n 很小，m 大小适中（n=1~1000，m=10~10000)：高斯核函数表现好
n 很小，m 很大（n=1~1000，m=~50000+）：高斯核函数会跑的很慢。如果训练样本特别多，尝试添加更多特征，然后使用逻辑回归或无核函数（线性核函数）

在所有的场合，设计良好神经网络都可以表现的很好。缺点是比起好的SVM包，神经网络训练得比较慢。在实际应用中，对于神经网络，局部最优是一个不大不小的问题；但SVM的优化是凸函数优化，在使用SVM时不需要担心这个问题。

第十三章聚类(Clustering）

13.1 无监督学习简介（unsupervised learning introduction）

监督学习：我们有一系列标签，然后用假设函数去拟合它。

无监督学习：我们的数据并不带有任何的标签。

聚类算法的应用：

市场分割
社交网络分析
组指计算机集群
天文数据分析

13.2 K均值算法（K-means algorithm）

输入：

K：聚类的个数
训练数据集 ${x^{(1)},x^{(2)},…,x^{(m)}}$
- $x^{(i)}∈\R^n$，无监督学习的x是 n 维向量而不是 n+1 维

随机初始化 K 个聚类中心 $\mu_1, \mu_2,…,\mu_k ∈ \R^K$

循环：

样本划分：对于每个训练集的样本，把值设置为最接近的聚类中心的值
移动聚类中心：对于每个聚类中心，把所有值相同的训练样本求平均，得到新的聚类中心
- 如果有聚类中心没有一个训练样本，常见的做法是移除这个聚类中心

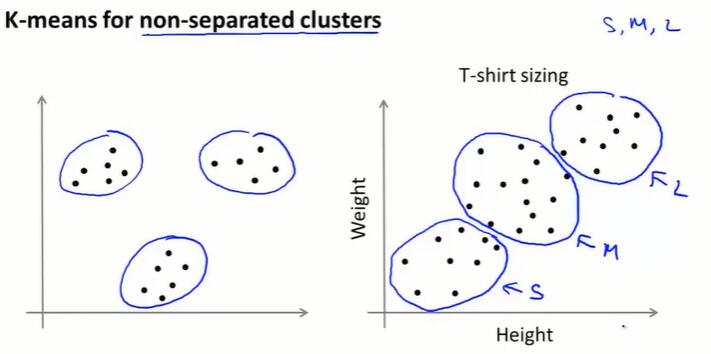
即使数据没有明确分为几簇，K-means算法还是能将数据分为几个簇。

13.3 优化目标（optimization objective）

了解K-means的优化函数，能帮助我们：

对学习算法进行调试，确保算法正确运行
帮助算法找到更好的簇，并避免局部最优解（下节讲）

K-means算法的代价函数：训练样本到聚类中心的接近程度

K-means算法的优化目标：调整聚类中心 $\mu$ 、样本划分 $c$ ，让代价函数取到最小值

每次迭代：

先样本划分：改变 $c^{(i)}$，不改变 $\mu_k$，优化代价函数 $J$ 关于变量 $c$
后移动聚类中心：改变 $\mu_k$，优化代价函数 $J$ 关于变量 $\mu$

13.4 随机初始化（random initialization）

如何初始化 K-means、如何使 K-means 避开局部最优

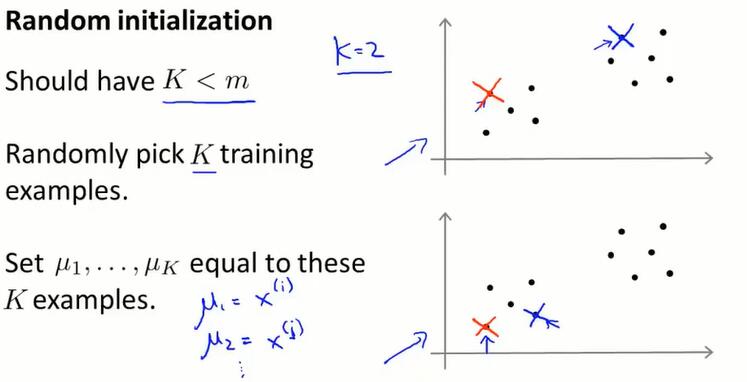
从 $x^{(i)}$ 里随机找 K 个聚类中心，这就是随机初始化。随机初始化状态不同，K-means最后可能会得到不同的结果。特别地，K-means 可能会落在局部最优。

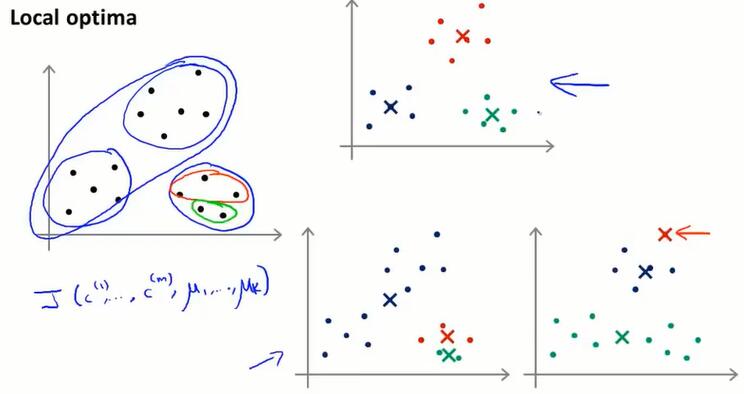
我们可以以不同的初始值初始化 K-means 很多次，并执行算法很多次，以此来保证我们最终能得到一个尽可能好的局部或全局最优值。

具体做法如下：

多次随机初始化 K-means 算法，分别求代价函数，在其中找最小的 $J$ .当 K 不是特别大（不超过10），一般都能得到比较好的结果。

13.5 选择聚类个数K（choosing the number of clusters）

这个问题没有什么好的答案，也没有能自动处理的方法。用来决定聚类数量最常用的方法仍然是：人工，人为观察可视化的图，或者观察聚类算法的输出。

无监督学习没有给出标签，因此并不总是有一个明确的答案。也是因为这个原因，用算法自动选择聚类个数是困难的。

肘部法则（elbow method）：改变 K 的值，计算损失函数 $J$，选择“elbow”的点作为 K 的个数。（每次计算 $J$ 都要随机取个100次的初始聚类中心，这个计算消耗是不小的。）有时这个肘部也不太好找。总之：这是个值得尝试的方法，但不能指望它解决问题。

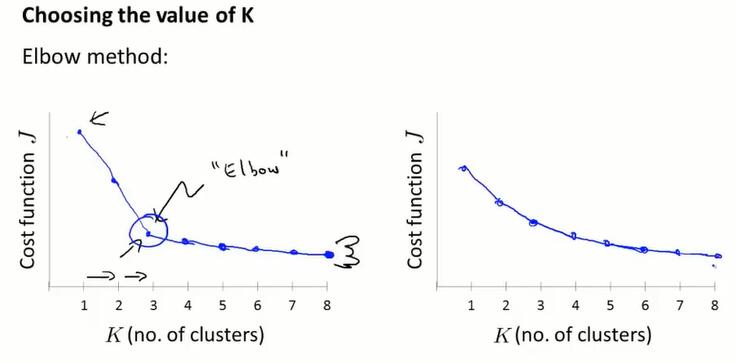
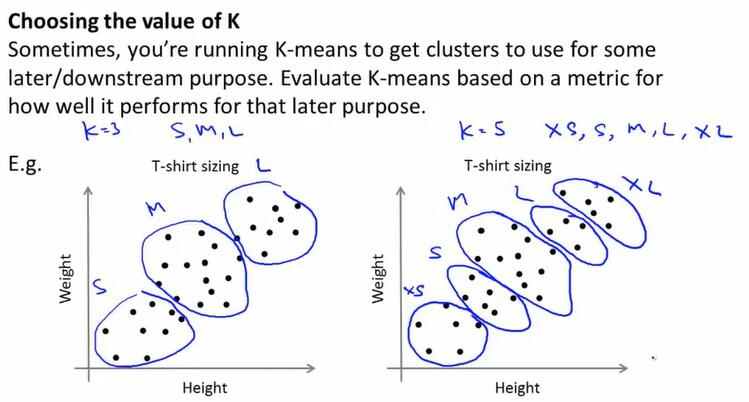
从下游找K值：聚类往往是要解决问题的，比如T恤分为 S、M、L 三个聚类，从类似的下游环节寻找聚类个数。

第十四章降维(Dimensionality Reduction）

14.1 动机一：数据压缩（data compression）

数据压缩不仅能让我们节省存储空间，还能对学习算法进行加速。

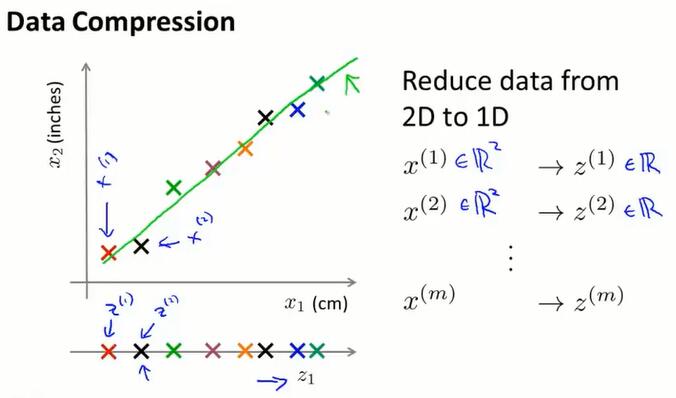
我们需要一个二维向量 $x^{(i)}∈\R^2$ 来表示一个样本的两个特征值。有时候这两个特征是冗余的，特征值可能是线性的。

如果能通过投影绿线上的样本来近似原始的数据集，那只需要一个实数 $z^{(i)}∈\R $ 就能指定点在直线上的位置。

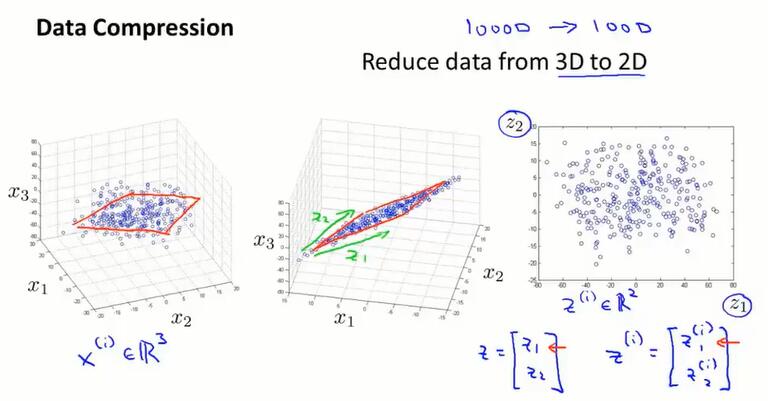
从 3D 到 2D 的降维也是一样的：三维中的数据大概都分布在一个平面内，所以我们通过把所有数据都投影到一个二维平面上来进行降维。

这样，使用二维向量 $z^{(i)}∈\R^2$ 可以表示三维坐标。

14.2 动机二：数据可视化（data visualization）

数据可视化可以帮助我们理解数据。

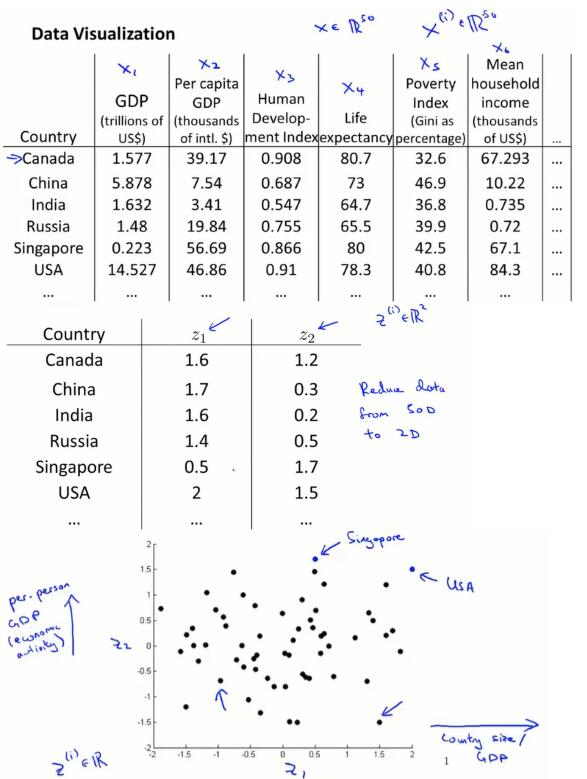
以图中50维的国家数据为例，如果能只用两个数字，来概述50个数字，就可以把这些国家在二维平面上表示出来。

当观察降维算法的输出时，z 通常不是所期望的具有物理意义的特征，我们常常要弄清楚这些特征大致意味着什么。

比如图中，横轴表示国家的“体量”，纵轴表示国家的“人均”。

14.3 主成分分析问题（principal component analysis problem formulation）

主成分分析算法（PCA）是很常用、很流行的降维算法。

PCA

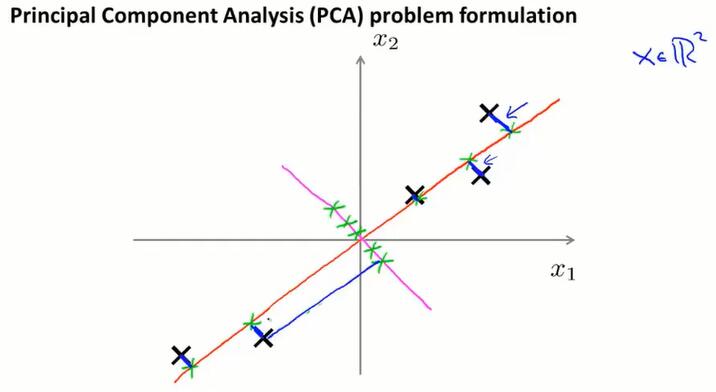
PCA算法会找一个低维平面（图中红线），然后将数据投影在上面，使数据到低维平面的距离最小（图中蓝色小线段）。

更正式地说：当从n维降到k维，需要找出一个方向（找出k个向量 $u^{(i)}∈\R^n$，定义这个k维空间）。PCA能够找出最小化投影距离的方式，来对数据进行投影。

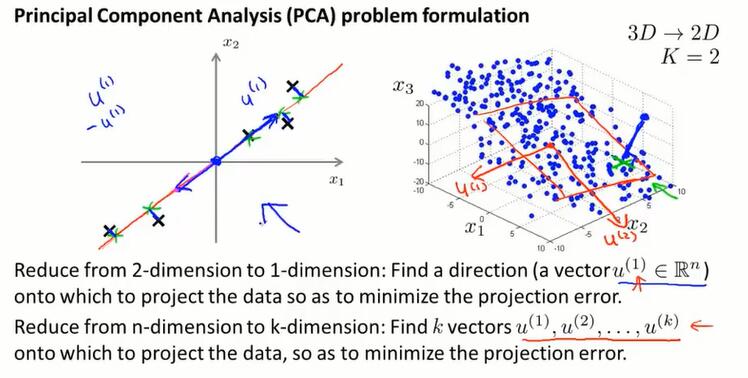
PCA和线性回归

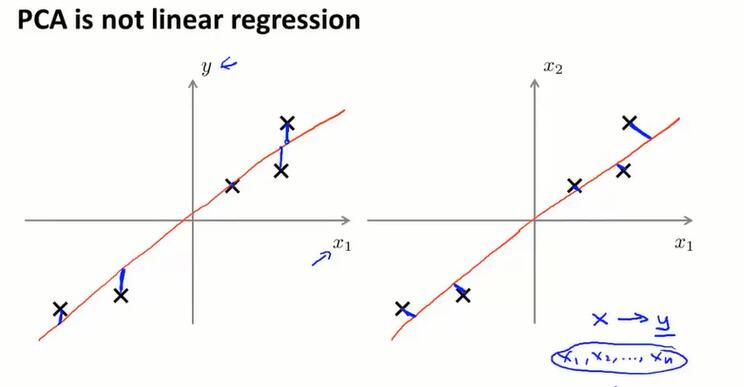
PCA和lr看上去相似，但确实是两种完全不同的算法。

线性回归：最小化预测值和实际值的距离。用x预测y。

PCA：最小化投影距离（正交距离）。都是特征x，没有需要特殊对待的y。

14.4 主成分分析算法（principal component analysis algorithm）

首先要进行 feature scaling、mean normalization 等数据预处理工作。

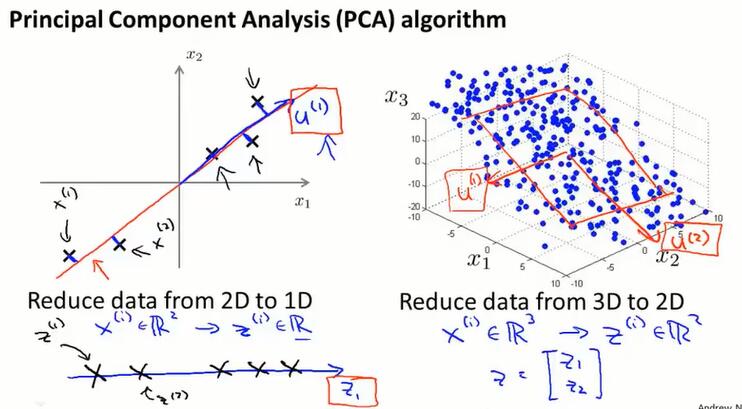
PCA 算法需要做的两件事：求出定义了降维空间的向量 $u$；求出样本在降维空间的投影 $z$。

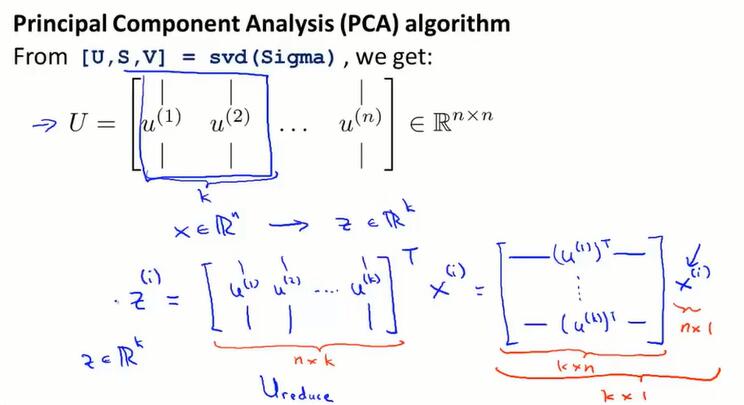
PCA算法：

先计算协方差矩阵 $\Sigma$，再计算 $\Sigma$ 的特征向量 $U$.

$U$ 是 (n, n) 维矩阵，它的前 $k$ 列就是要求的 k 维空间的方向向量 $u^{(1)}, u^{(2)}, …,u^{(k)}$ 。

把这些向量$u^{(1)}, u^{(2)}, …,u^{(k)}$ 构建成 $U_{reduce}$ 矩阵 (n, k)维，通过公式 $z = U_{reduce}^TX$ 可以求的 k 维空间的样本 $z$ 。

PCA算法总览：

本节没有给出数学上详细的证明，来证明 $u$、$z$ 就是让误差平方最小的投影方法。

14.5 选择主成分的数量（choosing the number of principal components）

本节将讨论如何选择降维后的维度 k。

投影误差可以理解为放弃的特征值，总方差理解为全部的特征值。

选择k的通用原则是：选择使不等式成立的最小k。

意思是：保留更多的方差。

找k的算法的实现如下，可以使用 svd(Sigma) 返回的S来简化计算。

只需要运行svd函数一次，就可以进行这些运算。

$\frac{\sum^k_{i=1}S_{ii}}{\sum^m_{i=1}S_{ii}}≥0.99$这个式子也可以用来表示 k 值选的好不好。如果我们把特征从1000维降到100维，可以使用这个不等式来衡量降维对于特征保留的性能。

14.6 降维重建（reconstruction from compressed representation）

怎样从 $z∈\R$ 得到 $x∈\R^2$？

求$z$的公式是 $z=U_{reduce}^Tx$，$U$不是方阵，没有逆矩阵，不能直接算。 $x_{approx}=U_{reduce}z$。由于PCA要求投影不能跟数据点离得太远，所以 $x_{approx}$ 差不多就是 $x$。

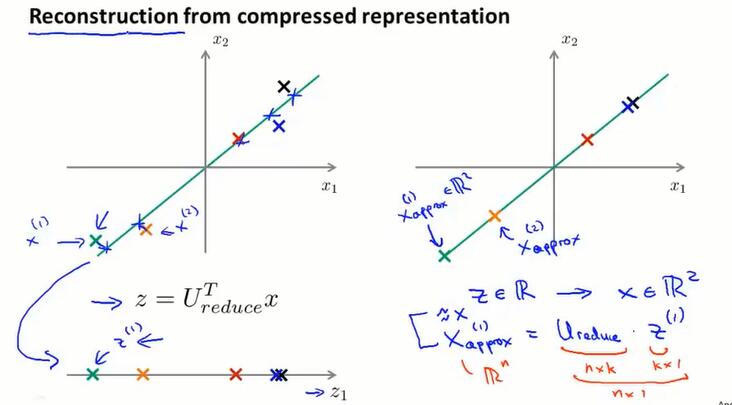
14.7 主成分分析法的应用建议（advice for applying PCA）

PCA是如何提高算法执行效率的？

应用PCA的注意事项

PCA建立了从 $x$ 到 $z$ 的映射关系，这个映射关系只能通过在训练集上运行PCA得到。

这个映射所做的就是计算一系列参数，比如进行特征缩放和均值归一化，还计算了$U_{reduce}$，找到合适的k值等。我们应该只在训练集上拟合这些参数，而不知交叉验证集或测试集上。

在训练集上找到所有参数后，就可以把这个映射用在交叉验证集或测试集的其他样本中。

以图中为例，只在训练集的数据上运行PCA，从 $x$ 到 $z$ 建立映射，然后在 $z$ 和 $y$ 之间拟合机器学习算法（低维数据提高了算法的运行效率），当要做预测时，就把交叉验证集和测试集中的数据也映射为 $z$（映射用的矩阵 $U_{reduce}$也只能从训练集得来），然后通过机器学习算法得出预测结果。

PCA的应用场景

PCA的主要应用场景：

不同的应用场景要选择不同的k值。

PCA的错误应用场景：

PCA能给数据降维，减少特征数量。所以有人会认为PCA可以用来防止过拟合。

如果这样做了，可能效果也会很好，但这不是解决过拟合的好方法。更好的解决过拟合的方法是：使用正则化。

原因：PCA不使用标签y，仅使用输入的x，去寻找接近的低维数据。PCA扔掉一些信息来减少数据的维度，并且不关心y的值。PCA更有可能丢失一些有价值的信息。

PCA的另一个误用：

经常在一个项目开始时，一些人会写一个项目计划，其中包括PCA在内的四步。

在写下这样的计划之前，要先问这个问题：如何直接去做而不使用PCA会怎样？

只有在使用原始数据 $x^{(i)}$ 达不到预期效果时（运行太慢，需要提高效率；内存不够、硬盘不够，需要压缩数据），才考虑使用PCA和 $z^{(i)}$。

第十五章异常检测(Anomaly Detection）

这是机器学习算法的一个常见应用，它的有趣之处在于：虽然主要用在非监督学习问题，但从某个角度看，跟有监督学习问题是非常相似的。

15.1 问题的动机（problem motivation）

从给定无标签的数据集，对数据建模 $p(x)$，对于新数据，如果 $p(x{test})＜\epsilon$ ，就将它标记为 anomaly。

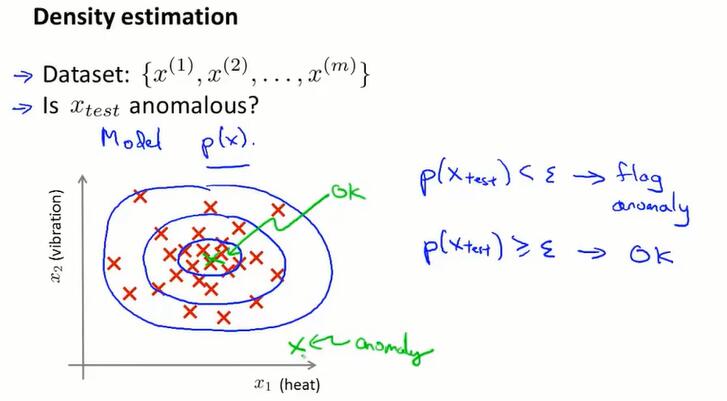
应用举例：

网站欺骗检测。$x^{(i)}$ 是用户 $i$ 的行为，包含如登录次数、点击速度等信息；对数据建模得到 $p(x)$；对 $p(x{test})＜\epsilon$ 的 anomaly 的用户进行身份验证，或开启防御动作。
工业生产领域。如找到异常的机器。$x^{(i)}$ 是计算机 $i$ 的状态，包含如内存占用、CPU占用等信息；对数据建模得到 $p(x)$；对 $p(x{test})＜\epsilon$ 的 anomaly 的计算机进行监视，防止异常出现。

15.2 高斯分布（gaussian distribution）

高斯分布

高斯分布也叫正态分布 $x\sim N(\mu,\sigma^2)$，$\mu$ 是中心值， $\sigma$ 是标准差（$\sigma^2$是方差）。

公式：

$$ p(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2}) $$

$\sigma$ 越小，图像越窄；无论参数如何变，图像的积分一定是1 。

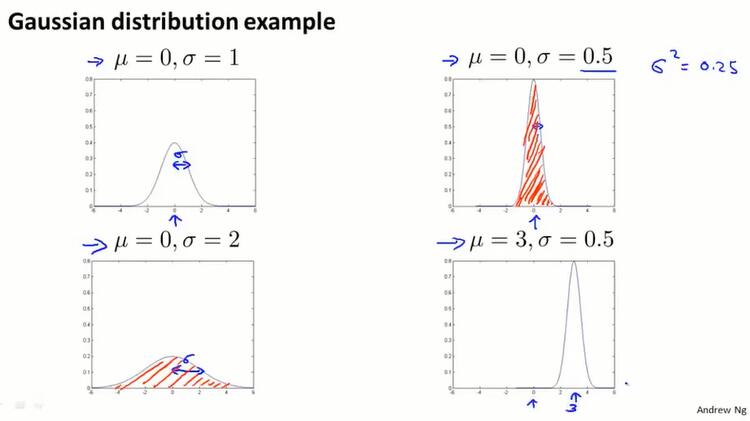
参数估计

假设 $x^{(i)}$ 符合高斯分布，但不知道 $\mu$ 和 $\sigma$ 的值。

$\mu=\frac{1}{m}\sum^m_{i=1}x^{(i)}$，均值
$\sigma^2=\frac{1}{m}\sum^m_{i=1}(x^{(i)}-\mu)^2$，方差，也是对 $\mu$ 和 $\sigma^2$ 的极大似然估计

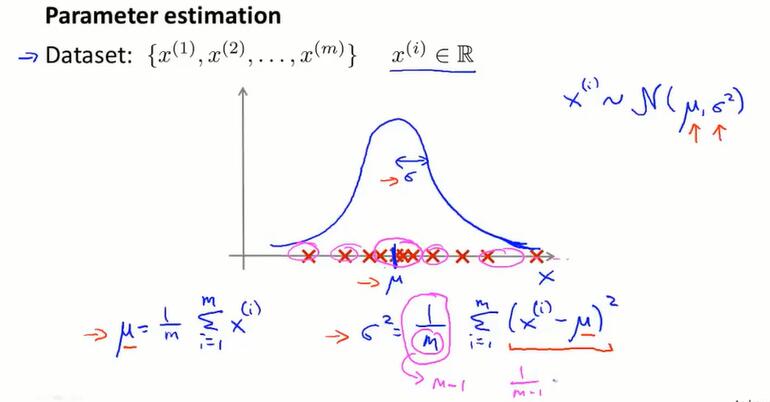
15.3 异常检测算法（algorithm）

每个特征都随机取值，都服从一个高斯分布，等同于一个 $x_1$ 到 $x_n$ 的独立同分布。

$$ p(x) = \prod^n_{j=1}p(x_j;\mu_j,\sigma_j^2) $$

异常检测算法总览：

先选一些符合数据分布特征的例子；根据这个数据集训练高斯分布的参数；进行估计。

独立同分布相乘的直观理解：

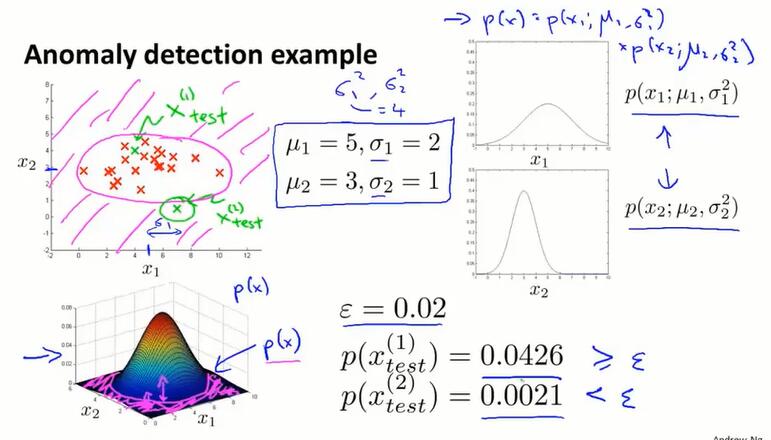
粉色是 anomaly 区域。

15.4 开发和评价一个异常检测系统（developing and evaluating an anomaly detection system）

如何开发一个异常检测的应用来解决实际问题；如何评估一个异常检测算法。

之前讲到了用实数评估的好处。如果在异常检测算法也有这样的实数是比较好的。

训练集是non-anomalous的，在交叉验证集、测试集中，假设是有标签的并且含有anomaly数据（y=1代表anomaly）。图中展示了两种可行的划分方法（第二种把同样的数据同时用在交叉验证集和测试集是不推荐的）：

异常检测算法的评估：

首先在训练集上拟合函数 $p(x)$。

因为数据很倾斜（y=1的情况很少），使用这些指标来评估：真/假阳/阴性，查准率和查全率，F1分。

可以在交叉验证集上尝试多个 $\epsilon$ 的值，并选择让F1分最高的那个，或在其他方面有良好表现的那个。

交叉验证集的作用就是可以尝试不同的特征组合、参数值，来选择最佳的配置。

得到了配置，就在测试集上进行最终的评估。

15.5 异常检测与监督学习对比（anomaly detection vs. supervised learning）

在上一节，我们使用了带标签的数据集来评估异常检测算法，这与监督学习有什么异同？为什么不用逻辑回归或神经网络来预测 y=0 或 y=1？分别在什么情况下使用两者？

异常检测中，有很少的正样本和很多的负样本，当在估计 $p(x)$ 的值，拟合所有高斯参数的过程中，我们只需要负样本就可以了。所以如果有大量的负样本，仍然可以拟合出很好的 $p(x)$。

异常检测中，有很多种类的正样本难以观测（比如有不同的原因导致发动机宕机）。如果只有很少的正样本，很难充分学习到正样本的种类是什么；并且，未出现的异常也很难被预测到。所以，放弃对正样本建模，只对负样本建模。

监督学习中，在正常范围内有足够的正、负样本。监督学习算法查看大量正负样本，并且能够进行种类的区分。

应用对比上，区别还是在数据集中正样本的数量大小。如果给异常检测的正样本收集了足够多的数据，就可以用监督学习算法来预测。

15.6 选择特征（choosing what features to use）

选择用什么特征来实现异常检测算法。

如何调整特征分布

特征选择的原则：最好让数据更接近高斯分布。

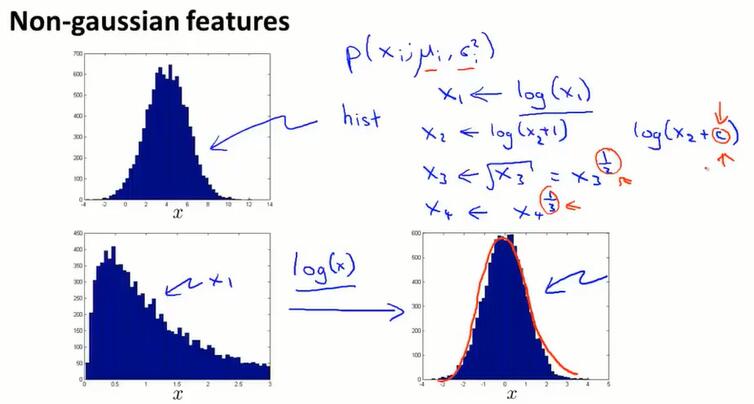
如何选择特征

跟监督学习类似，先训练一个算法，在交叉验证集上人工查看预测出错的部分，并考虑能否找到一些其他的特征来表达这些判断出错的样本的特性。

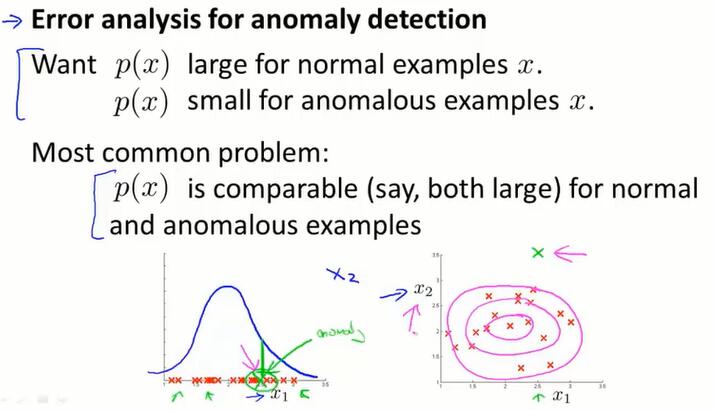
如图，只用 $x_1$ 作为特征，发现了异常点。再给数据建模添加特征 $x_2$ 后，就发现异常产生的原因了。

举例：

CPU负载和网络负载在有些时候是线性的，也有些时候CPU负载高而网络负载低（如本机死循环）。添加了特征 $x_5$ 或 $x_6$ ，就能捕捉这种情况了。

15.7 多元高斯分布*（multivariate gaussian distribution）

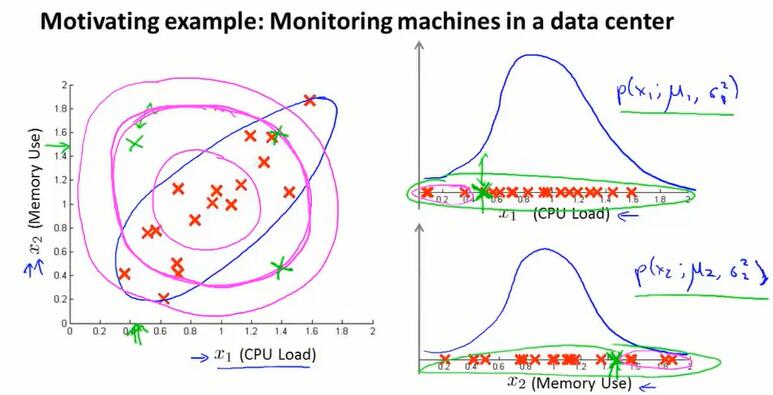
绿点离样本分布有距离，应该被判断为anomaly，但异常检测算法计算 $p(x^{(i)})$ ，看上去检测不出来这个异常。异常检测算法学习到的是粉色范围，而不是蓝色范围。

为了解决这个问题，使用多元高斯分布。

$\Sigma\in \R^{n\times n}$ 是协方差矩阵，参见 14.4PCA算法的协方差矩阵。PCA第一步是均质归一化，就不用减去平均值了。

使用这个矩阵一次算出所有特征的概率 $p(x)$。公式：

$$ p(x;\mu,\Sigma)=\frac{1}{(2\pi)^\frac{n}{2}|\Sigma|^\frac{1}{2}}exp(-\frac{1}{2}(x-\mu)^T\epsilon^{-1}(x-\mu)) $$

增大 $\Sigma$ 的某个对角线值（增大某个特征分布的方差），对应x下降得更缓慢；减小 $\Sigma$ 的某个对角线值（减小某个特征分布的方差），对应x下降得更缓慢。

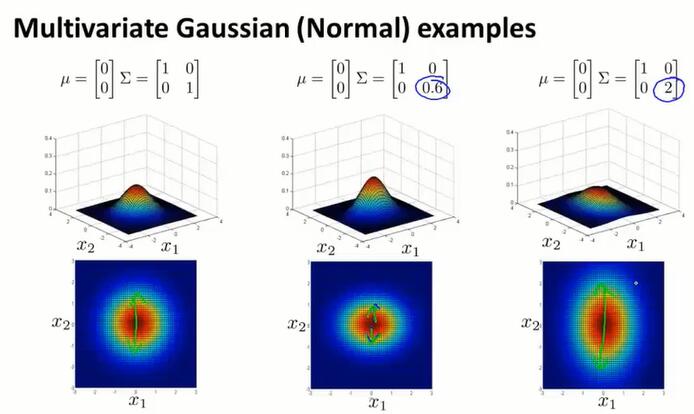
通过多元高斯分布，可以描述斜着的样本分布.越接近1，越跟横轴长度相似：

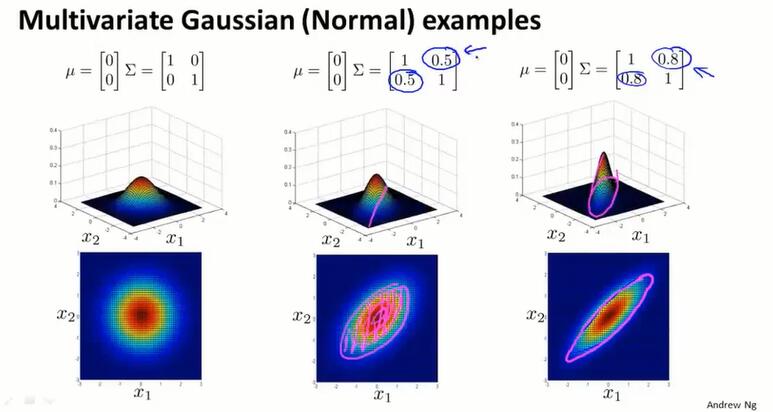
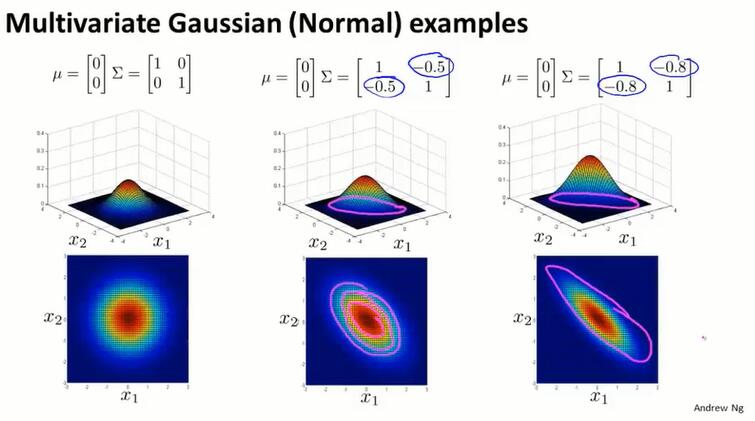
也可以改变 $\mu$ 的值，来改变山顶的位置：

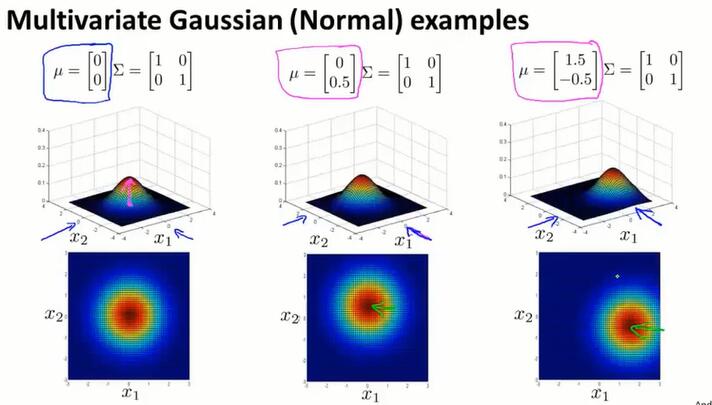
15.8 使用多元高斯分布进行异常检测*（anomaly detection using the multivariate gaussian distribution）

步骤和公式

从数据集得到多元高斯分布的参数 $\mu$ 和 $\Sigma$：

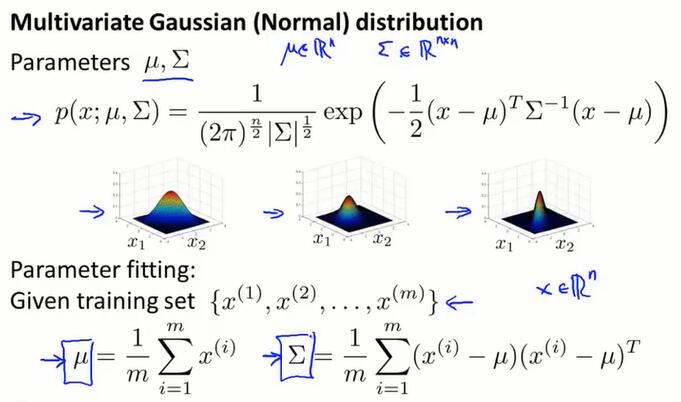
计算 $p(x)$，得到椭圆形的分布估计：

多元高斯分布模型和原始模型的区别

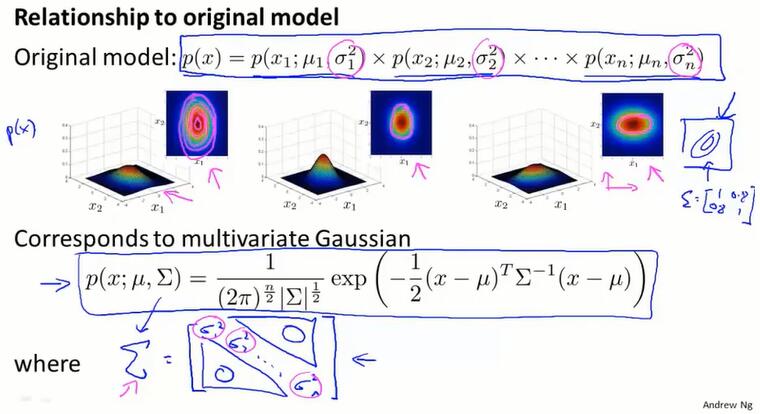
原始模型不包含特征间的关系。特征的分布如果是独立的，概率分布函数就可以拆开相乘。这种拆开乘的原始模型，实际上就是某种特殊情况下（特征间不相关，即$\Sigma$ 的非主对角线都是0）的多元高斯分布。此时分布图象关于x，y轴是“正”的。

多元高斯模型的 $\Sigma$ 非主对角线不为0，也就是特征间有相关，不能写成拆开相乘的形式。这时的分布图象是“斜”的。

如何在两个模型之间做选择：

原始模型：

手动组合异常，来捕捉异常样本（如CPU负荷低网络负荷高，需要创建新的特征，见15.6）
计算简单，可以计算巨大的特征数量
参数不多训练容易，既使数据样本很少，也能拟合出好模型

多于高斯模型：

可以自动捕捉特征间的关系
有 $\Sigma^T$ 操作，计算要求高
必须 $m>n$ ，即样本数量多于特征数量，来保证 $\Sigma$ 可逆；$\Sigma\in\R^{n\times n}$ 的参数很多，实践上最好 $m>>n$

多元高斯分布 $\Sigma$ 不可逆的原因：

不满足 $m>n$
有线性相关的特征，造成冗余

第十六章推荐系统(Recommender Systems）

推荐系统是机器学习的一个重要应用。推荐系统的性能提升在学界仅占很小的讨论份额，但在企业里是很重要的。

特征学习是机器学习中很重要的思想。对于某些问题，一些算法可以自动学习一系列的特征，在有些环境下我们可以编写一个算法来学习使用哪些特征，推荐系统就是一个例子。通过推荐系统，可以了解一些特征学习的思想。

16.1 问题规划（problem formulation）

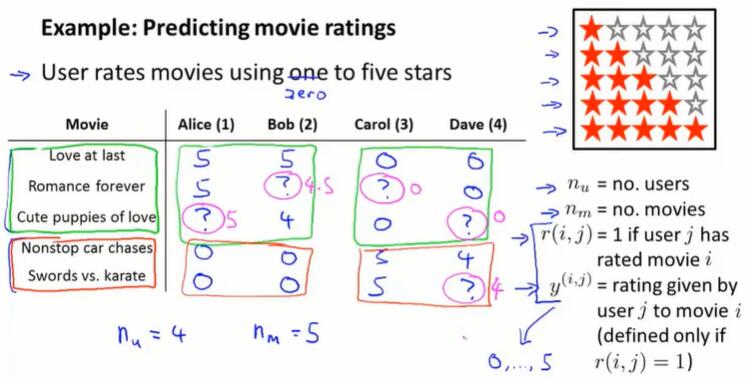
$n_u$：user 的数量
$n_m$：movie 的数量
$r(i, j)$：user i 是否给 movie j 打过分
$y(i, j)$：user i 给 movie j 打了几分（$r(i, j)=1$ 时有定义）

推荐系统就是开发一个算法，能够为我们填补这些缺失值。然后在用户还没看过的电影中，预测用户喜欢的电影，并推荐给该用户。

16.2 基于内容的推荐算法（content-based recommendations）

基于内容的意思是：我们假设已有电影内容的特征向量 $x^{(i)}$（描述电影类型）。

基于内容的推荐算法就相当于线性回归：

每一部电影有一个题材向量 $x$，$x_1$ 评价电影的爱情要素，$x_2$ 评价电影的动作要素，$x_3$ 是偏置项1。

每一个用户 $j$ 有一个评分向量 $\theta^{(j)}\in \R^{(n+1)}$。根据该用户的过往评分拟合出这个向量。

对于新电影，用 $(\theta^{(j)} )^T x^{(i)}$ 预测用户 $j$ 对电影 $i$ 的评分。

更普遍的线性回归过程：为了简化表达式，将评分过的电影数量 $m^{(j)}$ 去掉。

线性回归的优化目标：所求是每一个用户的喜好 $\theta^{(j)}$。

梯度下降：

对于许多电影来说，我们并没有内容的特征向量 $x^{(i)}$，下节将介绍不是基于内容的推荐系统算法。

16.3 协同过滤（collaborative filtering）

基于内容的推荐系统是我们已经拥有了内容向量（如一个电影拥有多少爱情元素，拥有多少动作元素），但实际上我们很难得到这个内容向量。并且，我们通常需要除了爱情、动作之外的其他特征，如何得到这些新特征？

协同过滤算法有一个很有趣的特性：特征学习。这种算法能够自行学习所要使用的特征。

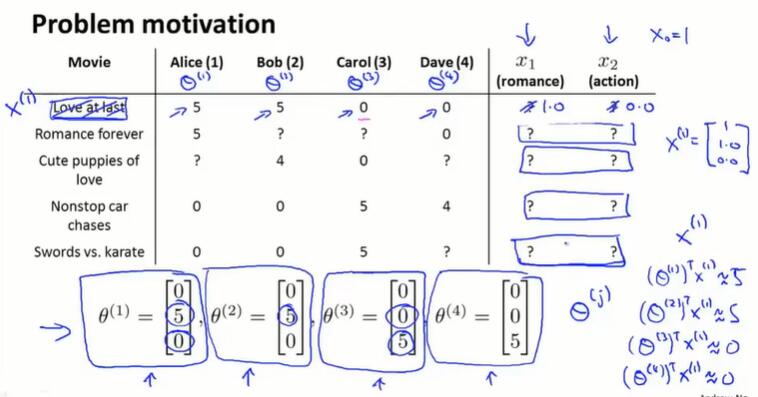
我们不知道内容向量，但每个用户告诉了我们对每种电影的喜爱程度 $\theta^{(j)}$。对于电影 $x^{(1)}$，我们知道 $\theta^{(1)},\theta^{(2)}$ 喜欢并且 $\theta^{(3)},\theta^{(4)}$ 不喜欢，那么可以推断 $x^{(1)}$ 是爱情片而不是动作片，并可以根据 $(\theta^{(j)})^T x^{(1)}\approx r(1, j)$ 计算出 $x^{(1)}$ 的具体值。

所求是每一部电影的内容向量 $x^{(i)}$：

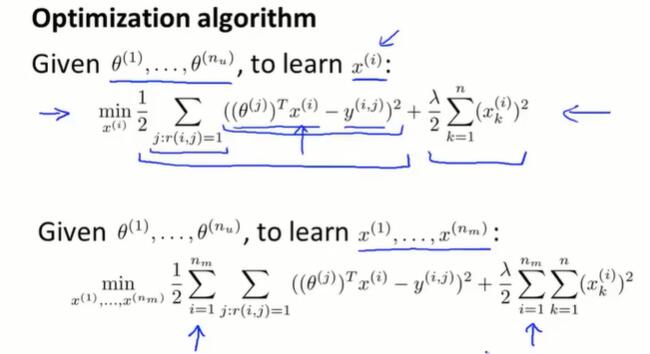
这节和上节的算法可以形成协同过滤的迭代过程：

从一个初始用户喜爱向量 $\theta$ 开始，可以不断进行梯度优化，得到更准确的用户喜好 $\theta$、电影类型 $x$，并且得到好的推荐系统。

16.4 协同过滤算法（collaborative filtering algorithm）

在前两节，我们学习了：

给出电影的特征，可以用来学习用户的参数 $\theta$
给出用户的参数，可以用来学习电影的特征 $x$

有一种更高效的算法，我们不需要不停的交替计算 $x$ 和 $\theta$，而是能同时计算 $x$ 和 $\theta$。

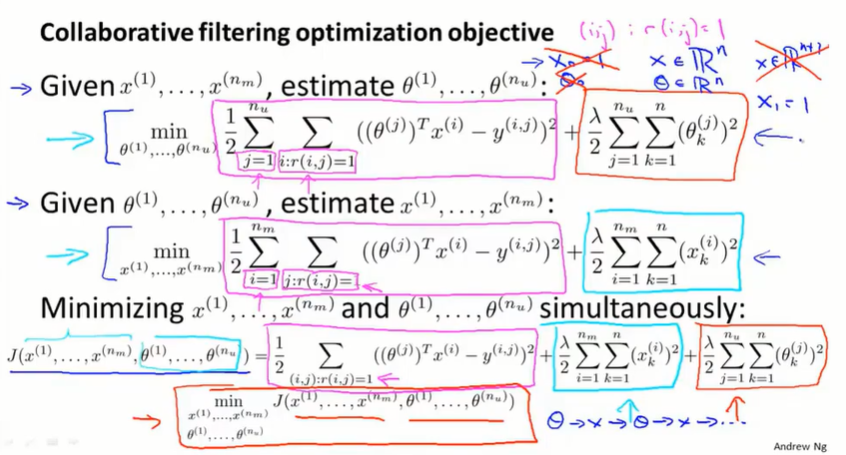
取消了偏置项，即 $x_0,\theta_0$。因为算法要学习很多的特征，如果需要一个特征永远为1，可以选择靠自己去获得这个参数，比如把 $x_1$ 学习为1。让 $x$ 和 $\theta$ 自己学习线性关系，不需要人为加截距项。

协同过滤算法：

用小的随机数初始化，有点像神经网络的初始化
进行梯度下降，最小化 $J$
用 $\theta^Tx$ 进行预测

16.5 向量化：低秩矩阵分解（vectorization : low rank matrix factorization）

低秩矩阵分解就是协同过滤的向量化求解过程：

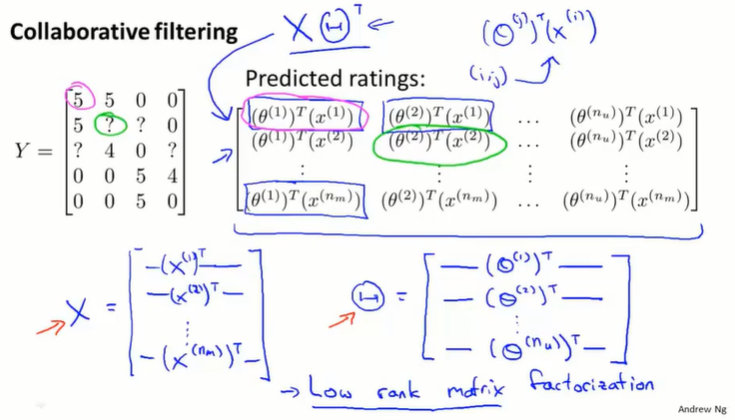
通过电影内容向量 $x$ 可以度量电影之间的相关性：

16.6 实现细节：均值归一化（implementational detail : mean normalization）

如果一个用户没有给任何的电影评分，那在梯度下降最小化 $J$ 的过程中，会学习到 $\theta^{(j)} = 0$。如果用 $\theta^Tx$ 做预测，会将所有的电影分数预测为0分，并且不会给用户做任何推荐。

均值归一化让我们解决这类问题。

给评分矩阵 $Y$ 减去评分均值 $\mu$，然后将新矩阵进行协同过滤，在预测阶段再把 $\mu$ 加回到预测的评分上。

对于没有评分的用户，会预测为平均分，推荐给他大家都觉得好的电影。

对于没有人评分的电影，不推荐给任何用户。

第十七章大规模机器学习(Large Scale Machine Learning）

处理大数据集的算法。

17.1 大型数据集的学习（learning with large datasets）

如果数据集 m=1亿，梯度下降的每一步都要对 m=1亿项求和，计算代价太大了。

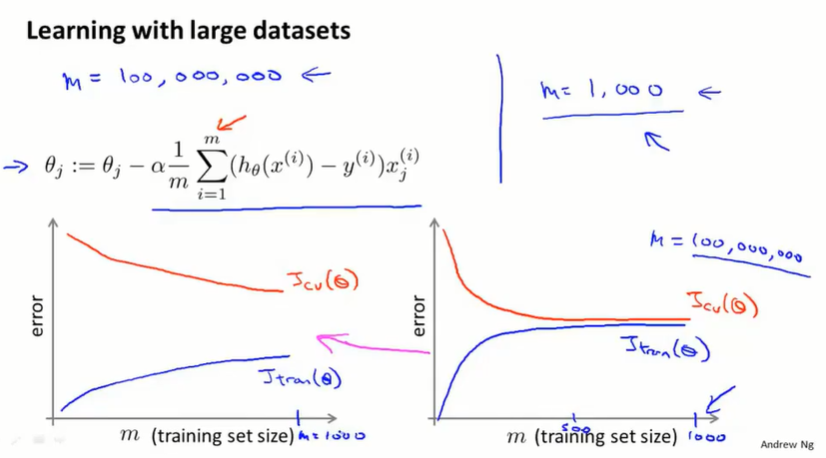
在高偏差的情况下，让数据集增大效果不好；在高方差的情况下，增大数据集一般是有效的。

详见 10.6学习曲线

17.2 随机梯度下降（stochastic gradient descent）

batch gradient descent：批量梯度下降，每次要同时考虑所有的训练样本。

如果数据集很大，对计算时间、内存容量都有很高的要求。

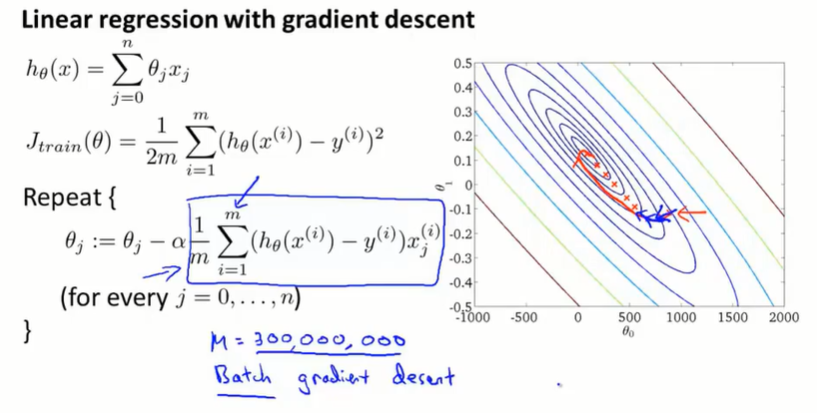
stochastic gradient descent：随机梯度下降，先打乱数据集，然后用单个数据样本进行梯度下降。内层循环遍历所有数据样本，外层循环控制遍历次数，一般取1~10。

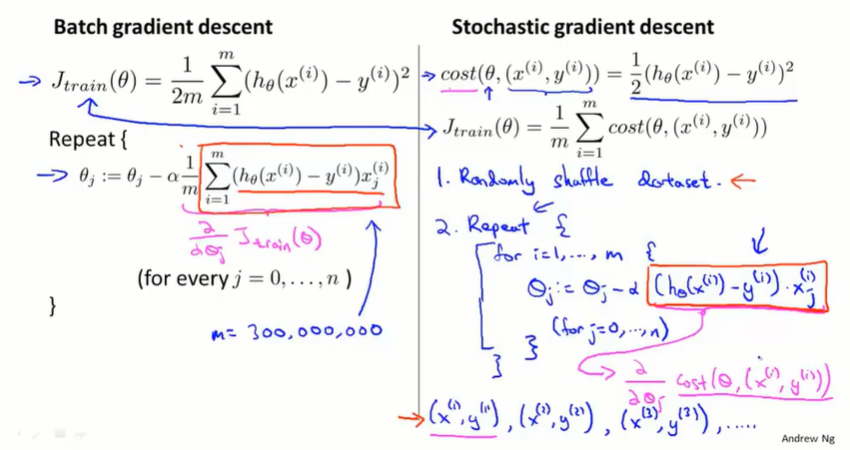
批量梯度下降每次迭代取平均的梯度，直接向最优点收敛（红线）；随机梯度下降每一次迭代都会更快，每次只需保证能拟合某一个训练样本就可以了，每一步不一定都向最优点收敛，但总体上也能到达最优点（粉线）。

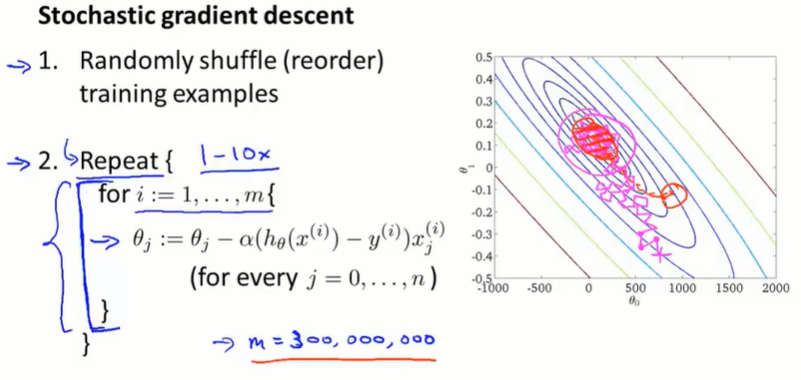
17.3 小批量梯度下降（mini-batch gradient descent）

批量梯度下降迭代慢、收敛快；随机梯度下降迭代快、收敛慢。小批量梯度下降是两者的折中方案。

一次取 b 个样本进行小批量梯度下降，b 一般取 2~100。

小批量梯度下降可能会比随机梯度下降算法更好，仅当：有一个好的向量化方法。在这种情况下，对一批 b 个样本的偏导求和能以更向量化的方式执行，这将使我们在 b 个样本中实现部分并行计算（同时计算 b 个）。

17.4 随机梯度下降收敛（stochastic gradient descent convergence）

在运行随机梯度下降算法时，如何确保调试过程已经完成，并且已经收敛到合适的位置呢？怎样调整随机梯度下降种学习速率 $\alpha$ 的值？

在批量梯度下降中，通过绘制 $J(\theta)$ 的图像来判断收敛。原因是批量梯度下降的每一次迭代，代价函数都是减小的。需要在算法运行过程中扫描一遍整个数据集来计算当前的 $J(\theta)$ ，所以数据集很大的时候也不好用。

随机梯度下降每次只考虑一个单独的样本，每次让算法前进一点，就不需要停下算法来计算 $J(\theta)$ 了。只需关注单个样本 $(x^{(i)},y^{(i)})$ ，在用该样本更新 $\theta$ 之前，计算 $cost(\theta, (x^{(i)},y^{(i)}))$ 。并且在一定量的数据样本的迭代后，打印 $cost$ 的平均值。

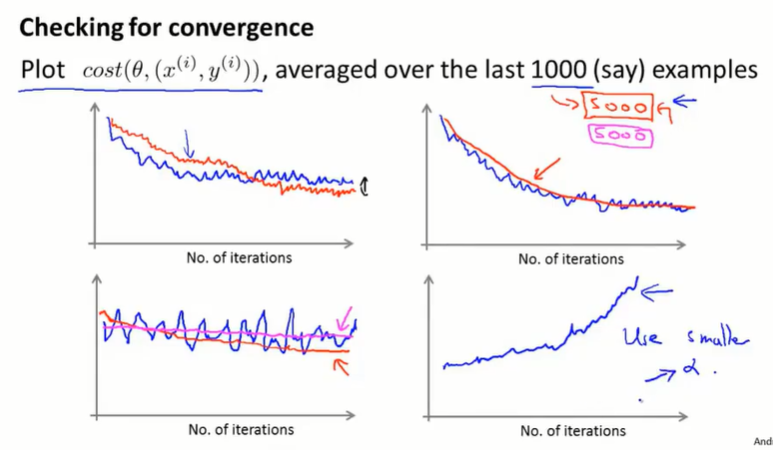
图左上：学习率大和小。学习率小的收敛结果可能更好。

图右上：计算 $cost$ 均值的数据量越大，曲线越平滑。缺点是求均值的数据量大，得到的反馈有延迟。

图左下：少的数据量求平均，看上去没有在学习收敛（蓝线）；但大的数据量求均值，可以看出函数实际上是在收敛的过程中的（红线）。如果大学习量求均值，函数也不收敛，就是算法出了问题（粉线）。

图右下：$cost$ 在增加，函数发散了。需要用更小的学习率 $\alpha$。

关于学习率：

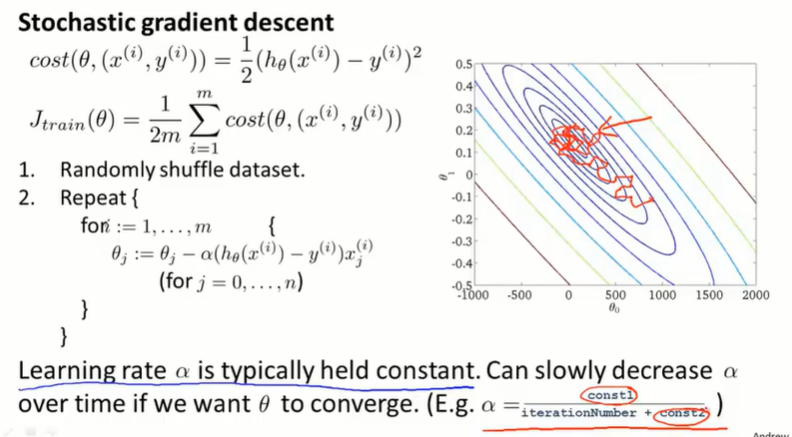
随机梯度下降的结果是在最小值附近震荡，如果想让随机梯度下降更好地收敛到全局最小值（震荡的幅度小），可以让学习率 $\alpha$ 随时间变化逐渐减小。但同时，也会带来新的确定参数的工作。

17.5 在线学习（online learning）

我们有连续一波数据或连续的数据流，想要用算法来学习。

跟随机梯度下降很相似，区别是：在线学习不使用固定的数据样本 $(x^{(i)},y^{(i)})$ ，而是根据目前的数据流 $(x, y)$ 来训练模型。这要求数据流比较多，这样就不用重复学习同样的样本了。

还有一个好处，就是这样可以适应用户喜好随着时代的变化。

另一个应用场景：预测点击率，并进行推送。

17.6 映射化简和数据并行（map-reduce and data parallelism）

前面的梯度下降算法都能在单个计算机上运行。但有时候可能数据太多了，不想把所有数据都在一台电脑上跑一遍。

map-reduce：

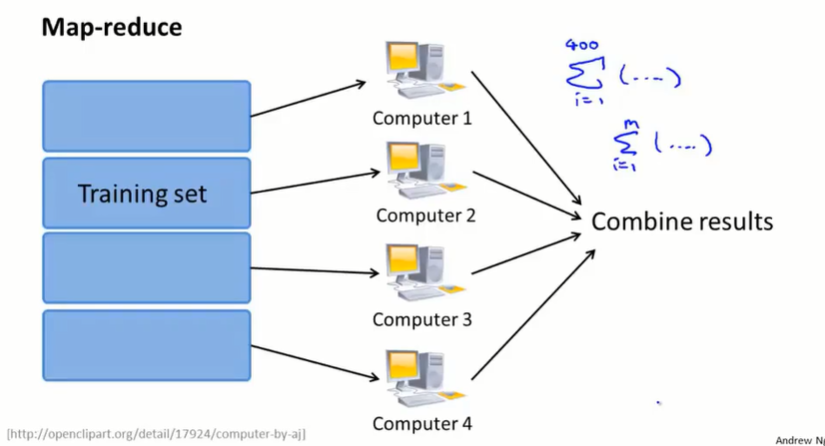
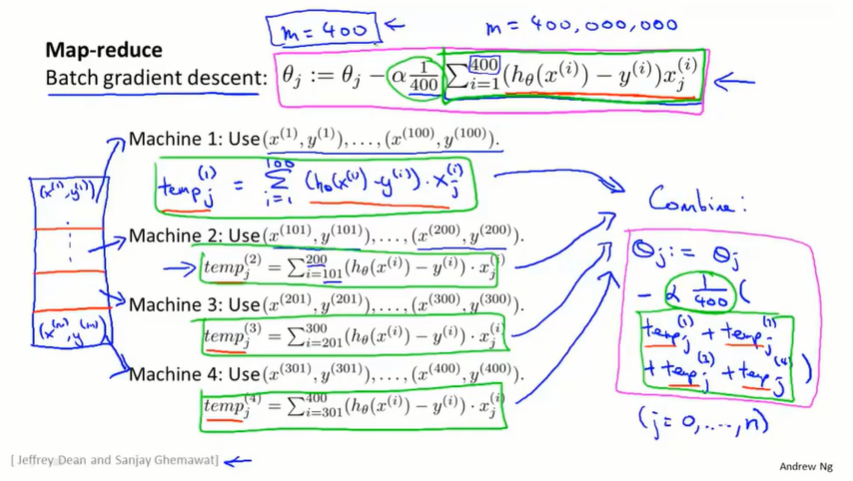
批量梯度下降：

在单个主机上计算 $\theta_j :=\theta_j-\alpha\frac{1}{400}\sum_{i=1}^{400}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$

map-reduce：

将数据集分成几部分，在不同的主机上计算 $temp_j^{(t)}=\sum_{}^{}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$
然后在整合服务器上计算 $\theta_j :=\theta_j-\alpha\frac{1}{400}\sum temp_j^{(t)}$。

实际上，很多学习算法都可以表示成对训练集函数的求和，而在大数据集上运行所消耗的运算量就在于需要对非常大的训练集进行求和。所以只要学习算法可以表示为对训练集的求和，或者学习算法的主要工作可以表示成对训练集的求和，那么就可以使用 map-reduce 将学习算法的适用范围扩大到非常大的数据集。

举例：如果使用高级优化函数来训练logistic算法，需要计算两个重要的量：一个是对于高级学习算法，需要提供一个过程来计算优化目标的代价函数 $J_{train}(\theta)$ ，第二个是计算偏导数 $\frac{\partial}{\partial \theta_j}J_{train}(\theta)$。将这两个求和过程分散给多个主机，然后把结果整合起来，就获得总的损失和总的偏导项，接着将这两个值交给高级优化算法。

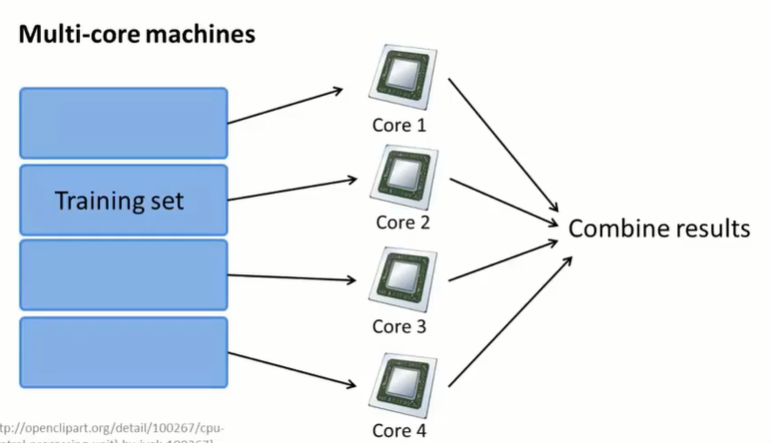
也有时候可以在单个电脑上进行 map-reduce。有的电脑又多个CPU，CPU又有多个核心。如果有一个很大的数据集，可以在单机上分给不同的核心来计算。

也有些线性代数库，可以自动进行多核运算。

第十八章应用实例：图片文字识别(Application example : Photo OCR）

一个复杂的机器学习系统是如何组织起来的。

机器学习pipeline的相关知识，以及如何分配资源。

机器学习中一些有用的想法和概念，如：如何将机器学习运用到计算机视觉问题中；人工数据合成的概念。

18.1 问题描述和流程（problem description and pipeline）

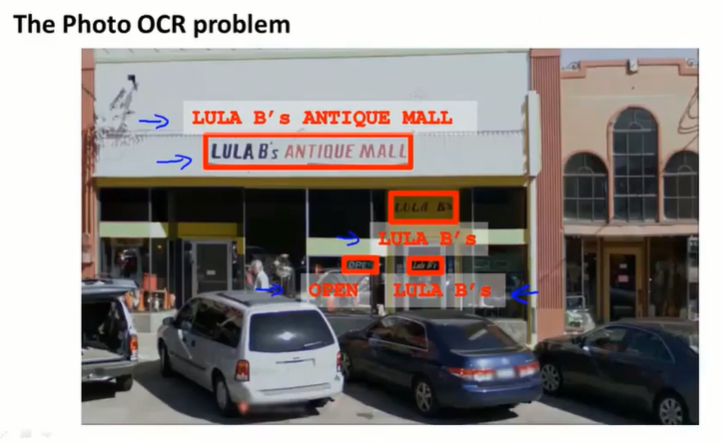
pipeline：

找出有文字的图像区域
进行字母分离
分类器识别字母

在机器学习实践中，很重要的一步就是设计机器学习的pipeline，如何将整个问题分为一系列不同的模块。

18.2 滑动窗口（sliding windows）

pipeline第一步：检测文字区域

行人检测任务：

训练阶段，矩形的长宽比例比较固定。可以构建监督学习模型，根据带有标签的数据集，学习预测是否含有行人。

预测阶段，使用滑动窗口：建立不同尺寸的滑动窗口，按照一定的步长，取一系列图像，判断是否含有行人。

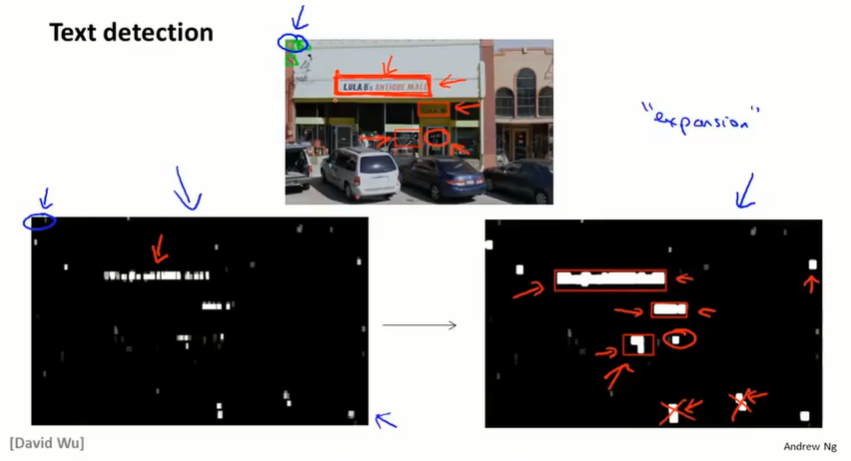
文本检测任务：

模型训练阶段，也可以训练类似的监督学习模型：

预测阶段：使用小的滑动窗口，预测图中各个区域有文字的概率（越亮代表有文字的可能性大）然后进行放大算子，将白色区域扩大。并对长宽比进行筛选。

pipeline第二步：字母分割

训练监督学习模型，识别字母分割的部分

在第一步检测到文字的区域进行滑动窗口，预测在哪里进行了字母的分割。

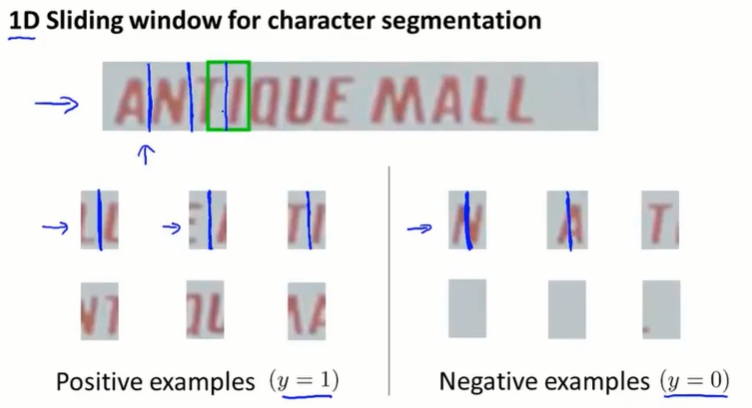
pipeline第三步：字母识别

监督学习多分类问题，不赘述。

18.3 获取大量数据和人工数据合成（getting lots of data : artificial data synthesis）

一个得到高性能机器学习系统的方法：做一个低偏差的机器学习算法，并且使用庞大的训练集去训练它。

通过人工数据合成，得到大量的训练数据。

其一：从零开始产生数据集

用不同的字体生成字符，然后粘贴到不同的背景下，应用模糊算子、仿射变换、缩放旋转等操作，制作成为新的训练样本。

左边是真实数据集，右边是人造数据集。

从已有数据扩充数据集

将已有数据样本进行扭曲等操作，扩充数据集。在语音识别中，也可以认为给“干净”的音频加上各种背景噪声，扩充数据集。

注意，要添加“有意义”的噪声，即在真实异常状况下会出现的噪声。添加纯净的随机噪声往往是没用的。比如最好改变文字的形状，只加高斯噪声改变图片某处的亮度没什么用。

其他

扩充数据集有用吗？在扩充数据集之前，首先要保证我们的分类器偏差较低。这样，更多的数据才会起作用。标准的做法是绘制学习曲线，确保这是低偏差、高方差的分类器。如果分类器的偏差太高，可以尝试增加特征的数量，或者增加神经网络隐藏神经元的数量，直到偏差降低。然后再花精力生成人工训练集。
获得10倍于当前数据集的数据，需要花费多少努力？其实扩充数据集没有想象中难。
- 本节讲的，人工生成
- 收集数据或打标签
- 众包

18.4 上限分析：劲往何处使（ceiling analysis : what part of the pipeline to work on next）

工作流中的哪一部分是最值得花时间去研究的？

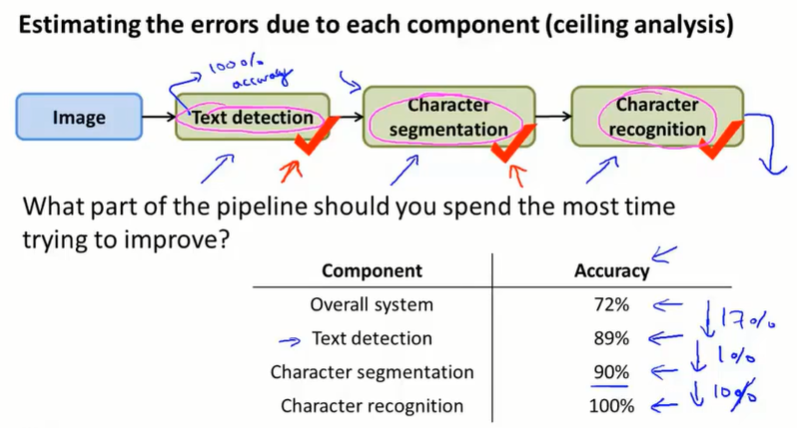
对学习系统使用一个数值评价度量：准确度accuracy。先看整个系统的表现（72%），然后人工按顺序给出每个模块的正确答案，然后看整个系统的准确度表现提升。这样，我们可以看出各个模块的上升空间有多大。

如图，就算 character segmentation 模块到达了完美，总体性能也只能提升 1%。

另一个例子，身份识别的pipeline如下：

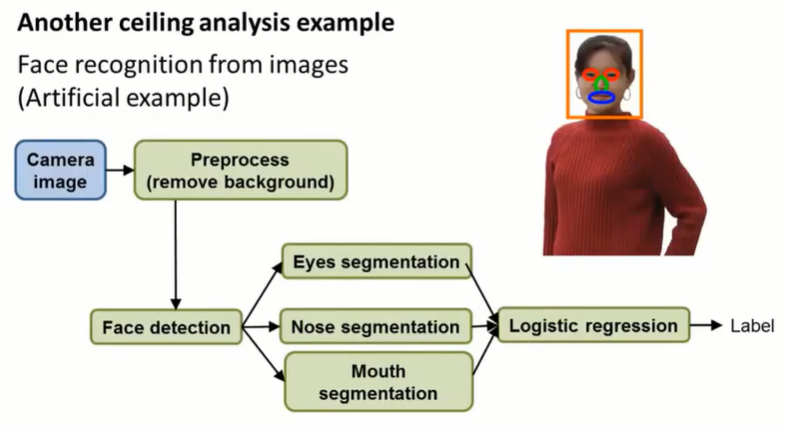
上限分析如下：

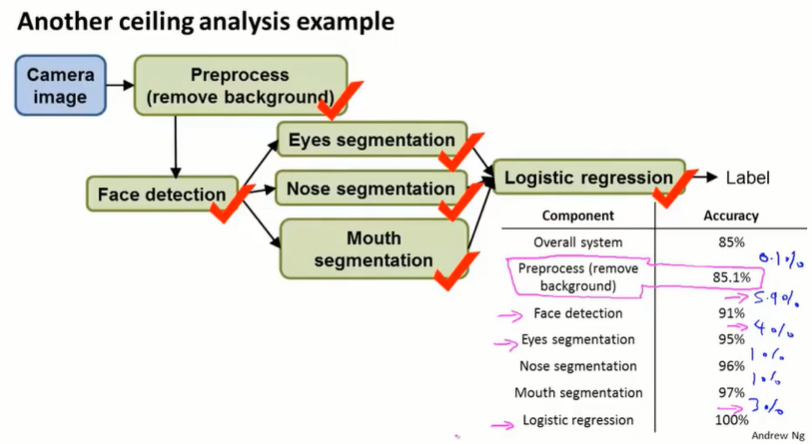
可以看到，完美的 face detection、eyes segmentation、logistic regression 会对模型有较大的改进；preprocess 对模型的改进很小。

第一章 引言