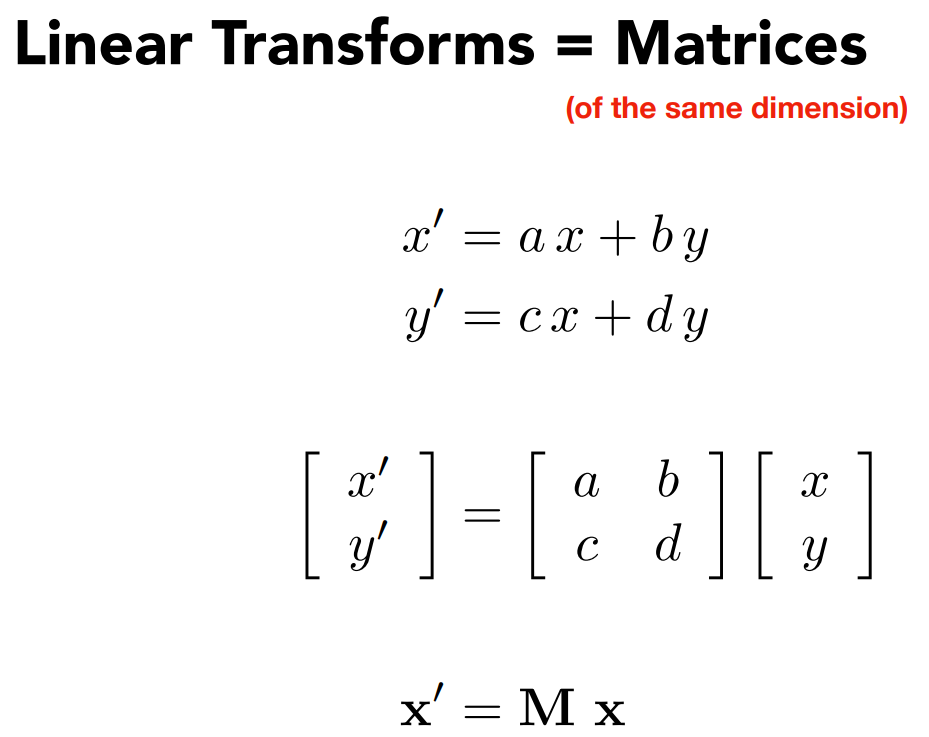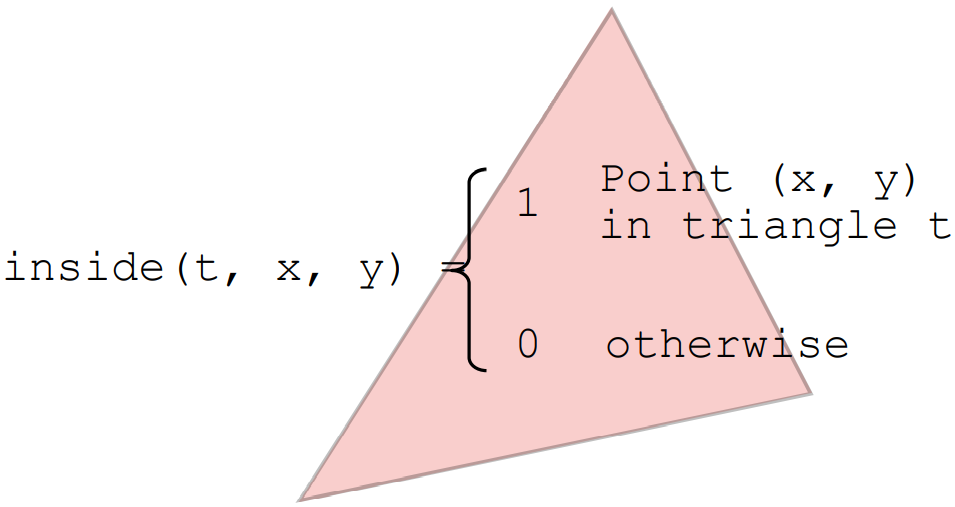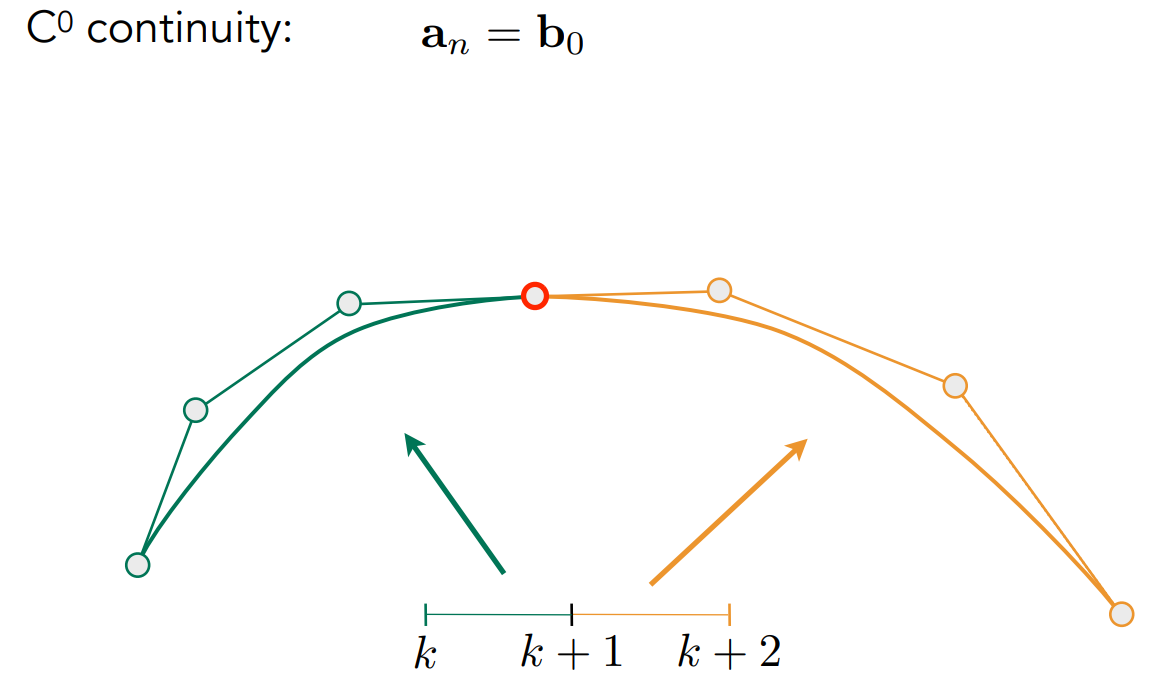早在两年前毕业后的暑假,我就尝试学了一下GAMES101,到第三课矩阵变换的地方就败北了。今年,为了补一补游戏开发的基础知识,才终于坚持着全看完,断断续续用了一个半月。两年过去了,一些概念和计算理解起来也容易了。
我想这应该是我上过的最好的中文课了吧?首先干货很多,不仅讲各种经典方法,还讲到了“现代”的发展,期间还有很多的支线专题、基础知识;然后听起来很舒适,很课会给我“秀>教”的感觉,但GAMES101没有。图形学很难、很交叉,能有闫令琪这种强度的人,制作这么好的中文入门课程,我感到由衷的感激。
笔记已经全部回顾并精心整理了。之前有一些开发工作,没有多余的脑子做作业,后面做完了作业再总结一下吧。
Lecture 01 - Overviews of Computer Graphics
1 - 引入
图形学的应用
游戏:
- 游戏中,如何评价画面好不好?
- 画面亮,说明全局光照做得好,看起来更舒服
- 《无主之地3》卡通渲染中的卡通是什么样的风格,怎么做?
影视:
电影中的特效(special effects)属于图形学的一部分,是最简单的图形学应用
- 特效是在日常生活看不到的,不会产生违和感
- 最困难的是日常生活最常见的东西
《阿凡达》把人的面部捕捉做得很好
动画:
- 《疯狂动物城》的每根毛发都被渲染出来,每根头发都跟光线进行作用
- 图形学的几何(毛发的表示)、渲染(计算光照并显示)
- 《冰雪奇缘2》各种技能是怎样做出来的,风吹动衣服、头发如何运动
- 图形学中的模拟/动画
设计:
CAD(Computer-Aided Design),给汽车建模并实时切换光照查看效果
- 几何(汽车的各个面)、光照(计算不同光照的效果)、模拟(模拟车撞墙的实验)
家装网站,渲染室内设计图片
其他:
可视化,将各种视觉信息展现出来,是图形学的重大应用
VR/AR
数字绘画(Photoshop)
仿真/模拟/动画/特效
GUI
字体设计,矢量图和点阵
图形学的挑战
基础挑战:
图形学是创建逼真的虚拟世界并与之交互(Creates and interacts with realistic virtual world)
输入:研究好真实世界的所有方面的规律,才能将真实世界表示清楚
输出:使用新的计算方法、显示设备、显示技术
技术挑战:
- Math of (perspective) projections, curves, surfaces
- Physics of lighting and shading
- Representing / operating shapes in 3D
- Animation / simulation
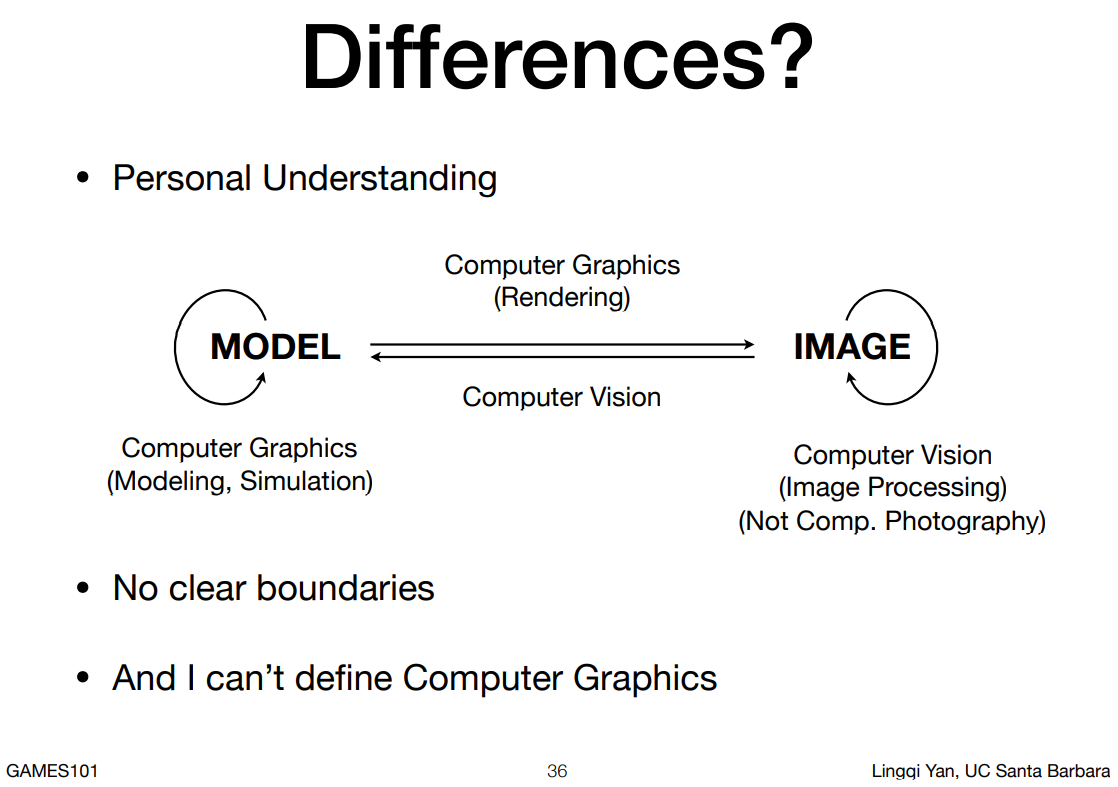
CG和CV
- CV:需要计算机进行猜测;希望计算机分析、理解
- CG:创建世界
图形学依赖于
- 基础数学 - 线性代数、微积分、统计
- 基础物理 - 光学、力学
- 其他 - 信号处理、数值分析(渲染的整个过程就是在解一个递归定义的积分;模拟/仿真很多是在解有限元问题和扩散方程)
- 一些美感
2 - 具体内容
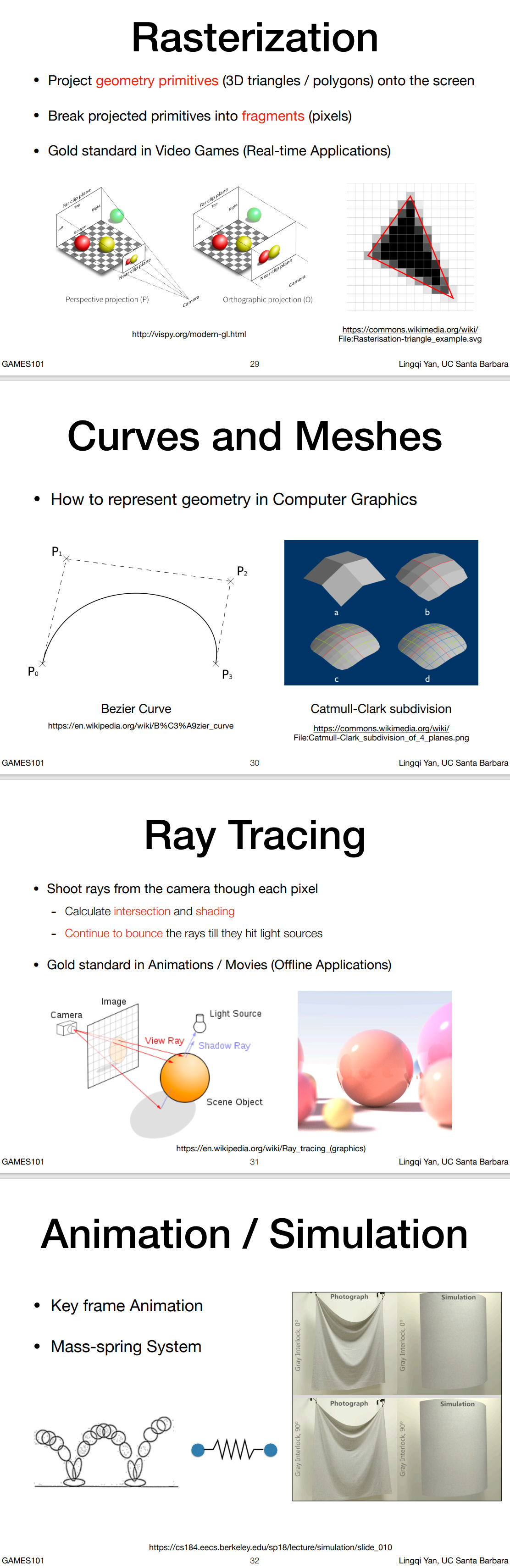
Rasterization
光栅化:把3D空间的几何形体显示在屏幕上。是实时计算机图形学的主要应用
- 实时:30fps级别
- OpenGL,Shader等是如何运作的
Curves and Meshes
如何表示曲线和曲面,如何细分曲面,形变时如何变化等
Ray Tracing
光线追踪常用于动画、电影等离线的场合,较慢但生成质量更高的画面,注意两者的trade-off
Animation / Simulation
动画,各种模拟的效果
Lecture 02 - Review of Linear Algebra
1 - Vectors(向量)
基本概念
- 写作 $\vec a$ 或 $\bold a$ ,或用起点和终点表示为 $\overrightarrow{AB} = B - A$
- 是一个矢量,有方向和长度两个属性,表示向量的方向和数值大小
- 没有绝对的开始位置,平移后仍然是同一个向量,只看相对位置
Vector Normalization
- 向量的长度:$||\vec a||$
- 单位向量 $\hat a$
- 长度是 1
- 找到任意向量的单位向量(normalization):$\hat a=\vec a / ||\vec a||$
- 通常作为图形学中方向的表示方法,只关心它的方向、不关心长度
向量加法
- 在几何意义上,向量相加可以联想平行四边形法则(起点相同)或三角形法则(首尾相连)
- 在代数意义上,向量相加就是直接把坐标相加
Cartesian Coordinates
在笛卡尔坐标系中,默认向量起点从零点开始,可以只用两个数就表示一个向量
- $\bf A = \begin{pmatrix}x\\y\end{pmatrix}$,图形学中默认一个向量是列向量
$\bold {A} ^T = (x, y)$
$||\bold A|| = \sqrt{x^2+y^2}$
$\vec a + \vec b = (x_1+x_2, y_1+y_2)$
向量乘法
向量点乘
$\vec a \cdot \vec b = ||\vec a||\ ||\vec b||\cos \theta$ ,向量点乘的结果是一个数
计算向量夹角
- $\cos \theta = \frac{\vec a \cdot \vec b}{||\vec a||\ ||\vec b||}$
- 对于单位向量,$\cos \theta = \hat a \cdot \hat b$
性质
- 交换律:$\vec a \cdot \vec b = \vec b \cdot \vec a\ $
- 结合律:$(k\vec a)\cdot \vec b = \vec a \cdot (k\vec b) = k(\vec a\cdot\vec b)$
- 分配律:$\vec a \cdot(\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c$
笛卡尔坐标系中的向量点乘,就是对应元素相乘再加起来
- 2D:$\vec a \cdot \vec b=\begin{pmatrix} {x_a}\\{y_a} \end{pmatrix} \cdot \begin{pmatrix} {x_b}\\{y_b} \end{pmatrix} = x_ax_b + y_ay_b$
- 3D:$\vec a \cdot \vec b=\begin{pmatrix} {x_a}\\{y_a}\\{z_a} \end{pmatrix} \cdot \begin{pmatrix} {x_b}\\{y_b}\\{z_b} \end{pmatrix} = x_ax_b + y_ay_b + z_az_b$
点乘在图形学中的应用
- 找到两个向量间的夹角,如光线和物体表面的夹角
- 找到一个向量在另一个向量上的投影,如计算阴影
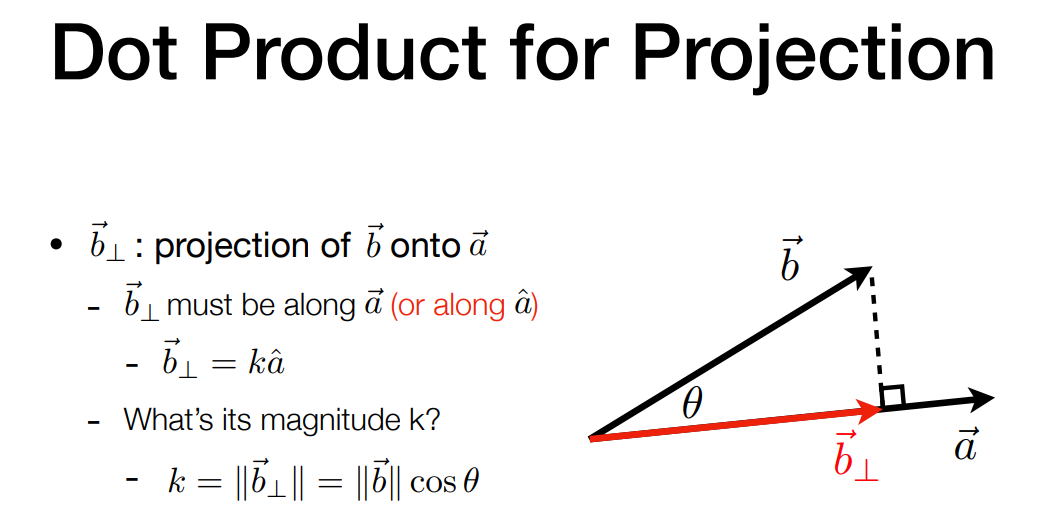
- 计算 $\vec b$ 在 $\vec a$ 上的投影
- 方向跟 $\vec a$ 相同,$\vec {b_\perp}= k\hat a$
- 长度 $k = ||\vec {b_\perp}|| = ||\vec {b}\cos \theta||$
- 计算 $\vec b$ 在 $\vec a$ 上的投影
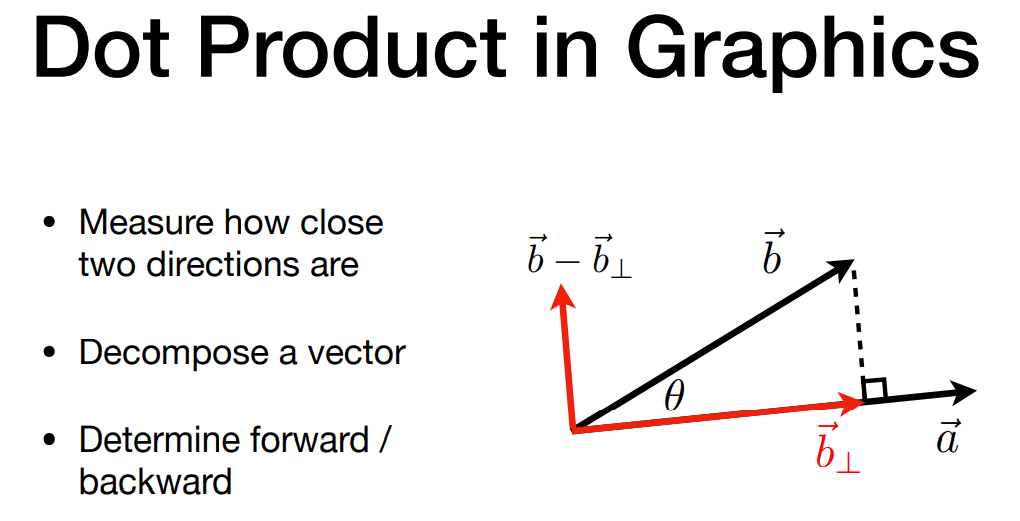
- 在向量投影基础上的计算
- 在垂直、平行方向分解一个向量
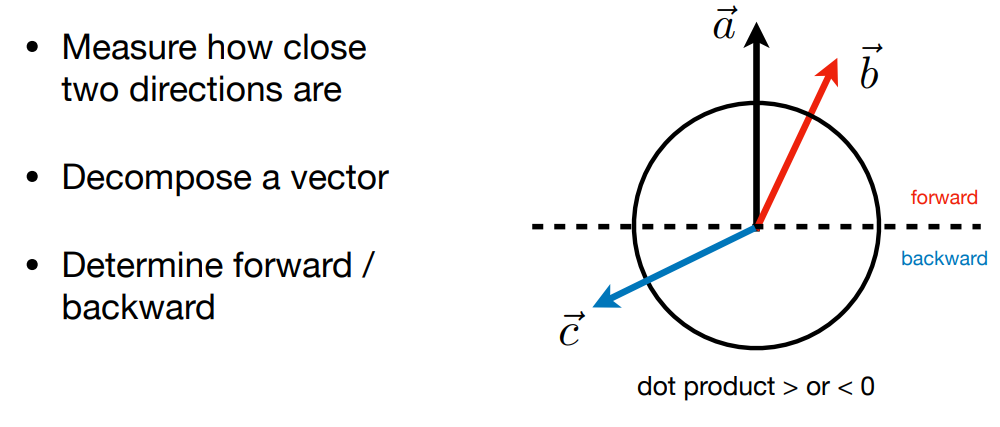
- 计算两个向量的 “接近” 程度:点乘的结果大,说明夹角小
- 可用于判断是否能看到镜面反射、高光等
- 点乘的符号表示向量 “前”与“后” 的信息:点乘的结果为负,两个向量方向基本相反
向量叉乘
向量叉乘的结果是一个向量
- 方向垂直于 $\vec a$ 和 $\vec b$ 所在的平面,具体方向根据右手螺旋定则确定
- $\vec a \times \vec b=-\vec b\times \vec a$ ,不满足交换律
- $||\vec a \times \vec b|| = ||\vec a||\ ||\vec b||\sin \phi$
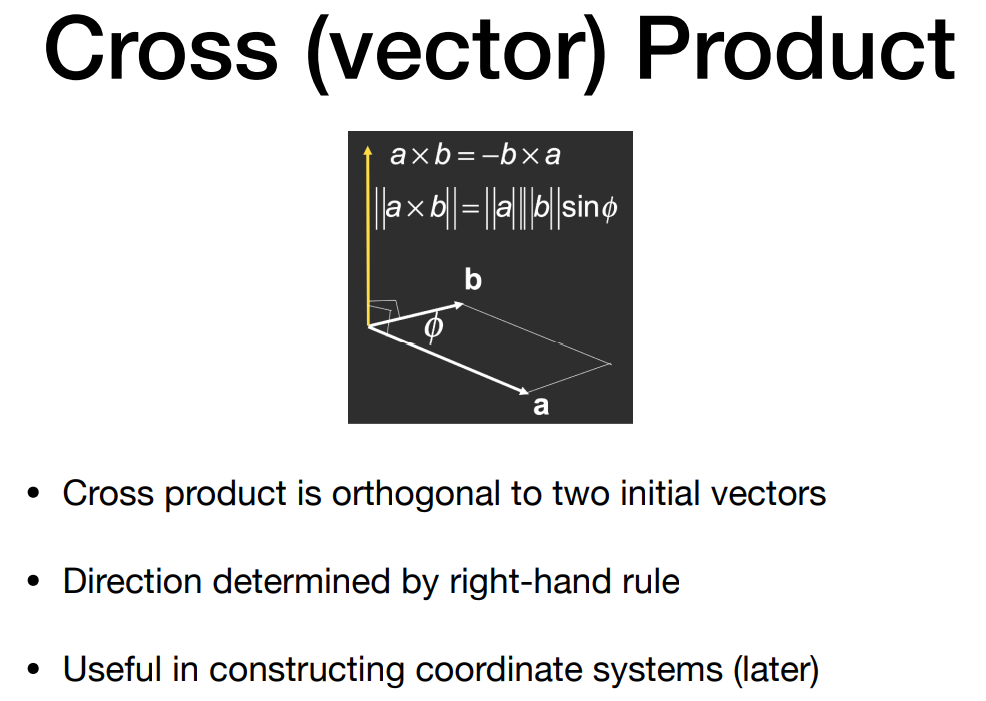
- 方向垂直于 $\vec a$ 和 $\vec b$ 所在的平面,具体方向根据右手螺旋定则确定
性质
- 可以确定一个三维坐标系,如果满足 $\vec x \times \vec y = +\vec z$,就是右手坐标系
- 计算性质
- 满足分配律、结合律,不满足交换律
- 向量叉乘自己,$\sin \phi=0$,得到的是零向量
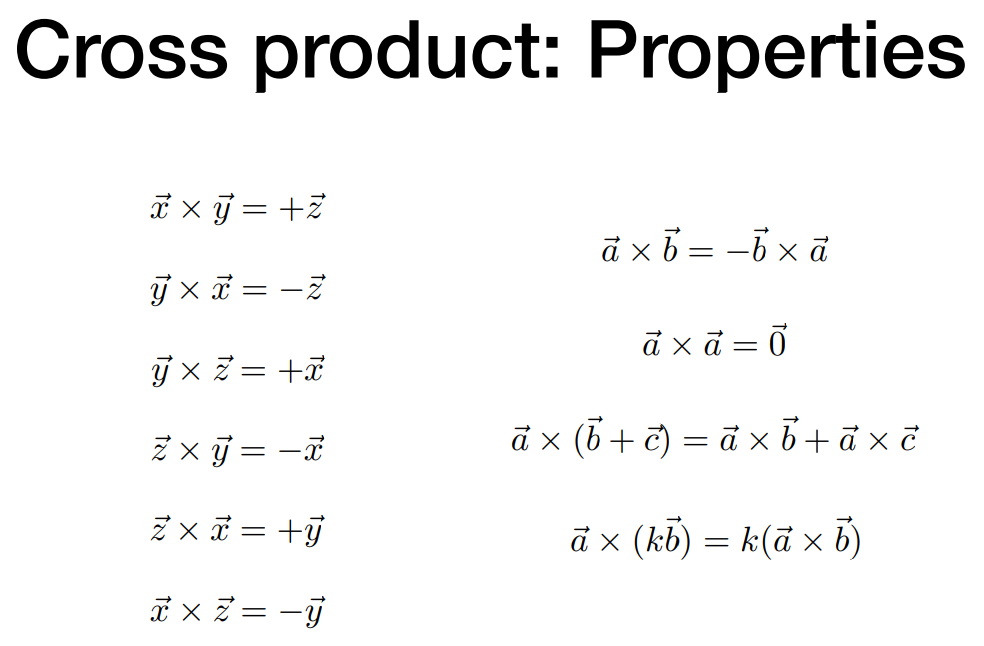
计算,向量坐标形式和矩阵乘法形式
- 注意图中向量的对偶矩阵(dual matrix),它跟向量有同样的叉乘意义

叉乘在图形学中的应用
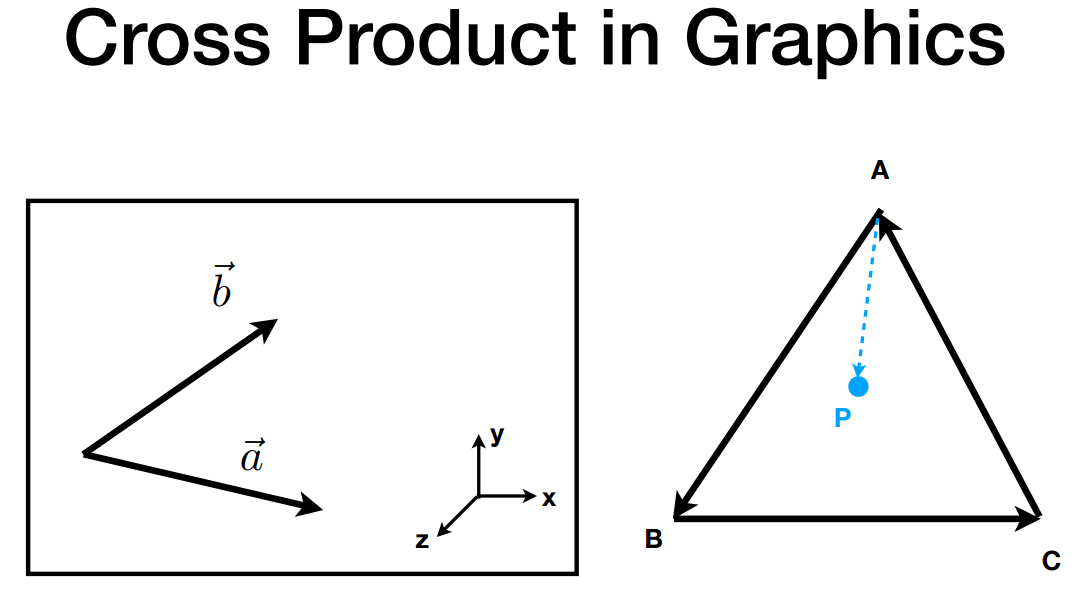
- 判定 “左”和“右”
- 右手系中,叉乘 $\vec a \times \vec b$ 是正向量,说明 $\vec b$ 在 $\vec a$ 的左侧
- 左手系中,叉乘 $\vec a \times \vec b$ 是正向量,说明 $\vec b$ 在 $\vec a$ 的右侧
- 判定 “内”和“外”
- 点 $P$ 是否在三角形内部?$\overrightarrow {AB} \times\overrightarrow {AP}$ 结果向外,说明 $P$ 在 $\overrightarrow {AB}$ 的左侧,同理判断 $P$ 点跟三条边的位置关系
- 检查 $P$ 点是否一直在所有边的同一边,从而确定 $P$ 点是否在多边形的内部
- 这是三角形光栅化的基础,判断三角形覆盖了哪些像素、进而对像素进行着色
- 如果刚好同方向(叉乘结果是零向量),对于corner case可以自行处理
- 判定 “左”和“右”
定义一个正交坐标系
- 三个坐标轴互相垂直
- 任意向量 $\vec p$ 可以对应到坐标系中的三个轴上(使用投影计算长度)
- $\vec p = (\vec p\cdot\hat u)\hat u + (\vec p\cdot\hat v)\hat v + (\vec p\cdot\hat w)\hat w$
2 - Matrices(矩阵)
基本概念
把一些数组合成一个 $m \times n$ 的结构
在图形学中,矩阵普遍被用于表示变换(移动、旋转、缩放、剪切)
矩阵乘法
- 矩阵的行列需要匹配,才能相乘;$(M\times N)(N\times P)=(M\times P)$
- 对于相乘后矩阵的每个值,可以这样计算:$(i, j)$ 位置的值是 $A$ 矩阵第 $i$ 行和 $B$ 矩阵第 $j$ 列的两个向量的点积
- 没有任何交换律;满足结合律和分配律
矩阵和向量相乘
- 始终认为:矩阵在左、向量在右且是列向量,$(M\times N)(N\times 1)=(M\times 1)$
- 如:进行 $x$ 轴镜像变换的矩阵 $\begin{pmatrix} -1&0\\0&1 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix} = \begin{pmatrix} -x\\y \end{pmatrix}$
其他
矩阵转置
- $\begin{pmatrix} 1&2\\3&4 \\ 5&6 \end{pmatrix} ^T = \begin{pmatrix} 1&3&5\\2&4&6\end{pmatrix}$
$(AB)^T = B^T A^T$
单位矩阵、逆矩阵
- $I_{3\times 3} = \begin{pmatrix} 1&0&0\\0&1&0 \\ 0&0&1 \end{pmatrix}$ ;单位矩阵本身不做操作,主要定义逆矩阵
- $AA^{-1}= A^{-1}A = I$
- $(AB)^{-1} = B^{-1}A^{-1}$
3 - 向量乘法的矩阵表示
点乘
叉乘
Lecture 03 - Transformation
1 - 变换的应用
为什么学习变换、2D变换(旋转/缩放/切变)、齐次坐标、变换的组合、3D变换
- 模型变换
- 视图变换
- IK(位置改变时,反推模型的变换)
- 光栅化过程(3D到2D的投影)
2 - 二维空间的变换
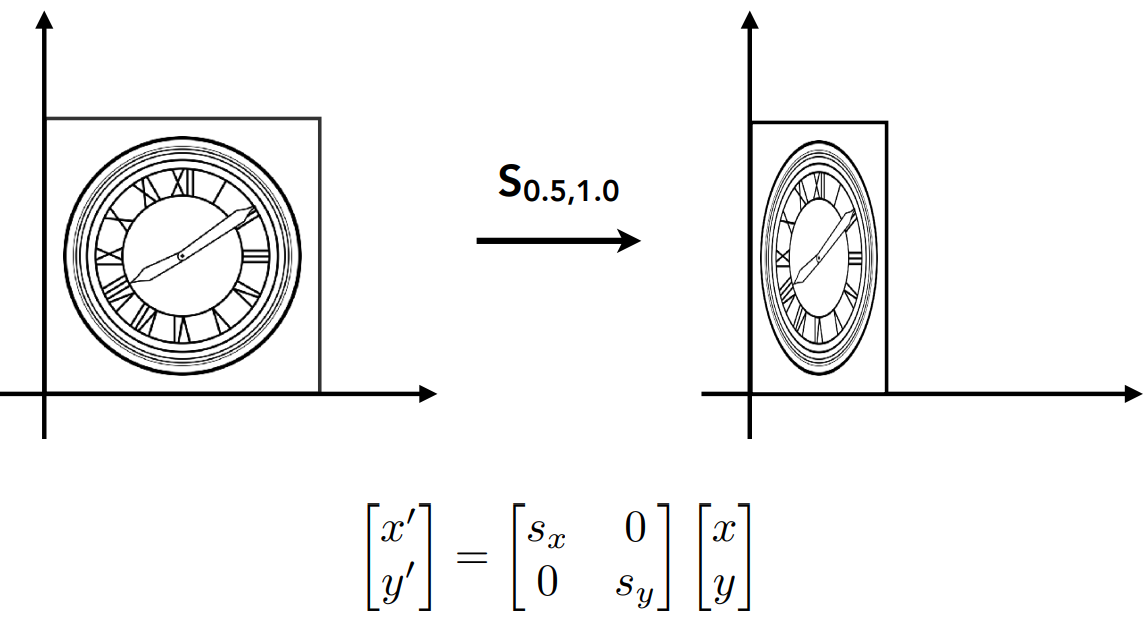
Scale
- $\left \{ \begin{array}{l} x' = s_xx \\ y' = s_yy \end{array} \right.$
- $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x&0 \\ 0&s_y \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}$
Reflection
- $\left \{ \begin{array}{l} x' = -x \\ y' = y \end{array} \right.$
- $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1&0 \\ 0&1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}$
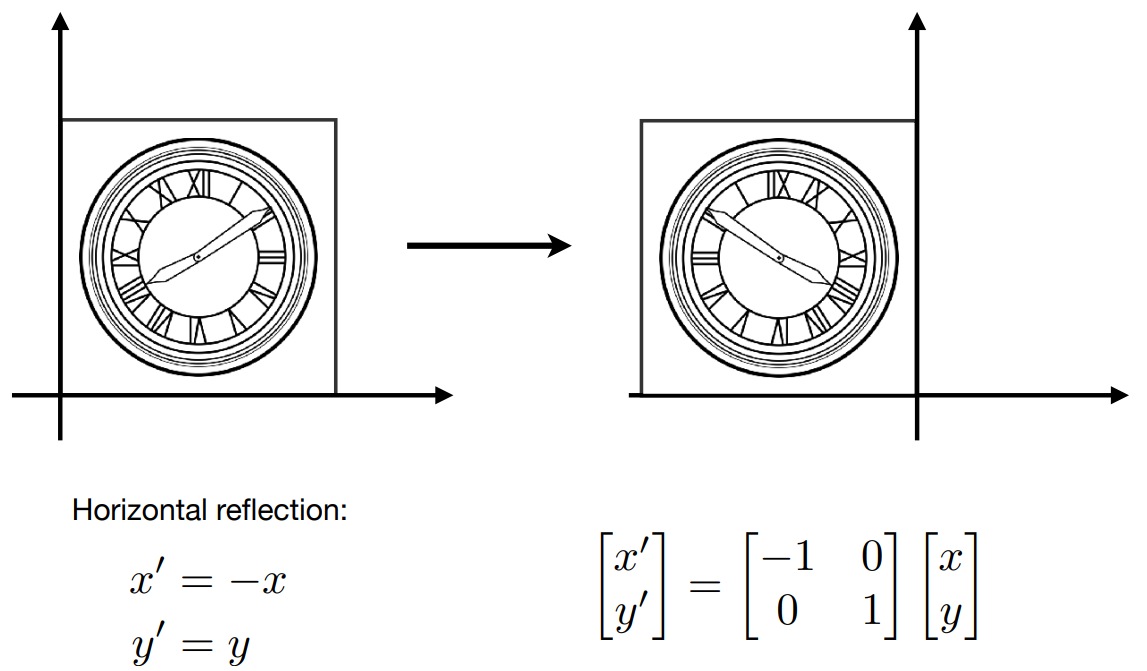
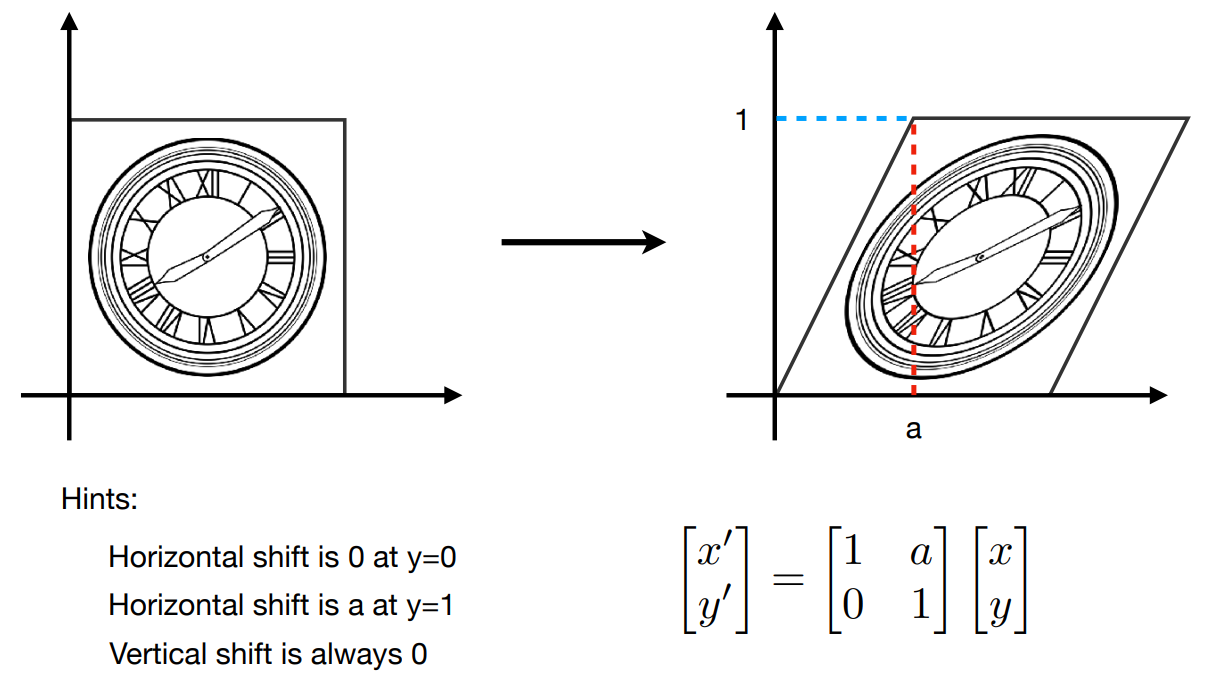
Shear
- $\left \{ \begin{array}{l} x' = x+ay \\ y' = y \end{array} \right.$
- $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1&a \\ 0&1 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}$
Rotate (about the origin (0, 0), CCW by default)
- $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta&-\sin\theta \\ \sin\theta&\cos\theta \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}$
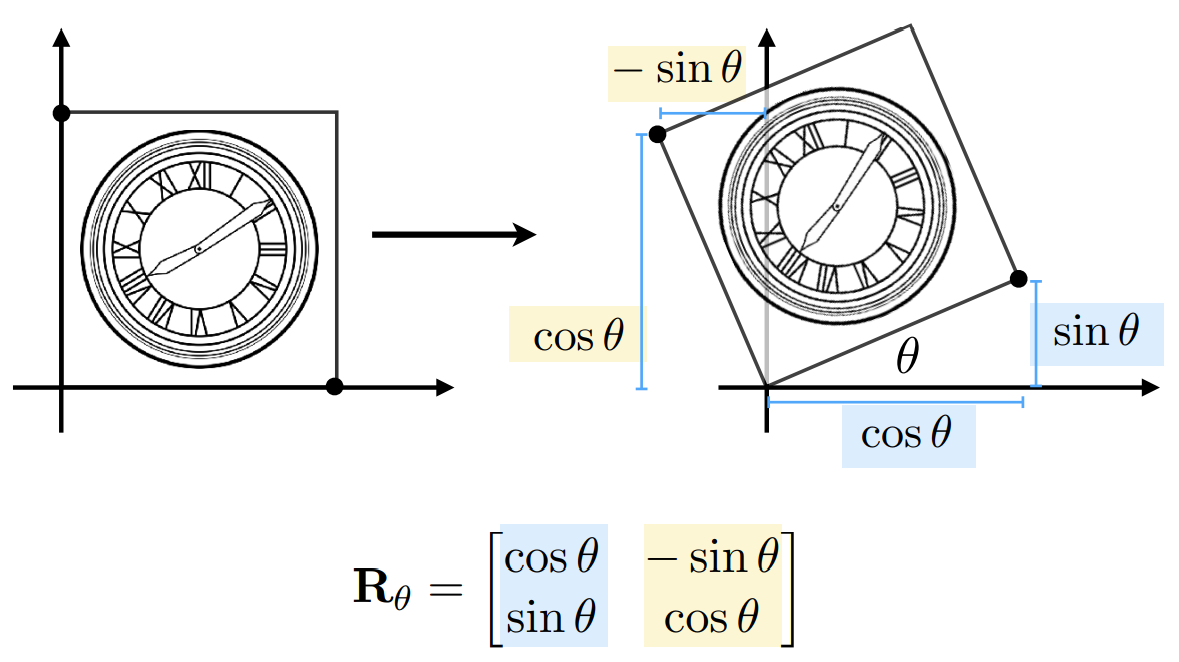
推导方法:
- 设 $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a&b \\ c&d \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}$ ,即 $\left \{ \begin{array}{l} x' = ax+by \\ y' = cx+dy \end{array} \right.$
- 带入 $\left \{ \begin{array}{l} (1, 0)\rightarrow (\cos\theta, \sin\theta) \\ (0, 1)\rightarrow (-\sin\theta, \cos\theta) \end{array}\right.$ 两个变换关系
- 解得 $\left \{ \begin{array}{l} a = \cos\theta \\ b = -\sin\theta \\ c = \sin\theta\\d = \cos\theta \end{array} \right.$
- $R_\theta =\begin{pmatrix}\cos\theta &-\sin\theta \\\sin\theta & \cos\theta \end{pmatrix}$,$R_{-\theta} =\begin{pmatrix}\cos\theta &\sin\theta \\-\sin\theta & \cos\theta \end{pmatrix}$
旋转矩阵是正交矩阵
- 计算上,旋转 $-\theta$ 的矩阵就是旋转 $\theta$ 的转置
- 从定义上看,旋转 $-\theta$ 正好是旋转 $\theta$ 的逆操作
- 即:旋转中,旋转矩阵的逆就是旋转矩阵的转置,称这个矩阵为正交矩阵
- $R_{-\theta}=R_{\theta}^{-1}$
几种变换的共同点
都是线性变换:能写成 矩阵×坐标 的形式。
3 - Homogeneous coordinates(齐次坐标)
为了更方便地表示非线性变换,引入齐次坐标的概念。
特殊的变换:Translation
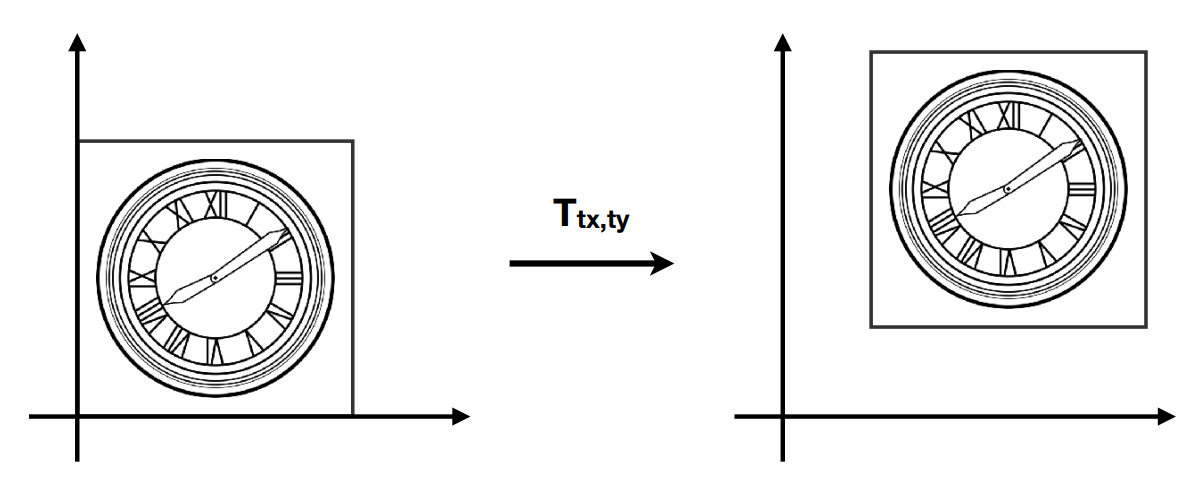
- $\left \{ \begin{array}{l} x' = x+t_x \\ y' = y+t_y \end{array} \right.$
平移变换不属于线性变换的范畴,无法写成之前的矩阵相乘的形式
- $\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a&b \\ c&d \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}$
不想将平移变换当成一个特殊的变换,有没有办法表示所有的变换?(注意,trade-off或者NFL定律表明,引入齐次坐标同样会带来问题)
Homogeneous Coordinates(齐次坐标)
给2D的点和向量都增加第三个维度(w-coordinate)的信息:
- 2D point:$(x, y, 1)^T$
- 2D vector:$(x, y, 0)^T$
用矩阵表示平移变换:
- $ \begin{pmatrix} x'\\y'\\w' \end{pmatrix} = \begin{pmatrix} 1&0&t_x\\0&1&t_y \\ 0&0&1 \end{pmatrix} \cdot \begin{pmatrix} x\\y\\1 \end{pmatrix} = \begin{pmatrix} x+t_x\\y+t_y\\1 \end{pmatrix}$
为什么点的w-coordinate是1,而矩阵是0?
- 解释上,向量具有平移不变性:向量经过上面的平移变换后,可以发现,由于第三维是0,平移对向量不起作用
- 理解上,这也定义了 point 和 vector 之间的一些运算
- vector + vector = vector
- point - point = vector(把1减没了)
- point + vector = point
- point + point = ??
- 在齐次坐标中, $\begin{pmatrix} x\\y\\w \end{pmatrix}$ 就是2D点 $ \begin{pmatrix} x/w\\y/w\\1 \end{pmatrix} ,w\ne 0$
- 因此 point + point = 中点
- 引入齐次坐标,不仅保证了向量的平移不变性,而且保证了运算的正确性
齐次坐标的代价是什么?
- 增加了几个数,但2D仿射变换的最后一行都是 $(0,0,1)$ ,存储简单
Affine Transformations(仿射变换)
定义仿射变换
- affine map = linear map + translation:$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a&b \\ c&d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix}$
- 使用齐次坐标表示:$\begin{pmatrix} x' \\ y' \\1 \end{pmatrix} = \begin{pmatrix} a&b&t_x \\ c&d&t_y \\ 0&0&1\end{pmatrix}\begin{pmatrix} x \\ y \\ 1\end{pmatrix}$
最后一行永远是 $(0,0,1)$,平移永远写在最后一列的前两个数,$a,b,c,d$ 是线性变换
所有的2D仿射变换都写成了 矩阵 × 向量 的形式:
- Scale:$\bold S(s_x, s_y) = \begin{pmatrix} s_x&0&0 \\ 0&s_y&0 \\ 0&0&1\end{pmatrix}$
- Rotation:$\bold R(\alpha)=\begin{pmatrix} \cos\alpha&-\sin\alpha&0 \\ \sin\alpha&\cos\alpha&0 \\ 0&0&1\end{pmatrix}$
- Translation:$\bold T(t_x,t_y)=\begin{pmatrix} 1&0&t_x \\ 0&1&t_y \\ 0&0&1\end{pmatrix}$
4 - Composing Tranforms
Inverse Tranform
一个变换的逆变换,在数学上对应乘以变换矩阵的逆矩阵 $\bold M^{-1}$
变换的组合
一个简单的变换:先旋转再平移
一个复杂的变换可以通过一系列简单的变换组合而成
变换的顺序是重要的(默认旋转绕原点,先平移再旋转就会转到错误的位置)
矩阵不满足交换律
- $R_{45}\cdot T_{(1,0)} \ne T_{(1,0)}\cdot R_{45}$
矩阵的乘法顺序是从右向左
- 先旋转、再平移 $T_{(1,0)}\cdot R_{45}\begin{bmatrix} x \\ y \\ 1\end{bmatrix} = \begin{bmatrix} 1&0&1 \\ 0&1&0 \\ 0&0&1\end{bmatrix} \begin{bmatrix} \cos{45^{\circ}}&-\sin{45^{\circ}}&0 \\ \sin{45^{\circ}}&\cos{45^{\circ}}&0 \\ 0&0&1\end{bmatrix} \begin{bmatrix} x \\ y \\ 1\end{bmatrix}$
推广两个变换到多个变换:
- $A_n(...A_2(A_1(x))) = \bold A_n \cdot \cdot \cdot \bold A_2\cdot \bold A_1 \cdot\begin{pmatrix}x\\y\\1\end{pmatrix}$
应用顺序依然是从右到左
矩阵乘法没有交换律,但满足结合律
- 可以先把 $\bold A_n \cdot \cdot \cdot \bold A_2\cdot \bold A_1 $ 求出一个矩阵,然后把这个矩阵应用到向量
- 求得的这个矩阵依然是一个 3×3 的矩阵,即可以用一个矩阵表示很复杂的变换,变换多了不会让矩阵变复杂
变换的分解
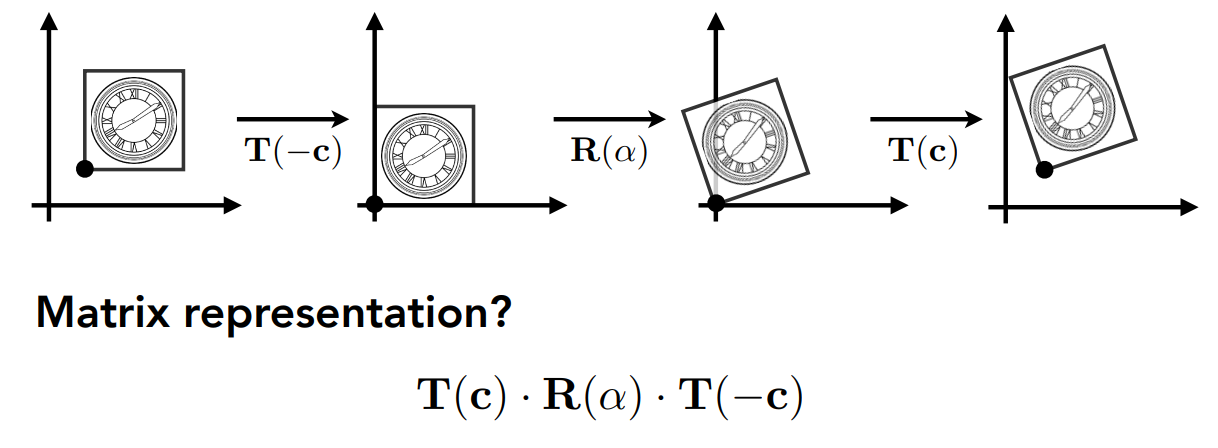
如何绕任意一个点旋转?
- 由于旋转矩阵是绕原点旋转的,不能用单个旋转矩阵表示绕任意一个点旋转的变换
- 先移到原点、再旋转、再平移回去
- 写成矩阵形式,依然是从右到左
5 - 3D Transforms
三维空间的仿射变换
简单扩展之前2D空间的表示方法(homogeneous coordinates)
- 3D point = $(x,y,z,1)^T$
- 3D vector = $(x,y,z,0)^T$
- In general, $(x,y,z,w),w\ne 0$ is the 3D point: $(x/w,y/w,z/w)$
3D Transformations,使用齐次坐标表示:
- $\begin{pmatrix} x' \\ y' \\ z' \\1 \end{pmatrix} = \begin{pmatrix} a&b&c&t_x \\ d&e&f&t_y \\ g&h&i&t_z \\ 0&0&0&1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix}$
- 3×3 的矩阵是 3D 空间的线性变换,最后一列是平移,最后一行永远是 $(0,0,0,1)$
一个问题:这个 4×4 矩阵应用在向量上,平移 和 线性变换 的顺序是什么?
- 先线性变换、再平移
- 回顾2D的情况
- affine map = linear map + translation:$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a&b \\ c&d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_x \\ t_y \end{pmatrix}$
- 而不是 $\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a&b \\ c&d \end{pmatrix}\begin{pmatrix} x+t_x \\ y+t_y \end{pmatrix} $
- 使用 homogeneous coordinates 来表示这个变换:$\begin{pmatrix} x' \\ y' \\1 \end{pmatrix} = \begin{pmatrix} a&b&t_x \\ c&d&t_y \\ 0&0&1\end{pmatrix}\begin{pmatrix} x \\ y \\ 1\end{pmatrix}$
- 在3D中,也是一样的,先应用线性变换、再平移
Lecture 04 - Transformation Cont.
3D变换、Viewing 变换(视图/相机变换,投影变换(正交变换、透视变换))
1 - 3D Transformations
回顾
- 3D point = $(x,y,z,1)^T$
- 3D vector = $(x,y,z,0)^T$
- 齐次坐标表示3D变换:$\begin{pmatrix} x' \\ y' \\ z' \\1 \end{pmatrix} = \begin{pmatrix} a&b&c&t_x \\ d&e&f&t_y \\ g&h&i&t_z \\ 0&0&0&1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix}$ ,先应用线性变换、再加上平移量
3D空间的若干变换
缩放
- Scale:$\bold S(s_x, s_y, s_z) = \begin{pmatrix} s_x&0&0&0 \\ 0&s_y&0&0\\ 0&0&s_z&0 \\ 0&0&0&1 \end{pmatrix}$
平移
- Translation:$\bold T(t_x, t_y, t_z) = \begin{pmatrix} 1&0&0&t_x \\ 0&1&0&t_y\\ 0&0&1&t_z \\ 0&0&0&1 \end{pmatrix}$
旋转
绕 $x, y, z$ 轴旋转
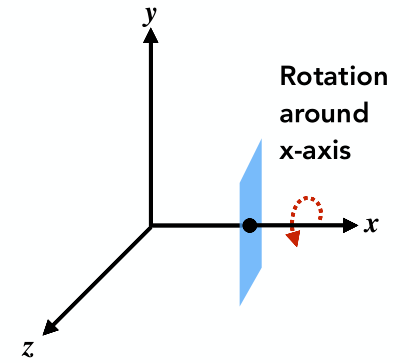
绕哪个轴旋转,对应的坐标就不会改变
- $\bold R_x(\alpha) = \begin{pmatrix} 1&0&0&0 \\ 0&\cos\alpha&-\sin\alpha&0\\ 0&\sin\alpha&\cos\alpha&0 \\ 0&0&0&1 \end{pmatrix}$
- $\bold R_y(\alpha) = \begin{pmatrix} \cos\alpha&0&\sin\alpha&0 \\ 0&1&0&0\\ -\sin\alpha&0&\cos\alpha&0 \\ 0&0&0&1 \end{pmatrix}$ ,注意到是 $\vec z\times \vec x = \vec y$,跟 $x$ 和 $z$ 轴是相反的
- $\bold R_z(\alpha) = \begin{pmatrix} \cos\alpha&-\sin\alpha&0&0 \\ \sin\alpha&\cos\alpha&0&0\\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix}$
由 $\bold R_x,\bold R_y,\bold R_z$ 组合的旋转
- 定义 $\bold R_{xyz}(\alpha,\beta,\gamma)=\bold R_x(\alpha)\bold R_y(\beta)\bold R_z(\gamma)$
- $\alpha,\beta,\gamma$ 称为欧拉角
- 对应飞机上下抬头(Pitch),左右转向(Yaw),歪过来转(Roll)
任意旋转
- Rodrigues' Rotation Formula:$\bold R(\bold n, \alpha) = \cos(\alpha)\bold I + (1- \cos(\alpha))\bold{nn}^T +\sin\alpha \underbrace{\begin{pmatrix} 0&-n_z&n_y \\ n_z&0&-n_x \\ -n_y&n_x&0\end{pmatrix}}_{\bold N} $
- 这个矩阵是向量 $n$ 的对偶矩阵,查看第二课向量叉乘部分,对偶矩阵理解为一个向量的矩阵表示形式
- 罗德里格斯旋转公式表达了绕任意旋转轴 $\bold n$ 旋转任意角度 $\alpha$ 的变换。注意,用一个向量 $\bold n $ 表示这个旋转轴,即默认这个轴过原点
- 如何过任意轴旋转?结合上节2D旋转的做法,先平移到过原点的轴旋转、再进行罗德里格斯旋转、再平移回去
四元数的概念:为了旋转之间的插值而提出的概念。旋转矩阵是不适合作为插值的,四元数可以跟旋转矩阵互相转化、并解决这个问题。
2 - Viewing 的概念
Viewing 分为 View/Camera Transformation(视图变换) 和 Projection Tranformation(投影变换),可以通过现实生活中拍照的过程来理解:
- 找到好位置,摆姿势:model transformation 模型变换
- 摄像机找好角度:view transformation 视图变换
- 拍照:projection transformation 投影变换
3 - Viewing 之 View / Camera Transformation
如何定义一个相机?
- 相机的位置 $\vec e$
- 相机看向的方向 $\hat g$
- 相机的上方向 $\hat t$
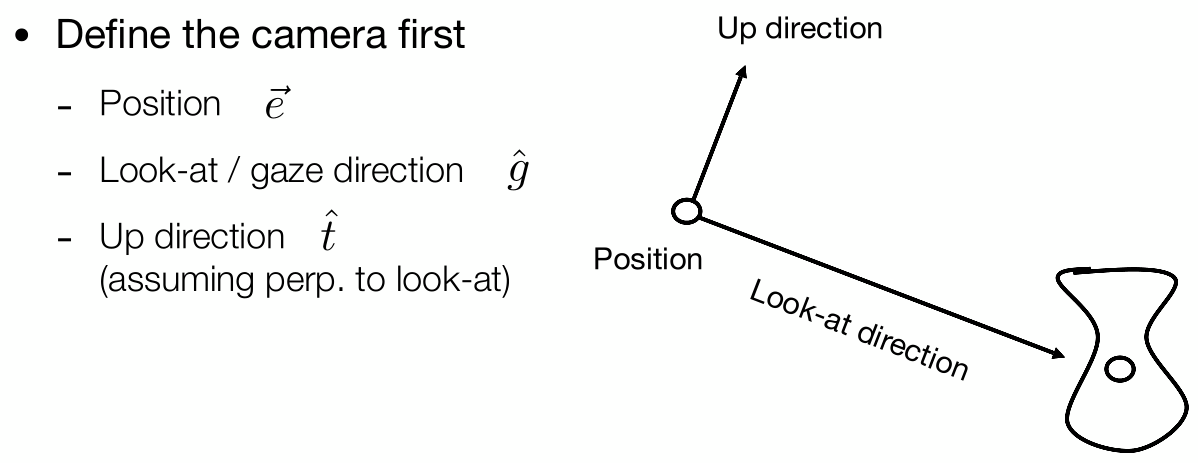
相机的特性:跟物体、环境相对运动一致时,得到的结果相同
因此,为了简化操作,把相机放在标准位置上:
- 位于原点,朝 $-z$ 方向看,向上方向是 $y$
- 其他物体随着相机移动
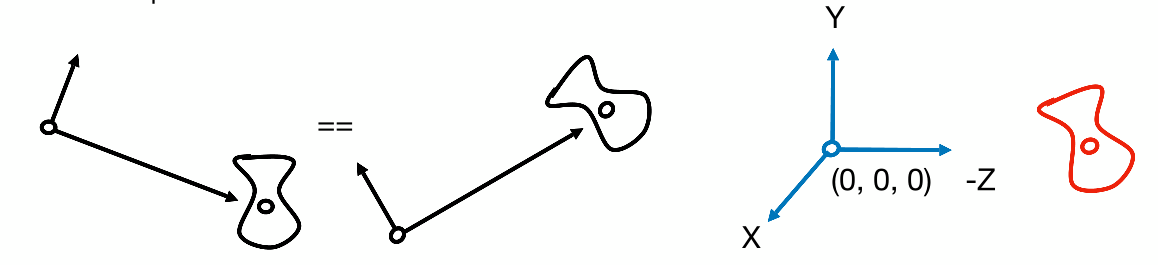
进行相机标准化变换 $M_{view}$
- 原本相机在 $\vec e$ ,看向 $\hat g$ ,上方向 $\hat t$ ;目标相机在 $0$,看向 $-Z$,上方向 $Y$
- 平移 $\vec e$ 到 $(0,0,0)$
- 观察方向 $\hat g$ 旋转到 $-Z$
- 上方向 $\hat t$ 旋转到 $Y$
- $\hat g\times \hat t$ 旋转到 $X$
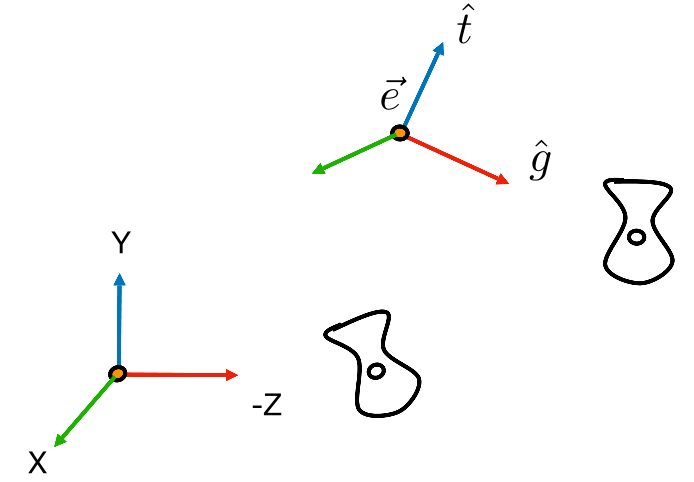
写成矩阵形式
$M_{view}=R_{view}T_{view}$ ,先平移再旋转(齐次坐标本来就是这样)
- 平移到原点:$T_{view}=\begin{bmatrix}1&0&0&-x_e \\ 0&1&0&-y_e \\ 0&0&1&-z_e \\ 0&0&0&1 \end{bmatrix}$
旋转到正确方向,直接旋转不好写,但从目标方向旋转到原方向好些
逆旋转:$X \rightarrow \hat g\times\hat t$,$Y\rightarrow \hat t$,$Z\rightarrow -\hat g$
计算方法:带入 $(1,0,0) \rightarrow \hat g\times\hat t$,$(0,1,0)\rightarrow \hat t$,$(0,0,1)\rightarrow -\hat g$
- $R^{-1}_{view}=\begin{bmatrix}x_{\hat g\times \hat t}&x_t&x_{-g}&0 \\ y_{\hat g\times \hat t}&y_t&y_{-g}&0 \\ z_{\hat g\times \hat t}&z_t&z_{-g}&0 \\ 0&0&0&1 \end{bmatrix}$
结合第三课中,旋转矩阵的性质:旋转矩阵是正交矩阵,逆旋转变换的矩阵是旋转矩阵的转置,得到旋转矩阵
- $R_{view}=\begin{bmatrix}x_{\hat g\times \hat t}&y_{\hat g\times \hat t}&z_{\hat g\times \hat t}&0 \\ x_t&y_t&z_t&0 \\ x_{-g}&y_{-g}&z_{-g}&0 \\ 0&0&0&1 \end{bmatrix}$
由 $M_{view}=R_{view}T_{view}$,得到相机的视图变换
其他物体也跟相机一起做相同的变换,也称为 Model View Transformation(模型视图变换)
4 - Viewing 之 Projection transformation
透视投影的两种方式
Orthographic projection:正交投影,常用于工程制图,不体现近大远小
Perspective projection:透视投影,鸽子为什么这么大
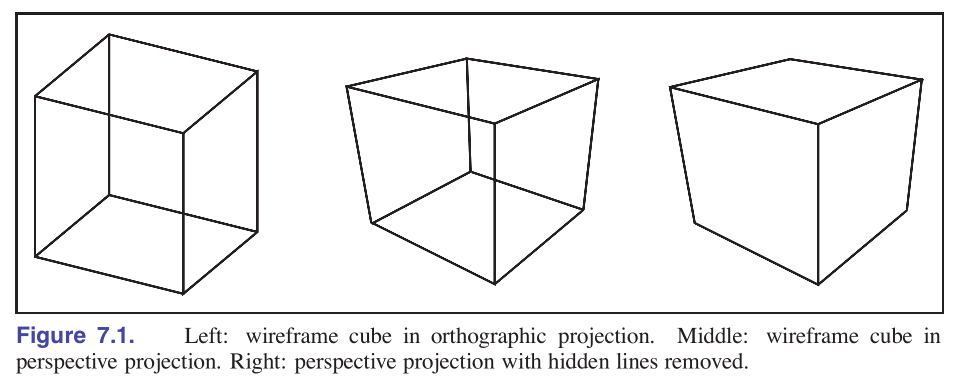
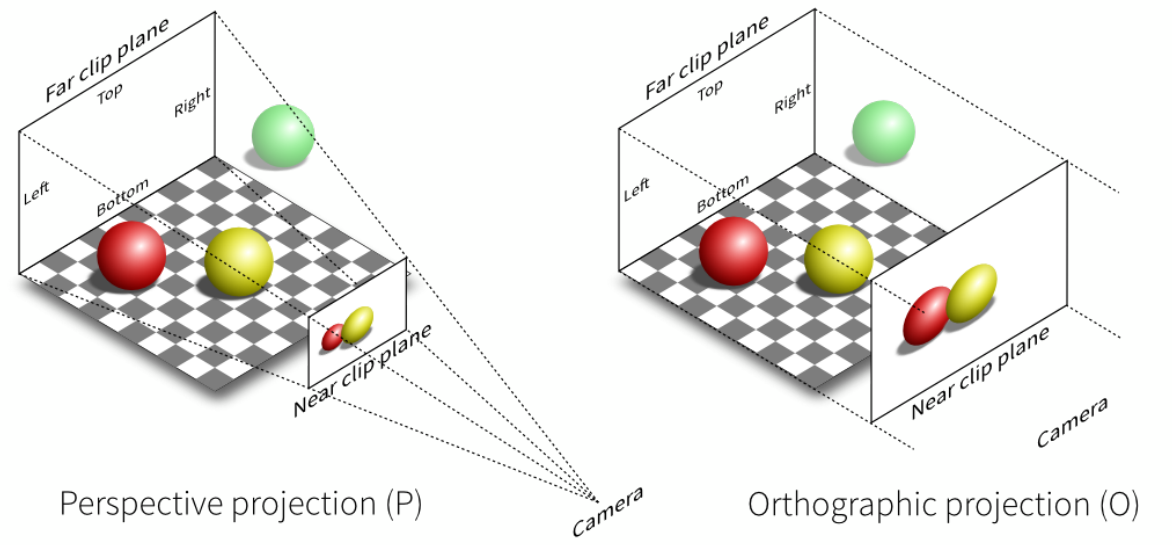
Orthographic Projection
简单理解的做法
- 相机位于原点,看向 $-Z$,上方向 $Y$
- 丢掉 $Z$ 坐标,得到 $X,Y$ 平面上的图
- 标准化到 $[-1, 1]$

图形学的做法
- 用三个轴各一个区间,定义一个3D空间的立方体 $[l,r]\times [b,t]\times [f,n]$
- left, right, bottom, top, far, near
- 由于右手坐标系、沿着 $-Z$ 方向看,导致 far < near
- OpenGL等左手系在此处更容易理解,但带来 $X \times Y \ne Z$
- 将这个立方体映射到 canonical(正则、规范、标准) 立方体 $[-1,1]^3$
- 具体做法:把立方体的中点移动到原点,然后把三个轴都标准化到 $[-1,1]$
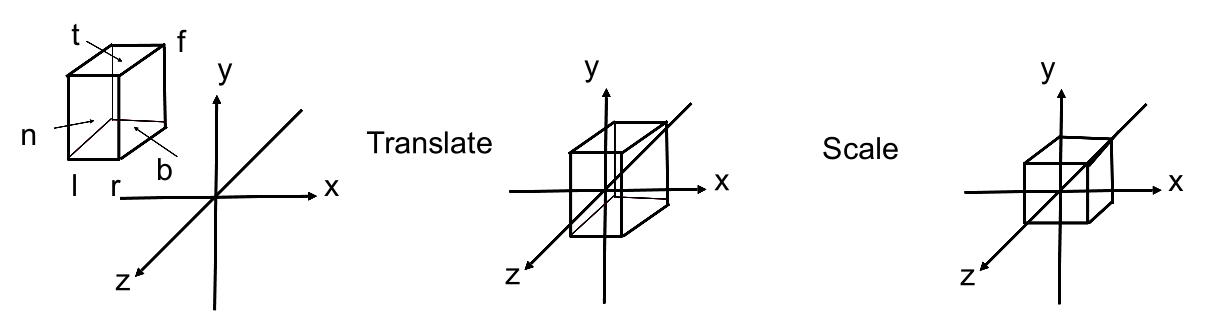
- $M_{ortho}=\begin{bmatrix}\frac{2}{r-l}&0&0&0 \\ 0&\frac{2}{t-b}&0&0 \\ 0&0&\frac{2}{n-f}&0 \\ 0&0&0&1 \end{bmatrix} \begin{bmatrix}1&0&0&-\frac{r+l}{2} \\ 0&1&0&-\frac{t+b}{2} \\ 0&0&1&-\frac{n+f}{2} \\ 0&0&0&1 \end{bmatrix}$
- 写成齐次坐标的变换矩阵形式
- 先把中点平移到 $(0,0,0)$,然后把三个轴覆盖的长度都变为 $2$,对应 $[-1,1]$
- 做完这个变换,所有的物体都会位于$[-1,1]^3$ 并被拉伸,在之后会做视口变换让它们恢复正常的形状
Perspective Projection
透视投影的步骤
- 回顾:
- $(x,y,z,1)$,$(kx,ky,kz,k\ne0)$,$(zx,zy,z^2,z\ne0)$ 都表示3D中的同一个点 $(x,y,z)$
- 如 $(1,0,0,1)$ 和 $(2,0,0,2)$ 表示同一个点
- 透视投影中,把一个平面投影到另一个平面上,透视投影变换就是把两个屏幕对应点的映射关系

- 一种方法是直接求左图线表示的映射关系
- 另一种方法:先把左图的形状“挤压”成右图的矩形体($M_{persp\rightarrow ortho}$),然后对于矩形体应用之前的正交投影
- 在第一步操作下,near平面上的点不会变化,其他平面上的中心点也不会发生变化
- 由于相机位于原点、过原点的直线延申得来两个平面,可以构建相似三角形
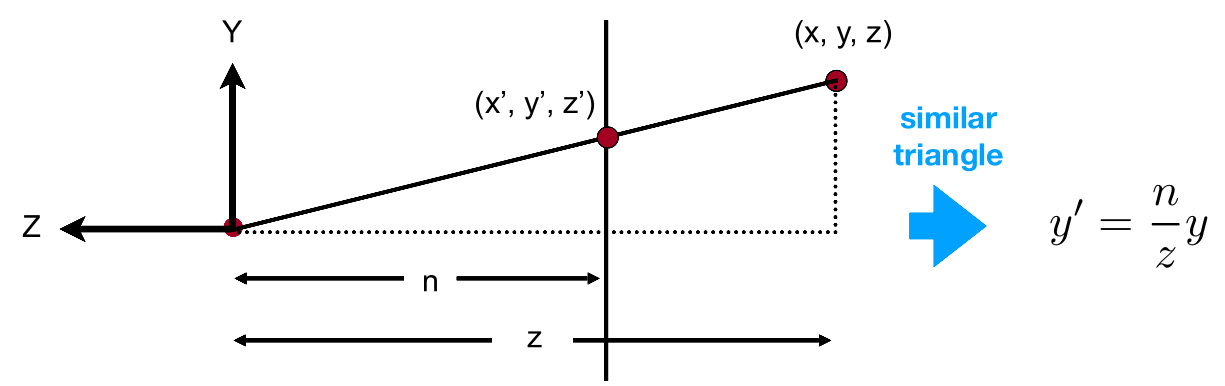
- 由相似三角形,可以得出任意一点 $(x,y,z)$ 挤压到 $(x’,y’,z’)$ 的计算方法 $y’=\frac{n}{z}y,x’=\frac{n}{z}x$
- $z’\ne z$。除了near和far面的其他面,挤压过程中 $z$ 会发生变化,但目前不清楚变化方式
- 对于相似三角形,我的理解:
- 这个图有一个误导: $(x,y,z)$ 经过挤压变成了near平面上的 $(x’,y’,z’)$
- 事实上:相似三角形展示了 $x$ 和 $y$ 在挤压中的变化方式,也就是经过挤压,都会跟near平面的 $x’,y’$ 相同,并且对于每个 $x,y$ 都是如此,可以看上面的挤压图中的连线
- 也就是相似三角形并不展示 $z$ 的变化,$(x,y,z)$ 平移到下方 $y’$ 高度上的某个点,而不是平移到 $(x’,y’,n)$
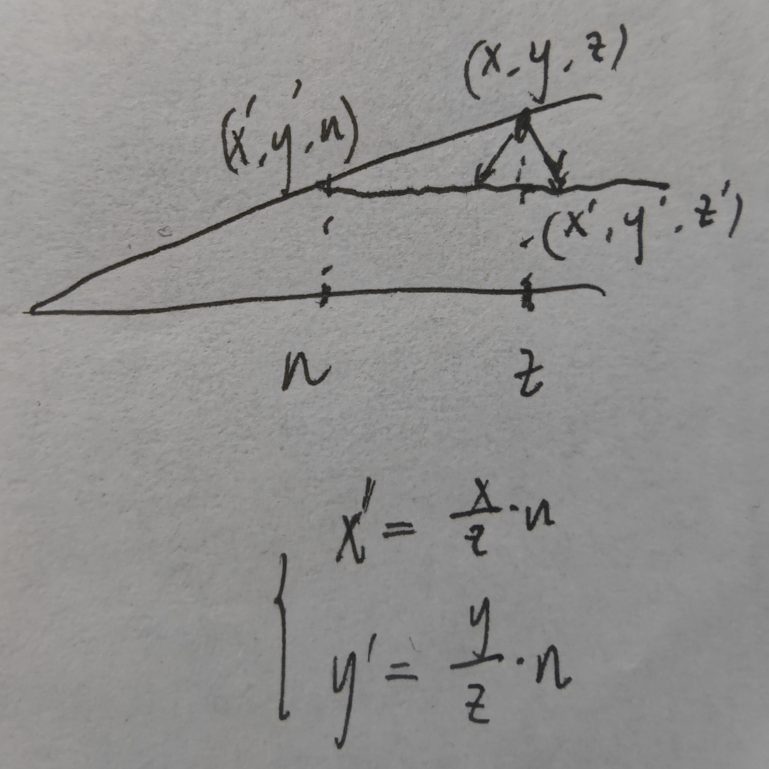
计算“挤压”的变换矩阵
- 以齐次坐标表示每个点“挤压”的变化:$\begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix} \rightarrow \begin{pmatrix} nx/z \\ ny/z \\ \text{unknown} \\ 1\end{pmatrix} ==\begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z\end{pmatrix}$
- 使用到之前说的,乘一个数依然是同一个点
- “挤压”的变换矩阵的作用就是:$M_{persp->ortho}^{(4\times 4)}\begin{pmatrix} x \\ y \\ z \\ 1\end{pmatrix} = \begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z\end{pmatrix}$
- 目前可求得:$M_{persp->ortho}^{(4\times 4)}=\begin{pmatrix}n&0&0&0 \\ 0&n&0&0 \\ ?&?&?&? \\ 0&0&1&0 \end{pmatrix}$
- 这不是仿射变换,最后一行不一定是 $(0,0,0,1)$。在这里是 $(0,0,1,0)$
已知 near 和 far 两个平面的变换关系
- 在 near 平面上的任意点,运算完后不会发生任何变化,$\begin{pmatrix} x \\ y \\ n \\ 1\end{pmatrix} \rightarrow \begin{pmatrix} x \\ y\\ n\\1\end{pmatrix} ==\begin{pmatrix} nx \\ ny\\ n^2\\n\end{pmatrix}$
- 因此,矩阵的第三行 $\begin{pmatrix}A&B&C&D\end{pmatrix} \begin{pmatrix}x\\y\\n\\1\end{pmatrix} = n^2$ ,得 $\left \{ \begin{array}{l} A = 0 \\ B=0 \\Cn+D=n^2 \end{array} \right.$
- 在 far 平面上的任意点,运算完后 $z$ 不会发生变化,$\begin{pmatrix} x \\ y \\ f \\ 1\end{pmatrix} \rightarrow \begin{pmatrix} nx/f \\ ny/f\\ f\\1\end{pmatrix} ==\begin{pmatrix} nx \\ ny\\ f^2\\f\end{pmatrix}$
- 或者 far平面的中心点,运算完后不发生任何变化,$\begin{pmatrix} 0 \\ 0 \\ f \\ 1\end{pmatrix} \rightarrow \begin{pmatrix} 0 \\ 0\\ f\\1\end{pmatrix} ==\begin{pmatrix} 0 \\ 0 \\ f^2\\f\end{pmatrix}$
- 矩阵第三行 $\begin{pmatrix}0&0&C&D\end{pmatrix} \begin{pmatrix}x\\y\\f\\1\end{pmatrix} = f^2$ ,得 $\left \{ \begin{array}{l} A = 0 \\ B=0 \\Cf+D=f^2 \end{array} \right.$
- 联立 $\left \{ \begin{array}{l} Cf+D=f^2 \\Cn+D=n^2 \end{array} \right.$ ,得 $\left \{ \begin{array}{l} C=n+f \\D=-nf \end{array} \right.$
- $M_{persp->ortho}^{(4\times 4)}=\begin{pmatrix}n&0&0&0 \\ 0&n&0&0 \\ 0&0&n+f&-nf \\ 0&0&1&0 \end{pmatrix}$
- 一点思考:$M_{persp->ortho}\begin{pmatrix}x\\y\\z\\1\end{pmatrix} =\begin{pmatrix}nx\\ny\\nz+fz-nf\\z\end{pmatrix}=\begin{pmatrix}nx/z\\ny/z\\n+f-nf/z\\1\end{pmatrix} $
- $z\rightarrow n+f-\frac{nf}{z}$,求解一元二次方程(见草稿纸)后发现,在“挤压”变换中 $z$ 变小(被推向far)
- 也可以直接带几个数进去算
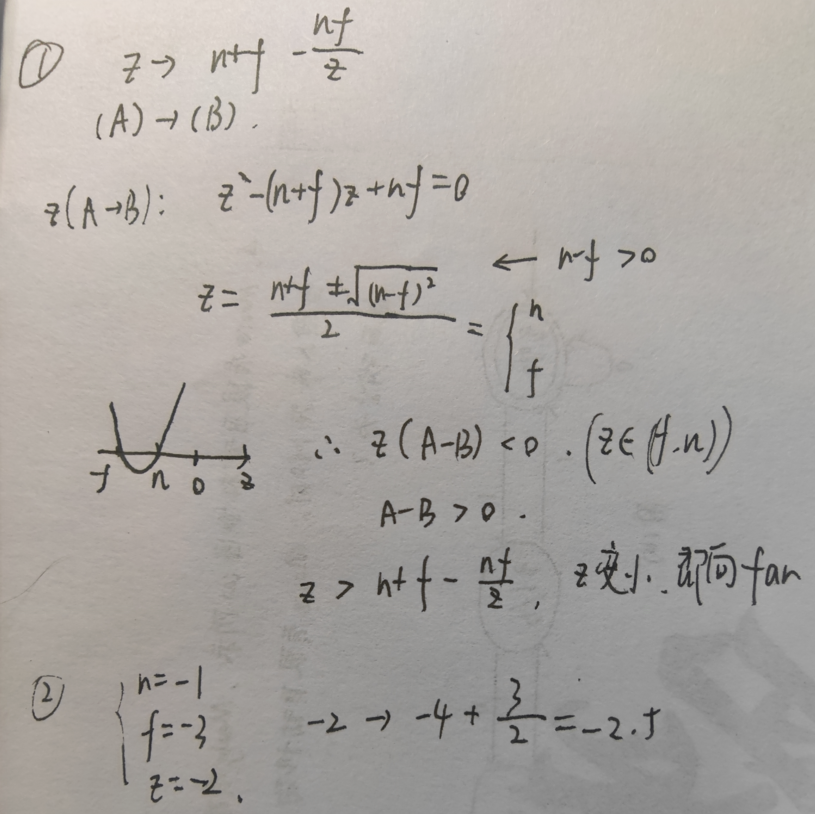
完整的 Perspective Projection
Lecture 05 - Rasterization 1 (Triangles)
上节课讲的是MVP的过程:
- Model Transformation,放置物体
- View Transformation,相机移动到原点、其他物体一起移动
- Projection Transformation,物体投影到 $[1-,1]^3$ 的立方体空间中
- Orthograpic Projection
- Perspective Projection
MVP后,场景中的所有物体都可以投影到 $[1-,1]^3$ 的立方体空间中。下一步该做什么?
将物体画在屏幕上,这一步叫光栅化(Rasterization)。
1 - 透视投影其他
如何定义一个透视投影的frustum
- 可以指定 near,far 平面分别的 left,right,bottom,top
- 也可以用相机的两个参数指定一个平面
- vertical field-of-view:相机垂直可视角度
- aspect ratio:一个平面的宽高比
- 有这两个值,当然也可以得到 horizontal fov
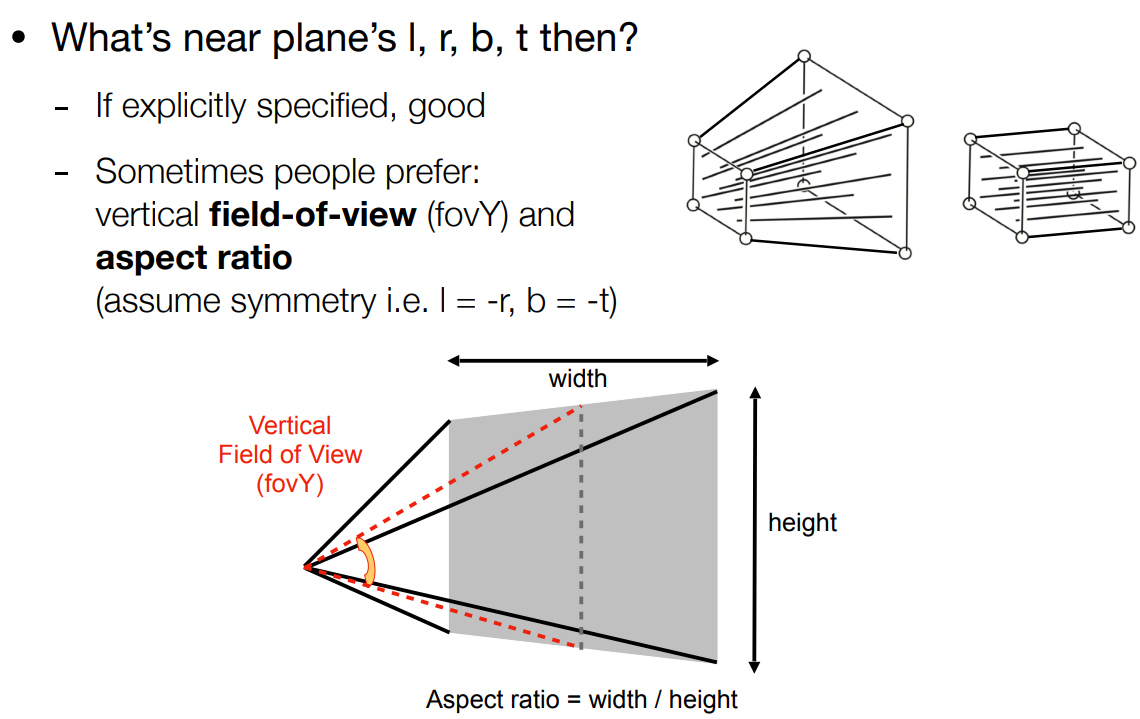
- 有了这两个概念,也可以转换到 left,right,bottom,top
- 通过下图的两个关系,可以求得 top、right,进而求得 bottom、left(假设是中心对称的)
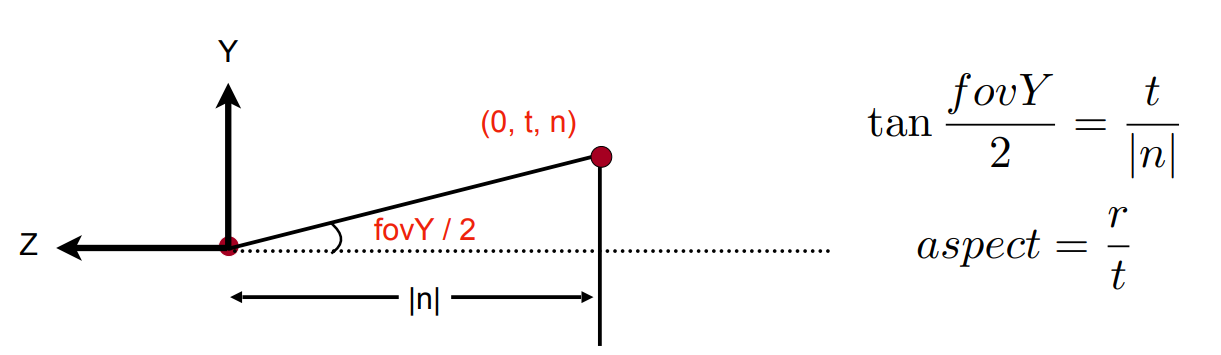
2 - 视口变换(把立方体画在屏幕上)
概念理解
屏幕
- 屏幕是一个二维数组,存的是像素
- pixel 是 picture element 的缩写
- 在本课中,把 pixel 抽象理解成一个小方块,是颜色划分的最小单位
- 一个像素内只有唯一的颜色,用RGB表示
- 数组的大小:分辨率,如 1920×1080
- 屏幕是一个典型的光栅成像设备(raster display)
- raster == screen in German
- rasterize == 把东西画在屏幕上
屏幕空间(定义方法跟虎书有点差别)
- 屏幕左下角是原点,右、上分别是 $x$,$y$ 方向
- 像素坐标定义为 $(x, y)$ ,所有的像素从 $(0,0)$ 到 $(\text{width}-1,\text{height}-1)$
- 用整数的坐标来描述像素,但像素的中心是 $(x+0.5, y+0.5)$
- 整个屏幕的像素覆盖的坐标范围从 $(0,0)$ 到 $(\text{width},\text{height})$
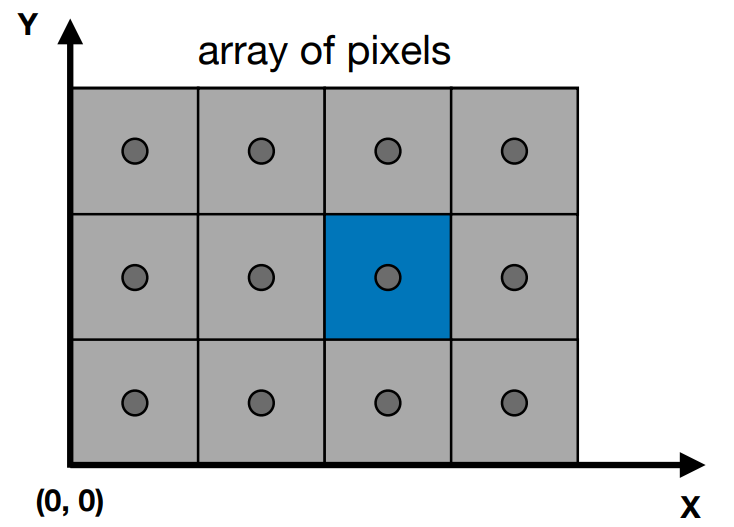
视口变换
需要做的是:从$[-1,1]^3$ 到 $[0,\text{width}]\times[0,\text{height}]$ 的转换
- 先不管 $z$,先做从$[-1,1]^2$ 到 $[0,\text{width}]\times[0,\text{height}]$
$x,y$ 方向的长度先从 2 都 scale 到 width、height,再平移到 width、height 的中点
这里是从中点在原点,平移到左下角在原点,因此是正的
- $M_{viewport}=\begin{pmatrix}\frac{\text{width}}{2}&0&0&\frac{\text{width}}{2} \\ 0&\frac{\text{height}}{2}&0&\frac{\text{height}}{2} \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix}$
这个变化称为视口变换 Viewport Transformation。做完这一步后,3D空间任意物体的 $x,y$ 都在2D屏幕上了
得到了2D空间的物体,下一步需要把物体打散成像素,真正画在屏幕上。
3 - 光栅化(Rasterizing)
光栅显示设备介绍
Oscilloscope,示波器
- 成像原理:跟阴极射线管(Cathode Ray Tube)电视机原理相同,电子发射后经过偏转、打在屏幕上的某个位置;配合隔行扫描等优化技术
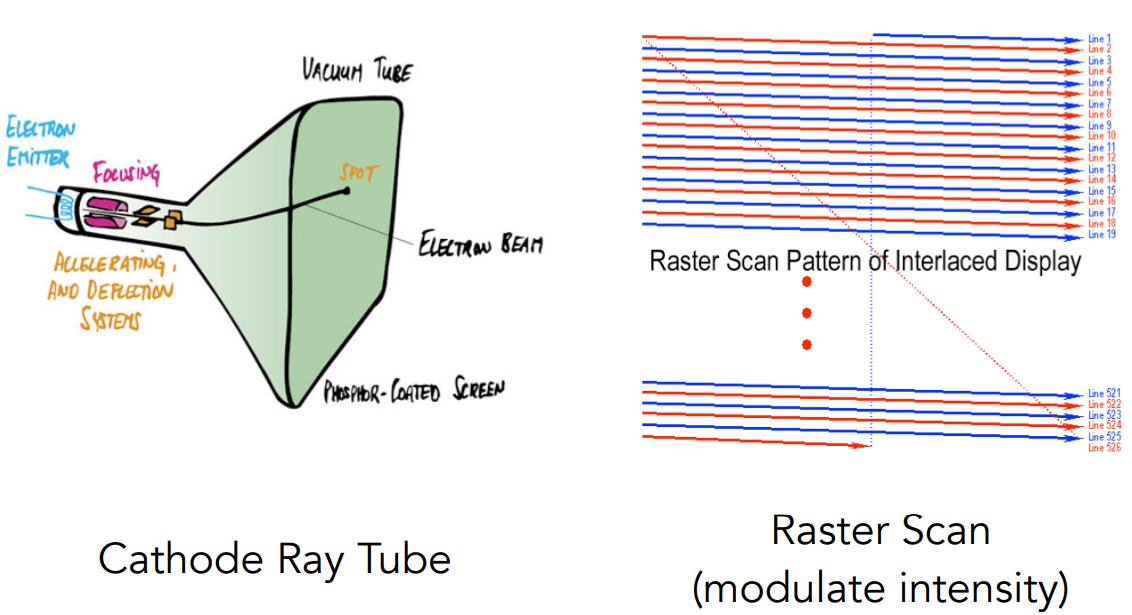
Frame Buffer:显示内存中的一块区域
- 显卡内存的一块区域映射到屏幕上。也可以生成不同图像,存在显存不同区域,然后指定显示器显示哪张
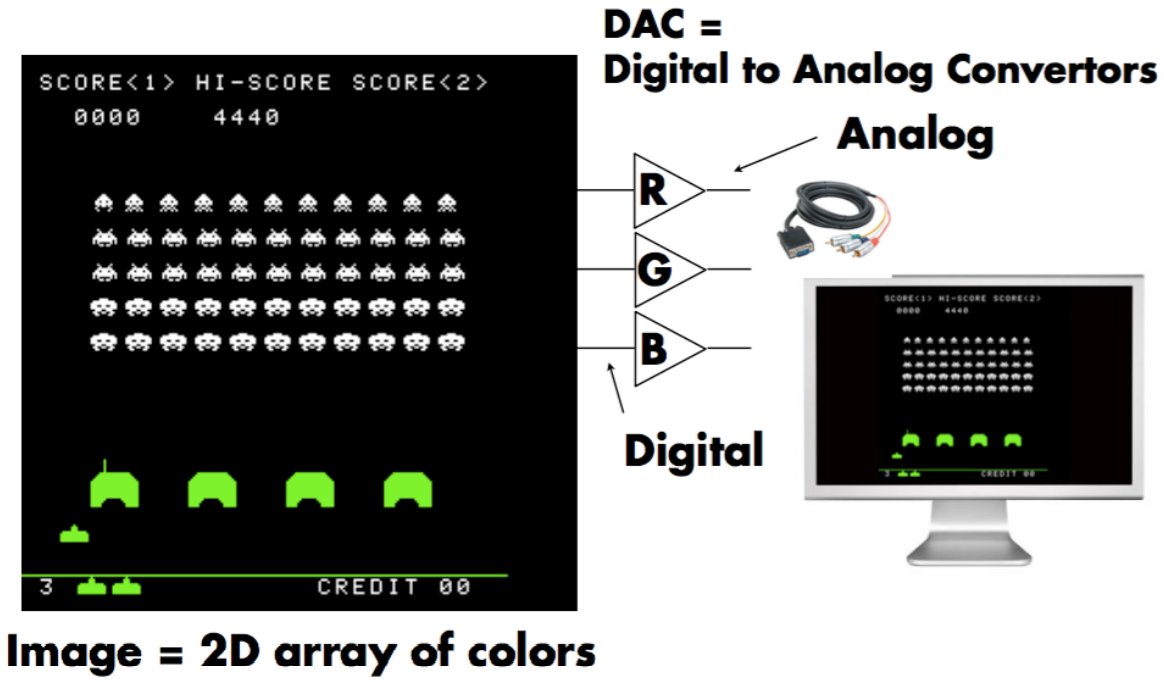
平板显示设备 LCD,OLED等:计算器,手机等
- LCD(Liquid Crystal Display,液晶显示器):液晶通过自己的不同排布,影响光的偏振方向
- 光经过竖直的光栅后是不能再通过水平光栅的,但液晶可以通过排布,将光扭曲成水平的,进而通过水平光栅
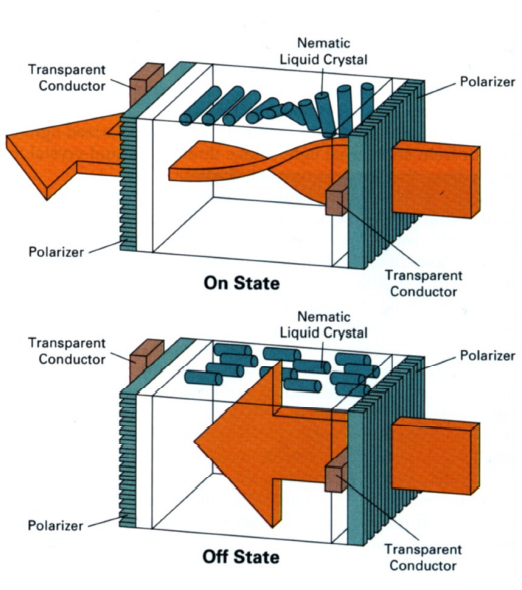
LED(Light emitting diode,发光二极管)
Electrophoretic 电子墨水屏:Kindle
- 经过不同电压,可以把黑白墨水进行排布,刷新率低
三角形
为什么是三角形
- △是最基础的图形,可以表示复杂的图形
- 有一些独特的性质
- 一定在一个平面上
- 有清晰定义的内、外部,可以用叉乘判断点是否在三角形内部(之前讲的)
- 定义三角形的三个顶点后,内部可以通过任意点跟顶点的位置关系,得到渐变的关系
- 用于中心坐标的插值方法
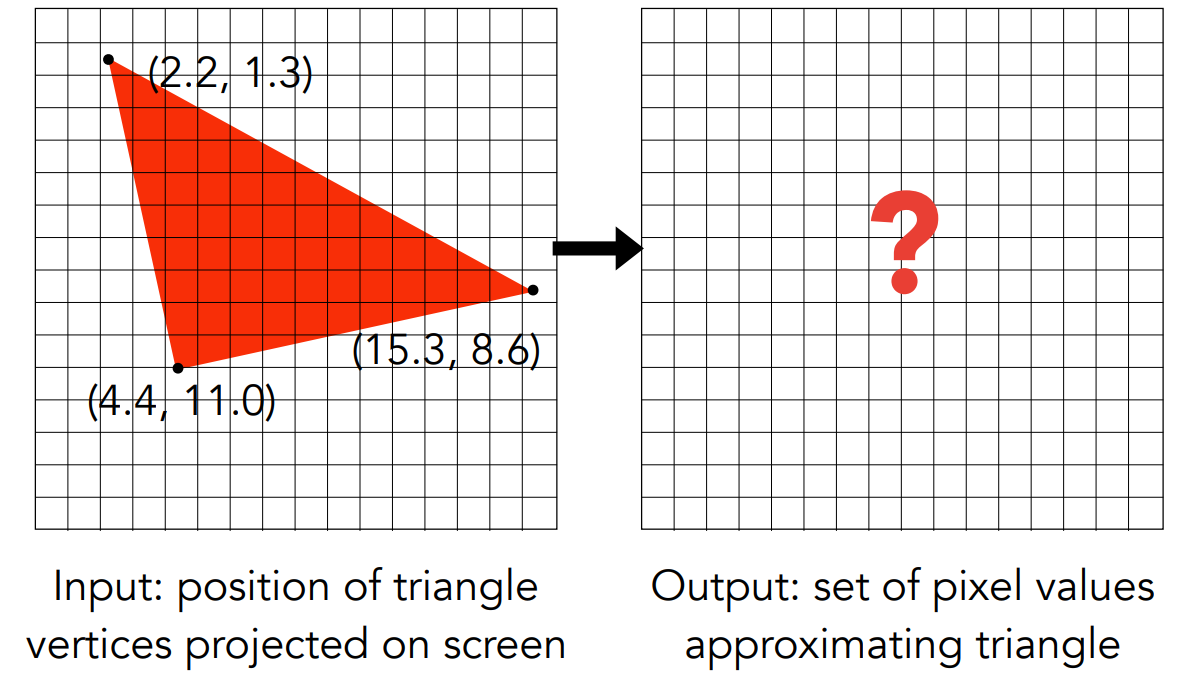
通过前几步MVP变换、视口变换,物体的 $x,y$ 都投影到了屏幕空间中,每个3D中的三角形,都可以在屏幕中找到它的3个顶点。怎样把三角形变为像素?
判断像素和三角形的位置关系
像素是正方形。考虑像素的中心点跟三角形的位置关系
一个简单的光栅化方法:Sampling(采样)
采样的概念
- 给定一个连续的函数,在不同的地方,问函数的值是多少
- 采样就是把一个函数离散化的过程
for(int x=0;x<xmax;++x) output[x] = f(x);- 此处,利用像素的中心,对屏幕空间进行采样
- 采样是图形学的重要概念。还会对 time(1D),area(2D),direction(2D),volume(3D) 进行采样
采样方法
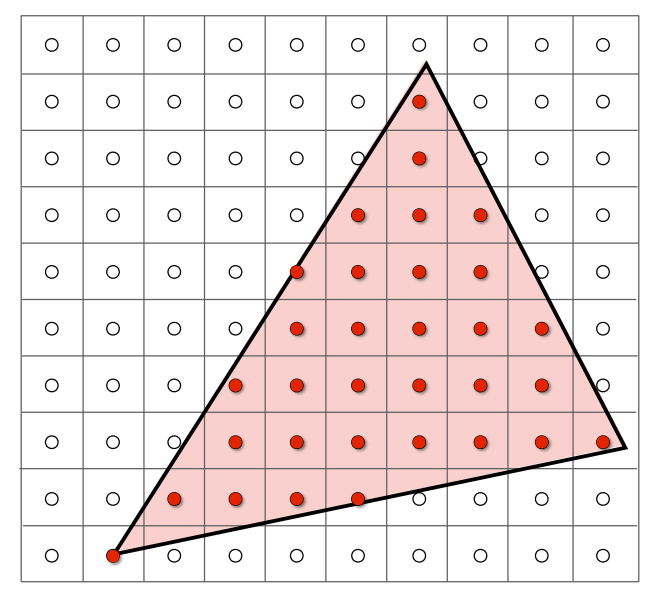
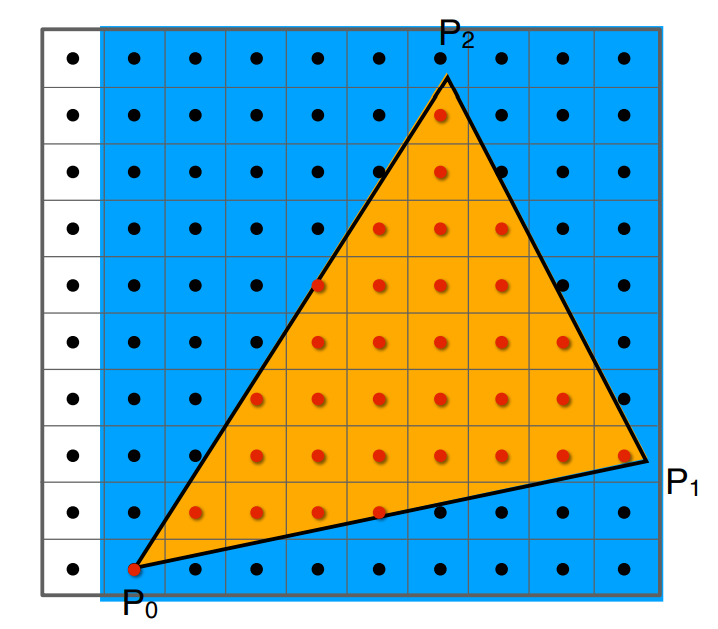
定义一个函数 inside(t, x, y),判断像素 $(x,y)$ 的中心 $(x+0.5,y+0.5)$ 是否在三角形 $t$ 内
for(int x=0;x<xmax;++x)
for(int y=0;y<ymax;++y)
image[x][y] = inside(tri, x+0.5, y+0.5);使用向量叉乘的方法实现 inside(t, x, y)
- 把三角形安排成某种顺序,比如△ABC,循环成ABCABC,找到 $\vec {AB},\vec{BC},\vec{CA}$
- 跟 $\vec {AP},\vec{BP},\vec{CP}$ 叉乘,如果结果全是正向量或全是负向量,说明点 $P$ 在△ABC内部
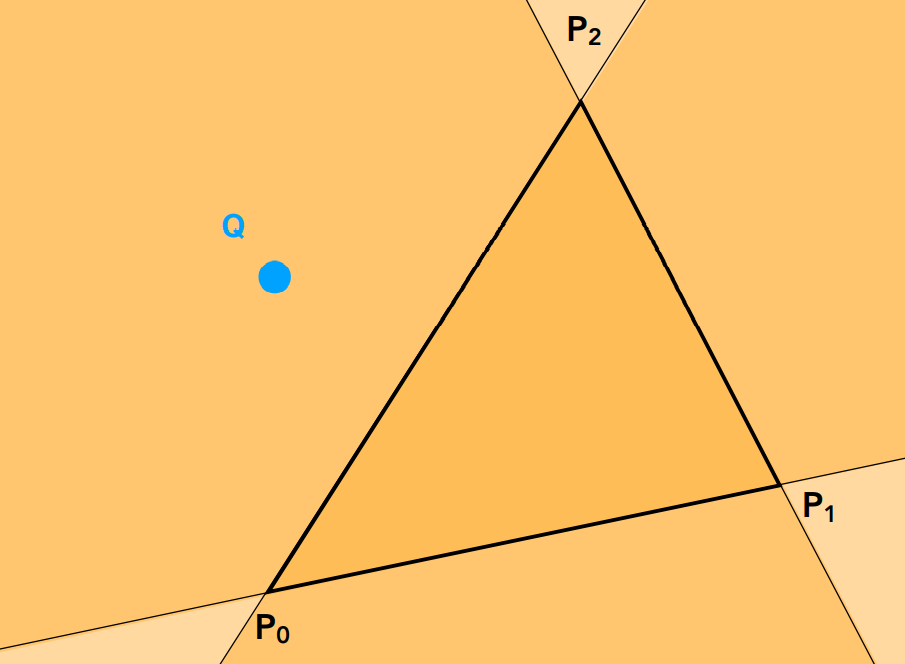
如果点正好在三角形的边界上怎么办?
- 比如边上的点是否属于三角形;两个三角形交界处的点,是都属于还是都不属于,还是属于一边
- 对于图形学遇到的 Edge Cases,要么不做处理,要么特殊处理
- 对于本课,不做处理
- 在OpenGL,规定上、左边算在内部,下、右边不算
对于一个三角形,只检查它 Bounding Box 范围内的像素
一个简单方法是取轴向包围盒AABB,即对三个点取 $x,y$ 的最大、最小值
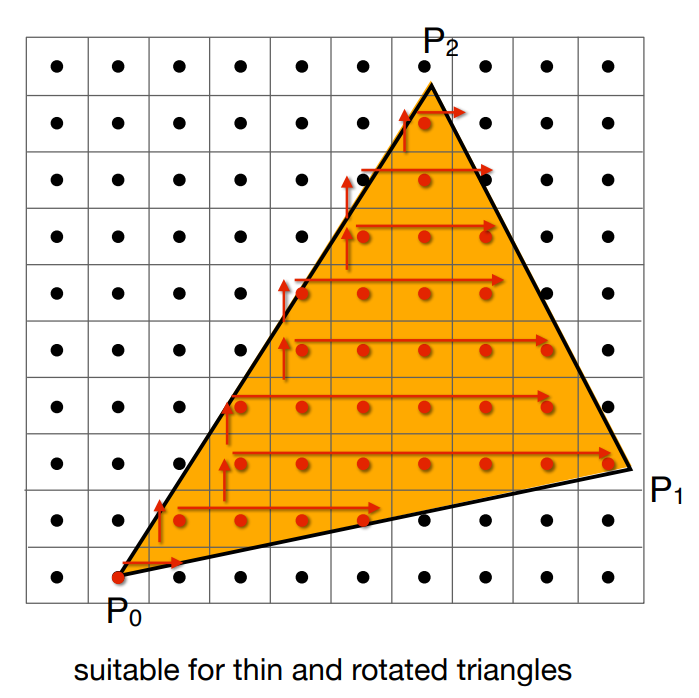
还有方法对于每行找最左和最右,不多考虑任何一个像素
- 适合于又细又斜的三角形,AABB很大
实际的光栅化
理论上,光栅化就是:对于每个可能的像素,检测其是否位于三角形内部
实际上屏幕的光栅化
手机
iPhone的一个像素分为红绿蓝三个条;Galaxy的一个像素是 bayer pattern,绿色点更多(因为人眼对绿色更敏感)

打印机
- 减色系统,cmyk

在本课中,依然认为:每个像素的内部,是一个颜色均匀的小方块
一个小问题
光栅化图形学中,有一个严重问题:锯齿 Jaggies
产生的原因:像素本身有一定大小,并且像素的采样率对于信号是不够高的,产生了信号的走样问题
带来了抗锯齿/反走样技术

(为什么通过采样的概念来分析这个问题?)
Lecture 06 - Rasterization 2 (Anti-aliasing and Z-Buffering)
Rasterization
Viewing
- View / Camera + Projection(Orthographic, Perspective) + Viewport
Rasterizing triangles
- Point-in-triangle test
- Aliasing
Antialiasing
- Sampling theory
- Antialiasing in practice
Visibility / Occlusion
- Z-buffering
1 - 信号处理概念简述
1.1 采样和 Aliasing
概念
采样是计算机图形学的常用方法,在时域、空间概念上都会用到。可以理解视频为每帧进行一次采样,然后排列起来。
Sampling Artifacts 概念为:在图形学中,一切看上去不对的结果。
由采样引起的 Artifacts,称为 “Aliasing”:
- Jaggies,空间中采样出现的锯齿问题
- Moire Pattern,摩尔纹,对图片下采样
- Wagon wheel effect,时间中采样,人眼的采样率跟不上物体的运动速度,导致看到相反的旋转方向
Aliasing Artifacts 问题的成因:
- 信号变化得太快,而采样速度太慢
抗锯齿 / 反走样技术
根据之前的步骤,视口变换将 $[-1,1]^3$ 的物体画在屏幕空间中;然后进行光栅化,对可能在三角形内的像素中心点进行采样。在采样后,出现了 Jaggies(锯齿),这个问题叫做 Aliasing。
针对这个问题,使用抗锯齿 / 反走样技术。
一种技术:采样之前做模糊(低通滤波),然后再做采样
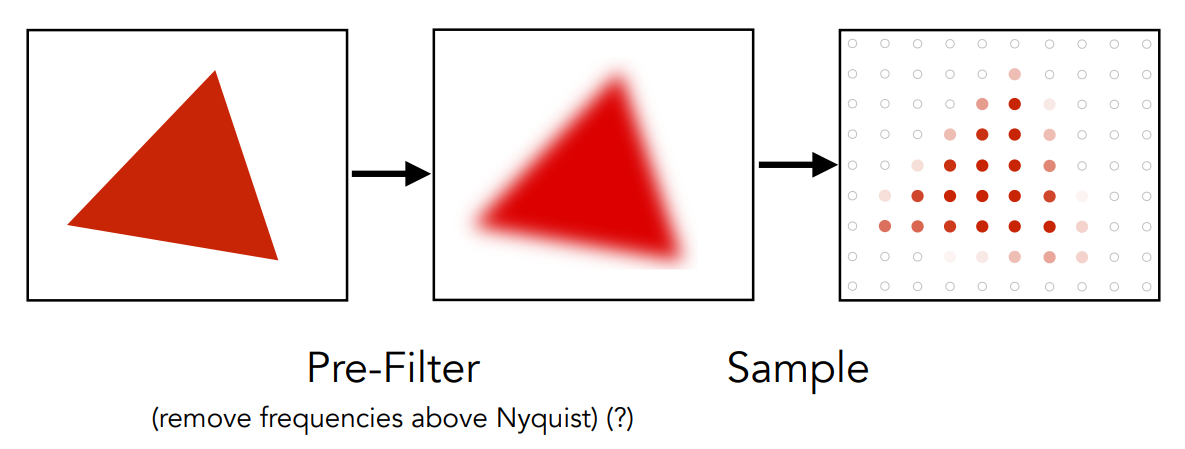
- 先模糊、再采样的方法称为 Blurred Aliasing
- 如果反过来,先采样、再模糊,达不到期望的效果

更本质上的问题:
- 为什么采样速度跟不上信号变化的速度,就会产生走样?
- 为什么先采样、再模糊,达不到反走样的效果?
对这些问题进行分析,需要频域方面的知识
1.2 傅里叶变换,频域和时域
频域(Frequency Domain)
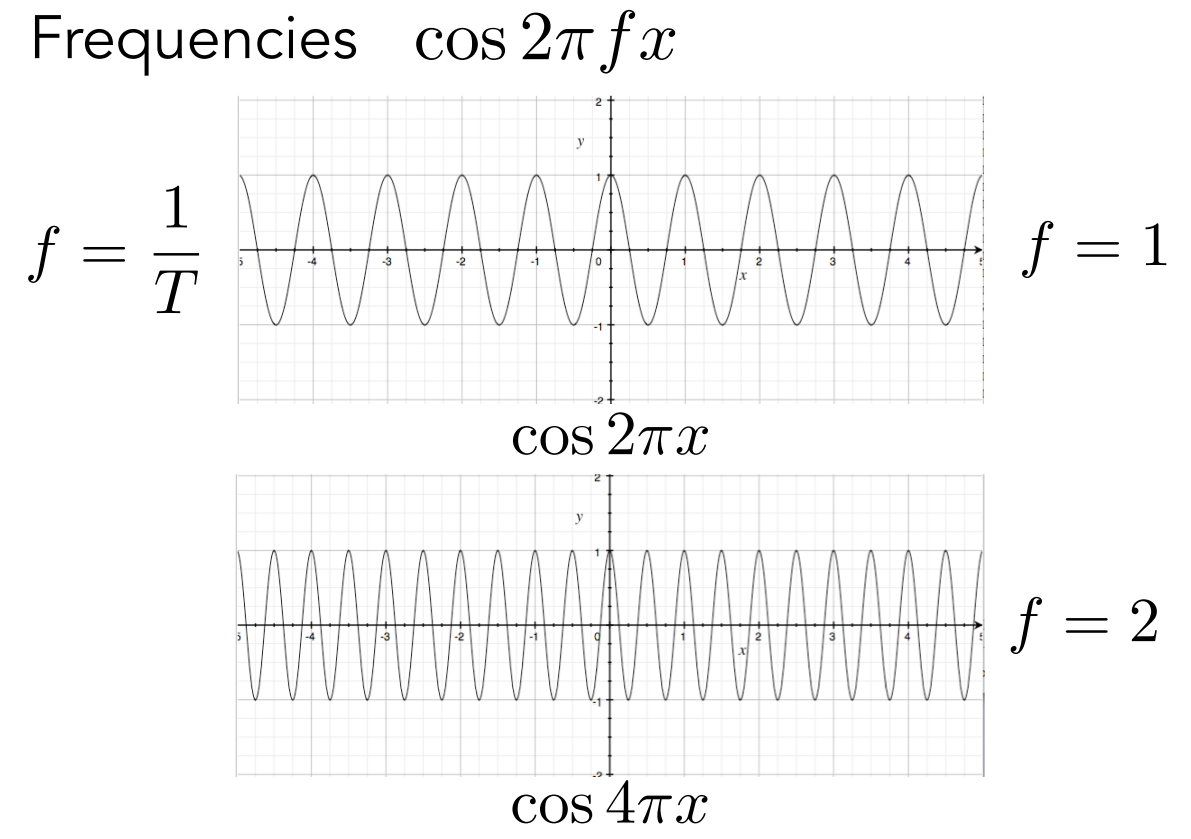
- 通过正弦、余弦波函数的系数 $f$,可以定义函数的频率、周期
- 在微积分中,可以对一个函数进行傅里叶级数展开
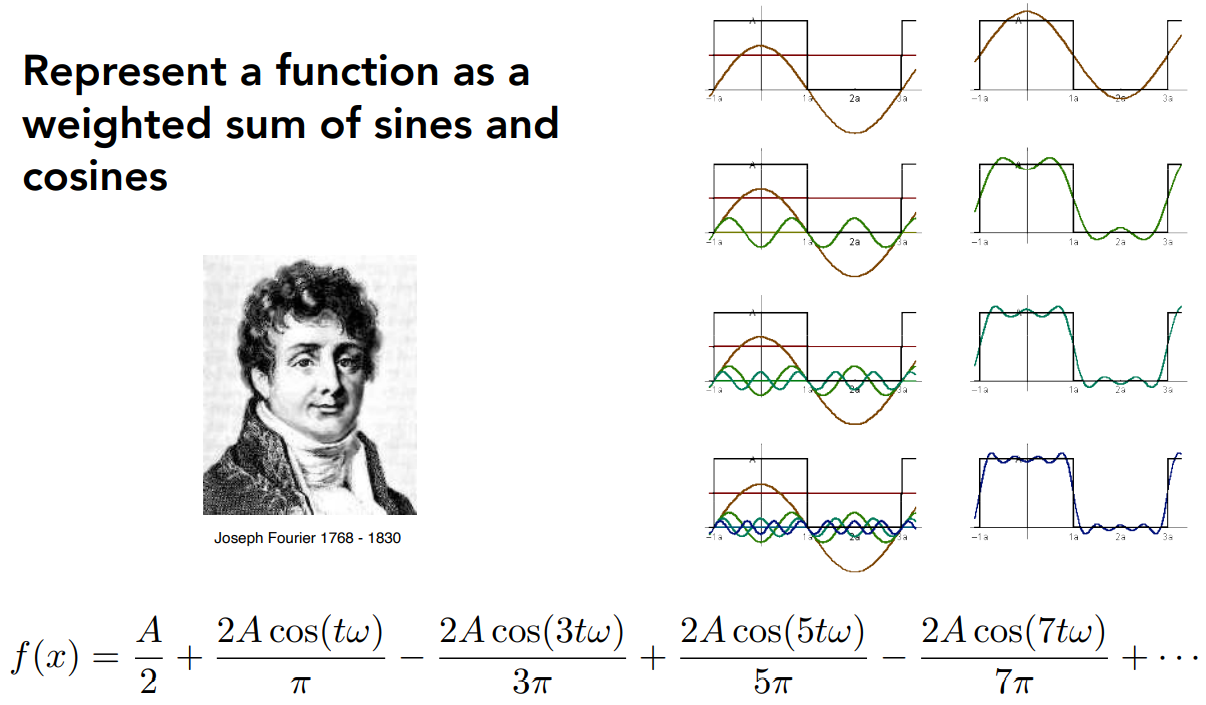
- 任何一个周期函数,都可以写成一系列正弦、余弦函数的线性组合,以及一个常数项
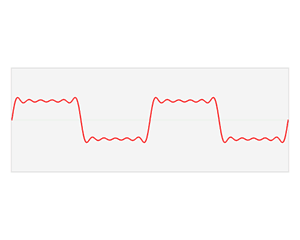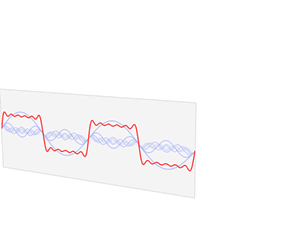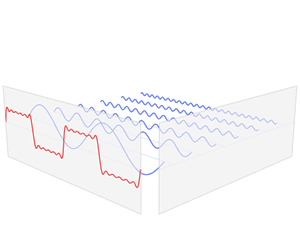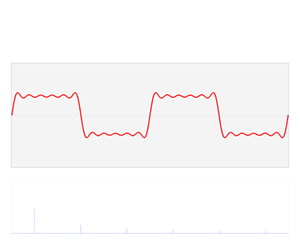
- 图中展示了一个像城墙一样的函数的拟合过程,从上到下函数依次加入4个正/余弦函数项,左边是各个函数的图像,右边是加起来的拟合结果
- 傅里叶级数展开跟傅里叶变换的概念是相似的
- 一个函数可以通过复杂的变化,转变成另一个函数,并且能通过逆变换再转换回来
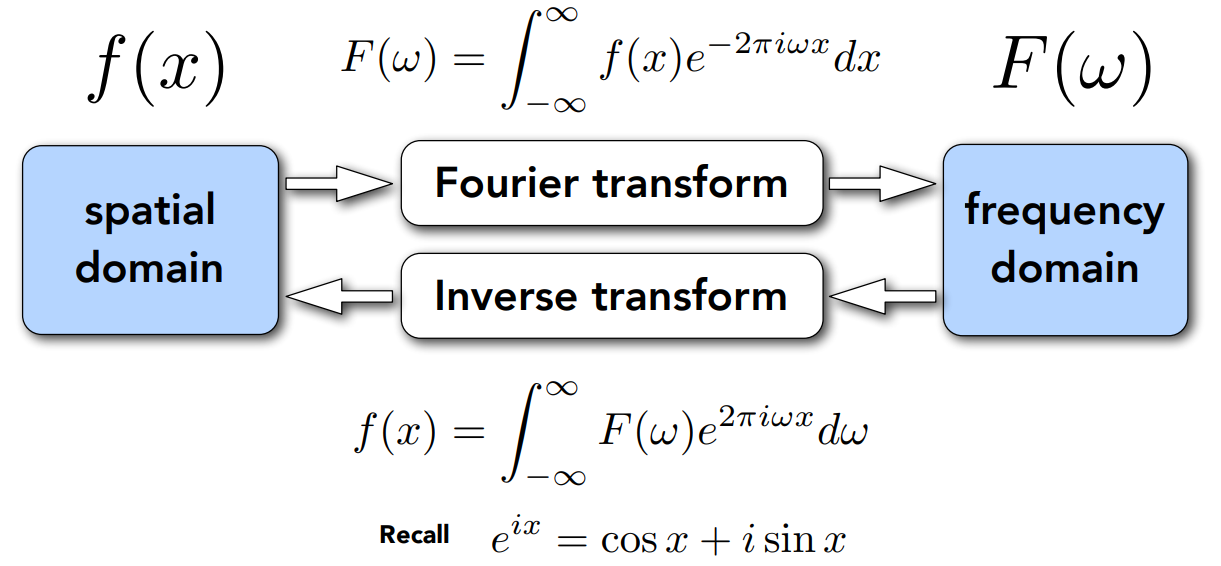
- 通过傅里叶级数展开,可以发现,任何一个函数都可以分解成不同的频率函数的线性组合,具体来说是不同频率从低到高的组合
- 由此,傅里叶变换是把函数变成不同频率的段,并把不同频率的段显示出来
- 采样频率和函数频率
- 从上到下,频率越来越高的五个函数,对于每个函数进行相同频率采样点的采样
- 发现:频率越高,越无法通过采样,将函数“恢复”,这就代表函数丢失了一部分高频信息
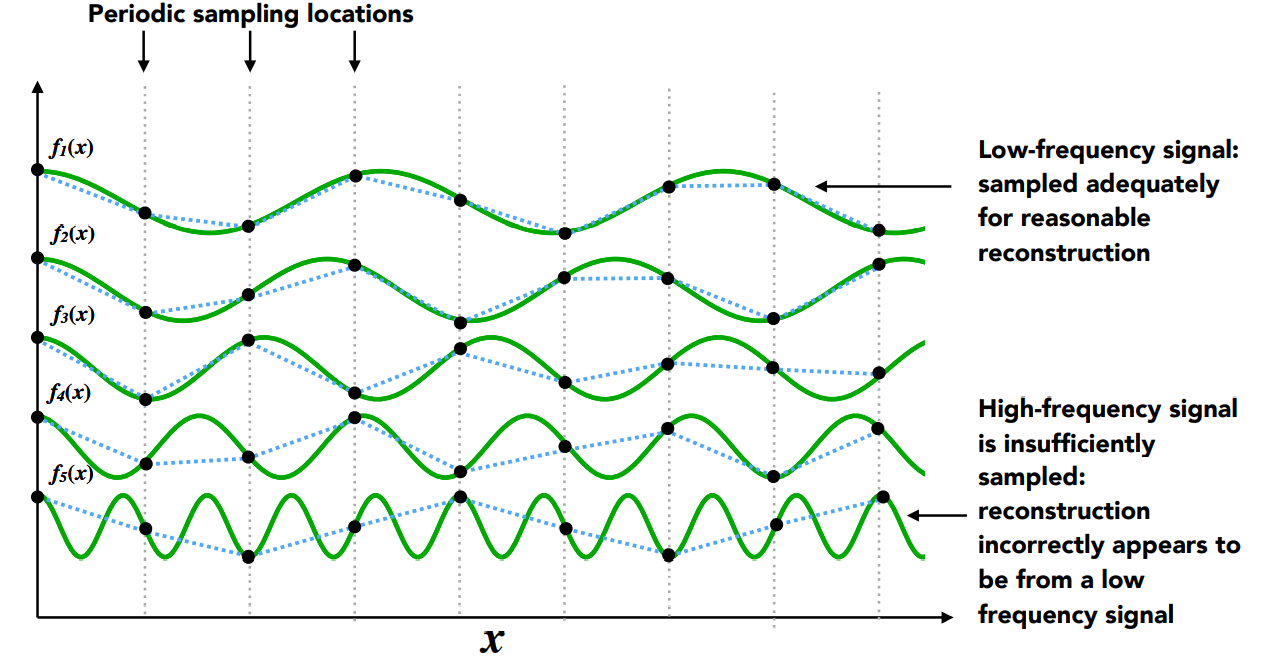
- 采样频率跟不上函数变换频率,就不能通过采样,将函数的信息恢复出来
- 此外可以发现,使用同样的采样率,采样不同的函数(如下图蓝、黑两个函数),会得到完全一致的采样结果
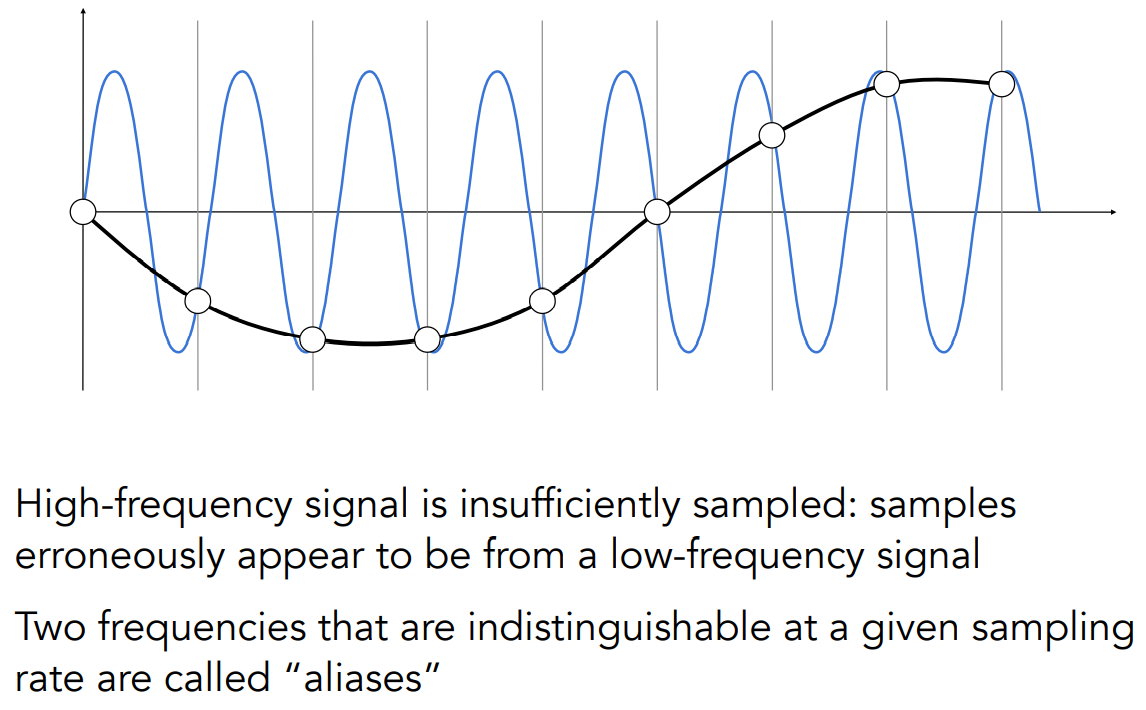
- 用同样的采样方法采样不同的函数,得出的结果无法区分,这就是走样 / 混叠(aliases)的概念
- 补充:时域和频域的理解
- 傅里叶变换把函数的时域和频域联系起来
- 关于时域和频域,可以参考这一个问题下的回答
1.3 滤波,卷积,平均
滤波,高频和低频
Filtering(滤波):把特定频段的频率删掉
傅里叶变换可以把函数从时域变到频域。傅里叶变换让我们看到任何信号(包括图像)在各个不同的频率是什么样子,称为频谱。
频谱图:

- 频谱图中间的频率低,周围的频率高
- 对于大多数图片,信息都集中在低频
- 由于图片本身不是周期性重复的信号,就认为它是水平、竖直堆叠复制的,在两张图边界部分会产生极其高的高频,因此出现了右图水平、竖直两条线。对于图片内部的分析,可以忽略这两条线
高通滤波:
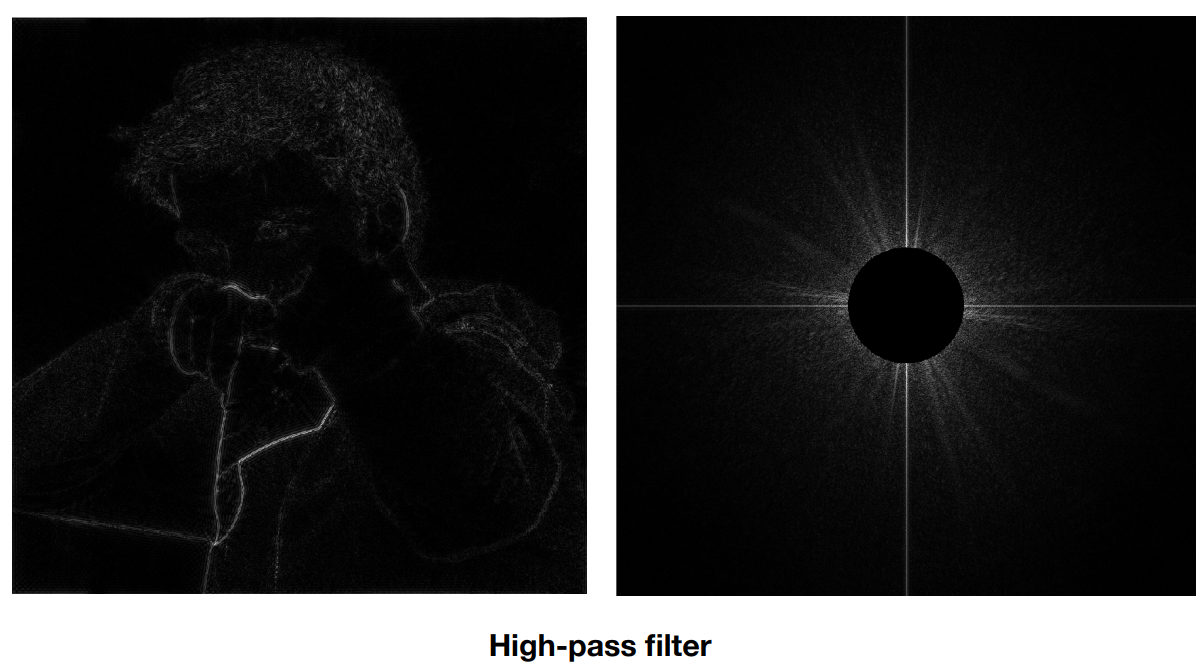
- 把低频过滤掉,只留高频,再进行逆傅里叶变换,发现原图像留下了内容上的边缘(理解为原图边界处发生剧烈的变化,信号蕴含高频的信息)
- 称为高通滤波
低通滤波:

- 反过来留下低频、过滤高频,称为低通滤波,也就是舍弃了图片变化大的部分(比如边界)
- 逆傅里叶变换的图像的意义是进行了模糊处理,整个图片的变化减小
- 逆傅里叶变换的图像有些水波纹,这是不完美的低通滤波产生的问题
某一频段滤波:
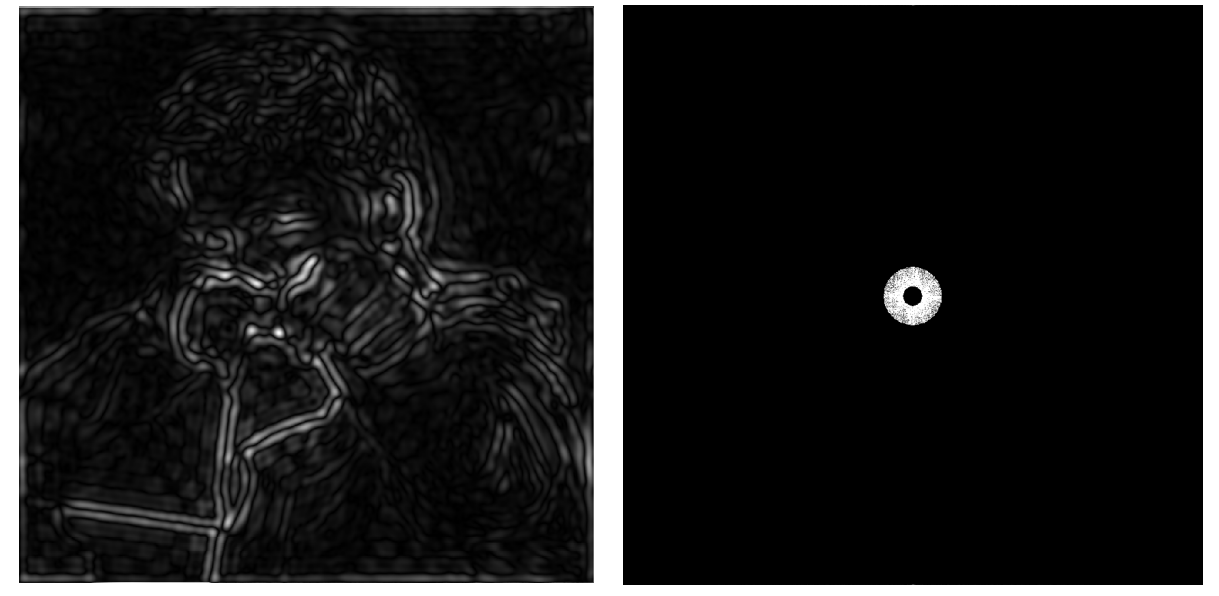
- 去掉高频、也去掉低频,留下某一频段的信息,对应原图剩下了不是很明显的边界特征
- 去掉了最外面的边界(对应高频信息)、去掉了内部的色块(对应低频信息)
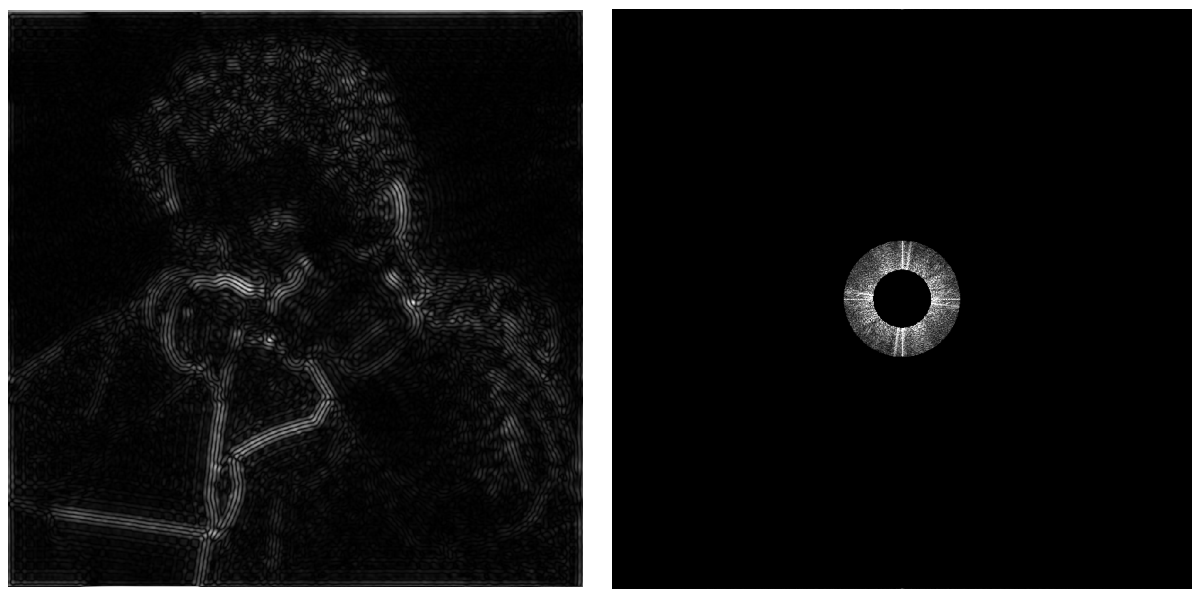
- 对于上一步,留下更高频的信息,对应到图片上也更接近高频的边界
这是数字图像处理的内容,最近对于图像的处理已经更多使用深度学习技术,而不直接做频率上的变化了
Filtering滤波 = Convolution卷积( = Averaging平均)
- 平均
- 低通滤波对应图像模糊,也就是图像像素上的“平均”操作
- 卷积
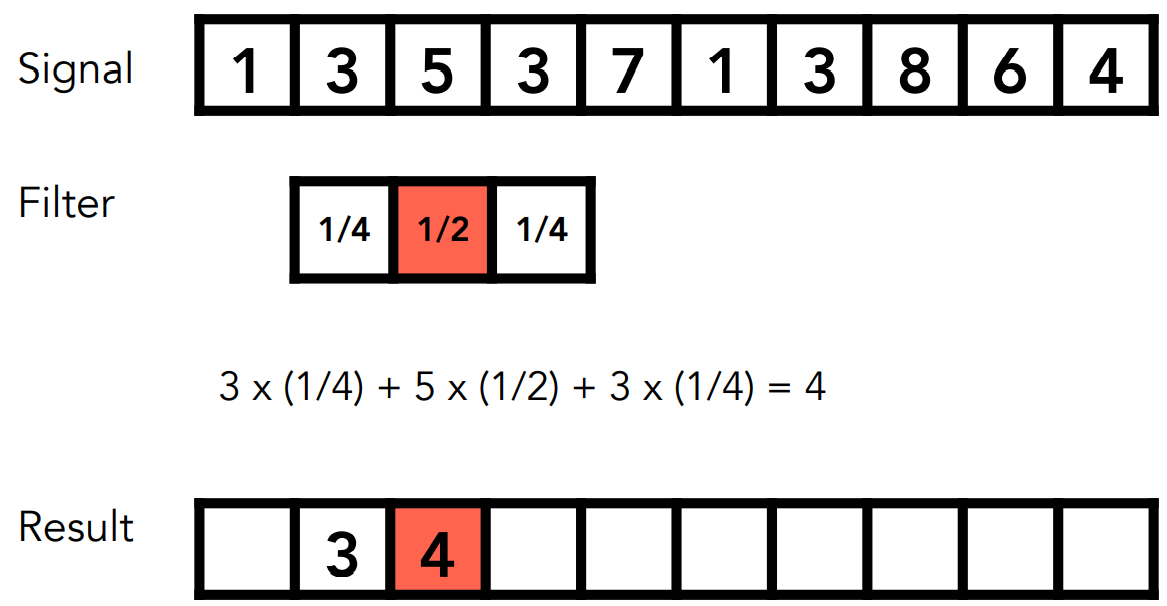
- 把窗口在信号上移动,窗口的权重跟窗口覆盖的信号值进行点乘
- 卷积得到的是:信号每个位置在周围的加权“平均”
- 卷积定理
- 时域上,对两个信号做卷积,对应到两个信号各自的频域上,是各自频域上的乘积(时域的卷积是频域的乘积)
- 在时域上的乘积,意味着是在频域上的卷积
- 卷积操作
- 对于一张图,可以直接用卷积的滤波器(卷积核),对图进行卷积操作
- 也可以用傅里叶变换,将图变到频域上,再把卷积滤波器变到频域上,把两者相乘得到频域的结果;再做逆傅里叶变换,变回时域上的图像
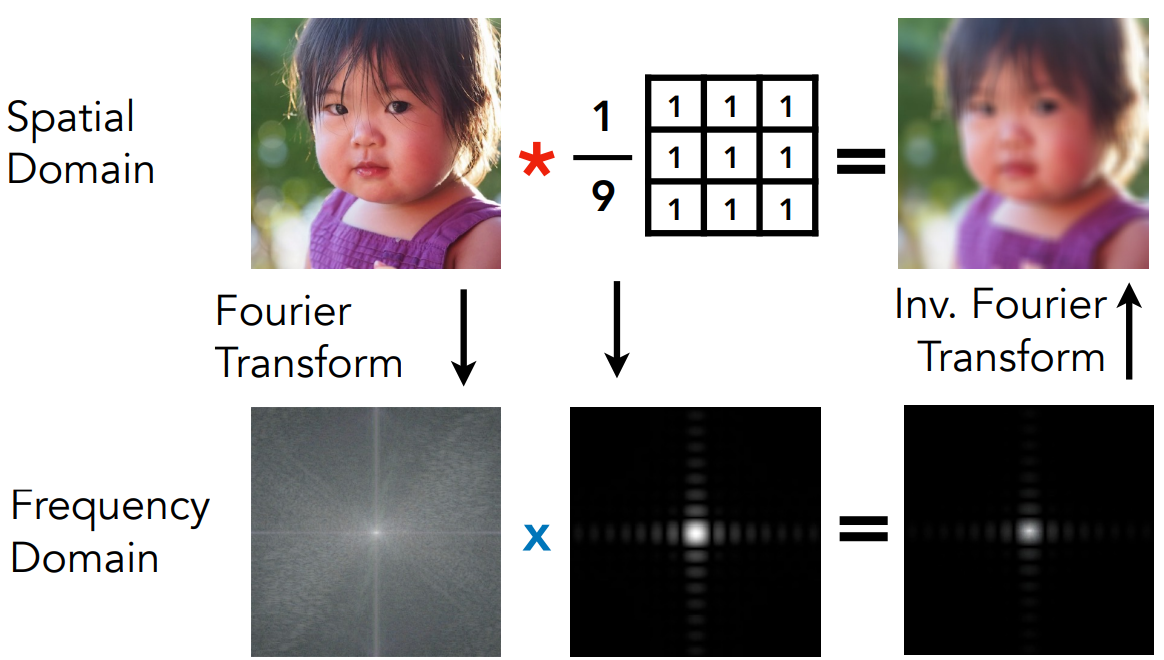
- 如图,可以直接使用卷积核,对图做卷积
- 也可以把图、卷积核都做傅里叶变换到频域上,然后在频域上把两个频谱相乘,得到的结果再逆傅里叶变换成图
- 时域上,对两个信号做卷积,对应到两个信号各自的频域上,是各自频域上的乘积(时域的卷积是频域的乘积)
- 卷积核
- 上图中,卷积核的元素都是1,它的作用是:不改变颜色,但对于 $3\times3$ 范围内做平均。观察卷积结果,发现图像被模糊
- 在频域上可以看出,这个滤波器基本上是低通滤波(保留频域图中间的低频部分)。跟图片相乘,只留下图片的低频信息
- 说明:卷积 = 低通滤波 = 平均
- box filter也称为低通滤波器
- 如果用更大的box,像素的取平均范围变大,对应更模糊的图像,也就是更低频率的低通滤波
- 也就是,box越大,对应的频域图像越小

1.4 回到采样和 Aliasing
Sampling 采样 = 重复频域上的内容
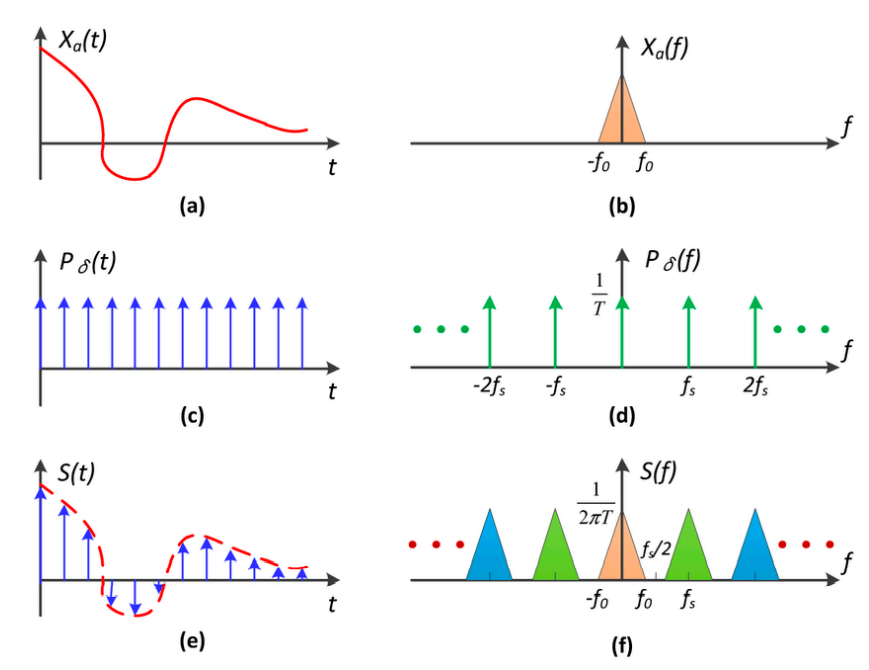
- 左边都是时域,右边都是频域
- (a) 的傅里叶变换结果是 (b)
- (c) 冲激函数的定义是,只在某一些位置上有值
- (d) 是经过傅里叶变换的冲激函数,依然有冲激函数的性质
- 用 (c) 乘以 (a) 函数,会得到一个个离散的点,也就是 (e),这就是采样的过程
- 时域上:给定一个原始信号 (a),乘上冲激函数 (c),得到采样的结果
- 把 (b) 和 (d) 进行卷积,同样得到频域上的采样结果 (f)
- 时域上的卷积相当于频域上的乘积
- 频域上:给定一个原始频域 (b),跟冲激函数的频域 (d) 做卷积,得到采样的结果
- 发现:时域上 (e) 作为采样的结果,频域上 (f) 其实是原始的频谱 (b) 复制粘贴了很多份
- 采样就是在重复一个原始信号的频谱
Aliasing 走样
- 为什么会产生走样现象?
- 采样就是在重复一个原始信号的频谱,以不同频率采样,就对应不同间隔(步长)的重复。
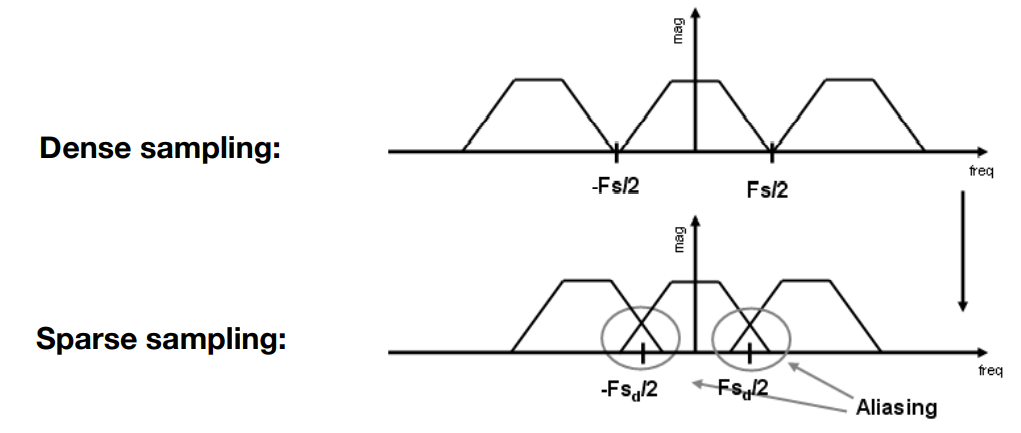
- 图中是频域上的复制关系,时域上采样率高,也就是周期小,到了频域上 $f$ 更大,也就是搬移间隔大
- 采样率低时,搬移的间隔小,频谱的复制密集,叠在了一起
- 这种情况叫 走样 / 混叠 Aliasing
2 - 反走样方法 antialiasing
理论解决思路
- 从根本上解决:增加采样率
- 增加屏幕的分辨率,像素小、采样率高,频谱的搬移间隔大,不容易出现混叠
- antialiasing方法
- 先做模糊,再做采样
- 模糊:低通滤波,去掉高频信息,让频谱覆盖的范围小一些
- 采样:频谱范围变小,不容易发生混叠
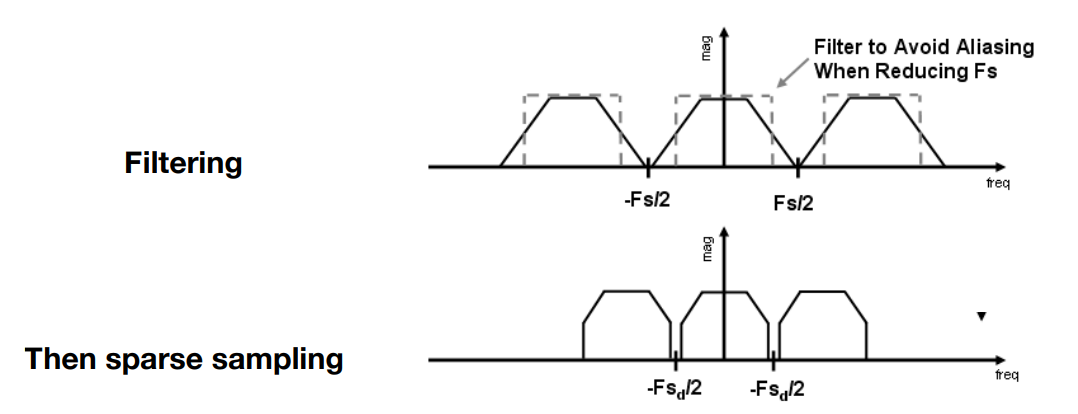
- 实际操作中,怎样进行模糊操作?
- 用一定大小的低通滤波器进行卷积即可。前面提到,box filter就是低通滤波器
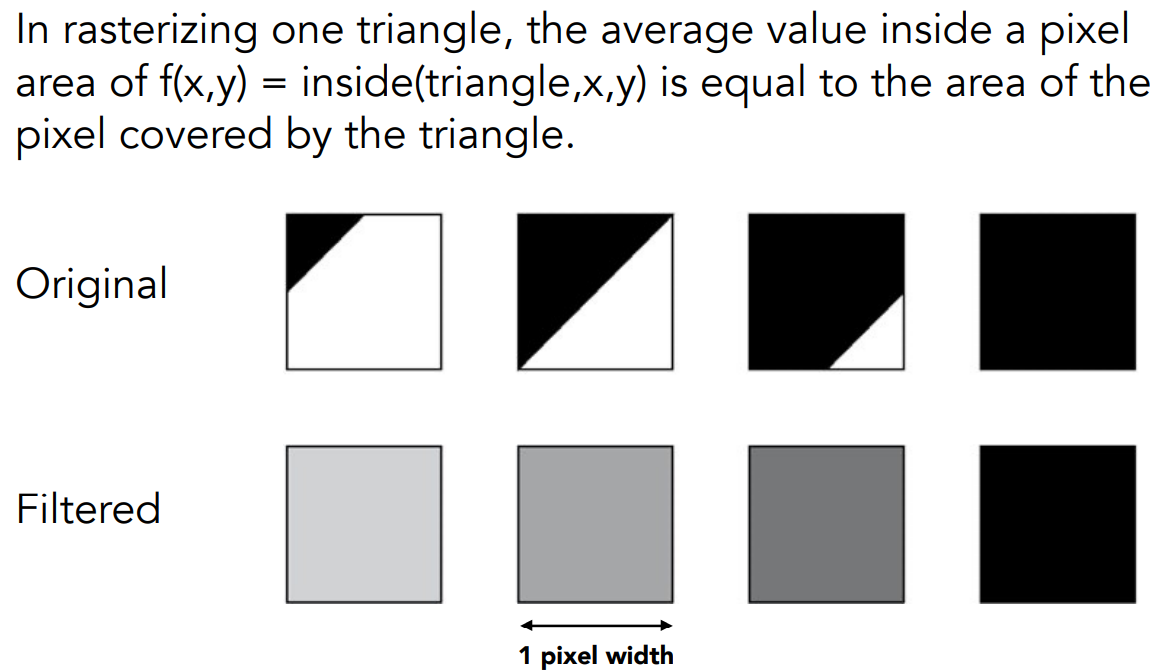
- 具体来说,使用 1-pixel box filter,对于每个像素,计算它的平均值(因为光栅化后,像素可能被覆盖一部分,1-pixel box filter可以求出像素的平均颜色)

- 先做模糊,再做采样
实际方法
理论上,对于每个像素求覆盖的区域,然后取平均,但很难实现
近似方法:MultiSampling Anti-Aliasing(MSAA,多重采样抗锯齿)
认为一个像素划分为很多小的像素
- 对于每个小像素的中心,判断其是否在图形内
- 然后把每个像素中的所有小像素计算结果取平均,作为整个像素的结果

如图使用 $2\times2$ ,一像素有 3 个小像素位于三角形内,则认为该像素的值是 75%
注意:MSAA实际只对应抗锯齿中的模糊操作,并没有采样。MSAA只是近似得出一个合理的覆盖率,并不是提高了分辨率,而直接解决 aliasing 问题。
其他
NFL定律中,MSAA带来的cost是什么?
增大计算量
工业界并不是完全如同 $4\times4$ 做像素的划分,而是按更合理的图案分割,有些点还可以被临近不同的像素复用
因此,采用 $4\times4$ 的抗锯齿,不会直接让帧率变小 4 倍
其他的抗锯齿方案
- FXAA(Fast Approximate AA,快速近似抗锯齿):
- 不增加样本数,而是是一个图像的后处理
- 得到有锯齿的图 -> 把锯齿边界找到 -> 换成没有锯齿的边界
- TAA(Temporal AA,时间抗锯齿)
- 复用上一帧像素的信息
- 相当于把MSAA对应的样本分布在时间上,对于运动的物体在之后实时光线追踪再说(因为实时光线追踪核心思想跟TAA一样)
- FXAA(Fast Approximate AA,快速近似抗锯齿):
超分辨率 Super resolution / Super sampling
- 把小分辨率的图转换成高分辨率的图,同时不看到锯齿
- 跟MSAA都是解决采样样本不足(采样率不够)的问题,本质相同
- 一种解决方法:DLSS(Deep Learning Super Sampling)
总结
aliasing现象出现的原因是信号变换得太快,而采样率太慢。为了解决这个问题,要么提高采样率(用更高分辨率、划分出更多像素),要么使用“先做模糊再采样”的antialiasing方法。
傅里叶变换建立了时域到频域的联系,我们得知:时域上的卷积相当于频域上的乘积。
而对于采样,我们用冲激函数跟带采样函数相乘,在频域上得知:采样其实是搬移一个信号的频谱。采样率低,对应时域上周期长、频域上搬移间隔(频率)小,容易在频域上发生混叠。
通过卷积=低通滤波=平均的操作,让图片变得模糊,可以过滤掉高频的信息。也就是让频域更窄,搬移后不容易混叠。
而先采样、再模糊就不能做到antialiasing了,因为采样后的信号发生混叠,模糊只会去掉混叠后的大信号的高频信息。
对于光栅化中的锯齿问题,针对每个像素,先模糊(把像素内部对应的图形进行模糊),再采样(这个模糊后的值作为像素的值)。比如MSAA方法,把每个像素划分成小像素,分别计算小像素是否在三角形内部,然后计算大像素在三角形内的比例(模糊)作为采样结果(采样)。
3 - 深度测试 Z-buffering
可见性和遮挡问题
把一个三角形画在屏幕上,需要先进行光栅化,划分成像素格子;然后对像素中心进行采样,查看它是否在三角形内;为了解决反走样,往往使用先做模糊、再采样的方式。
场景中的三角形离相机的距离各不相同,会产生 Visibility / Occlusion 可见性和遮挡问题。
在画家算法(Painter’s Algorithm)中,体现在每个三角形的渲染顺序上
- 把所有的三角形进行深度排序,按照从远到近的顺序绘制所有三角形,也就从远到近完成整幅画
- 适用于三角形进行深度排序的场景。n个三角形时,复杂度是 O(nlogn)
- 有不能解决的情况:
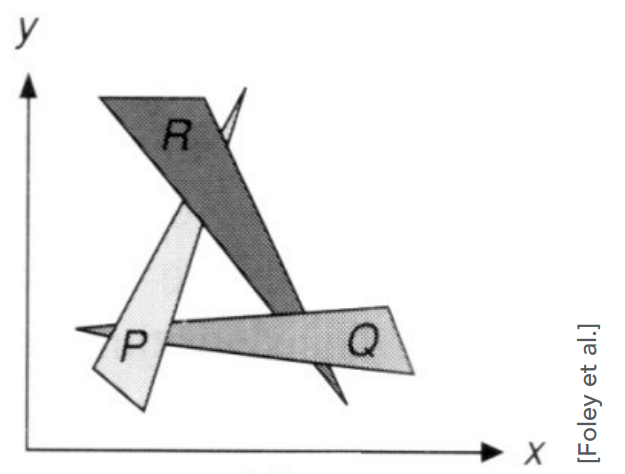
- 无法定义深度顺序,就不能应用画家算法
图形学中,使用 Z-buffering(深度缓存)解决这个问题
- 不好对每个三角形进行深度的排序,但可以对每个像素记录像素表示的几何的最近距离
- 同时渲染两张图
- frame buffer,存储颜色值,相当于最后的渲染结果
- depth buffer(z-buffer),存能看到物体的最浅深度,利用这个信息维护遮挡关系

- 在之前,规定相机放在原点、朝 $-z$ 方向看,因此越近的物体深度值越大。在此处为了简化计算,认为:相机看到的深度理解为相机到物体的距离,永远是正的。小的 $z$ 值表示深度小、离得近
- 查看上图的右边depth buffer,离相机越近,深度值越小,颜色越黑;离相机越远,深度值越大,颜色越白
- 绘制过程:对于一个像素,刚开始画了地板,就把地板对应的深度记下来;后面放上了物体,物体上的三角形覆盖了这个像素,物体在像素上的深度比地板更小,因此该像素在左图 frame buffer 绘制物体、在右图 z-buffer 记录物体的深度
Z-Buffer Algorithm
初始化 depth buffer 为 ∞
在每个三角形光栅化过程中:
for(each triangle T) // rasterization
for(each sample(x, y, z) in T) // sampling 已经光栅化到屏幕上了,(x,y)是在屏幕上的坐标
if(z < zbuffer[x, y]) // closest sample so far
framebuffer[x, y] = rgb; // update color
zbuffer[x, y] = z; // update depth
else ; // do nothing, this sample is occluded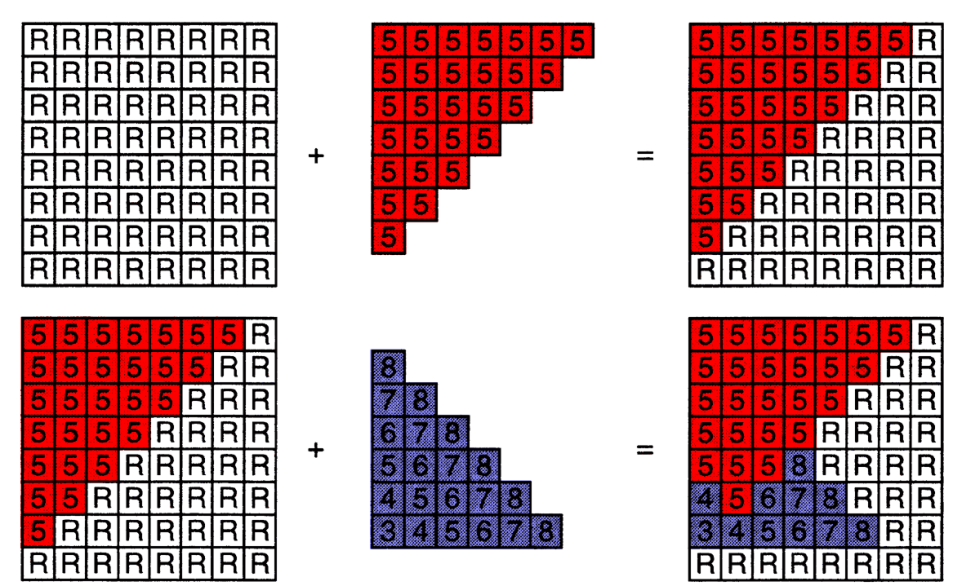
n个三角形、分别覆盖常数个像素个数,复杂度是 c*O(n)
- 只是对每个像素记录了最小深度,并没有实际上排序
深度缓存的一个性质:跟三角形的绘画顺序是没有关系的
- 此处假设两个物体的某个像素的深度值永远不相等,因为运算得来的浮点数基本上不可能相等
- 在实际场景中确实会出现深度相等的情况,此处先不提
深度缓存算法是目前被广泛采用的算法,被用在各种GPU硬件中
- 为了反走样,采用MSAA算法,对于每个像素取很多个采样点,Z-Buffer会对每个采样点进行深度的记录
Z-Buffer处理不了透明物体的深度。对透明物体需要特殊处理
Lecture 07 - Shading 1 (Illumination, Shading and Graphics Pipeline)
目前以完成的步骤:
- model transformation,生成一个3D世界,得到图1
- 进行Camera/View transformation,摄像机移到原点,物体也跟着移动,得到图2
- 进行Projection transformation(orthographic,perspective),物体投影到 $[1-,1]^3$ 的立方体空间中
- 进行Viewport transformation,舍弃z轴信息,物体进入2D屏幕,得到图3
- Rasterization(sampling,Antialiasing,Z-Buffer),得到图4
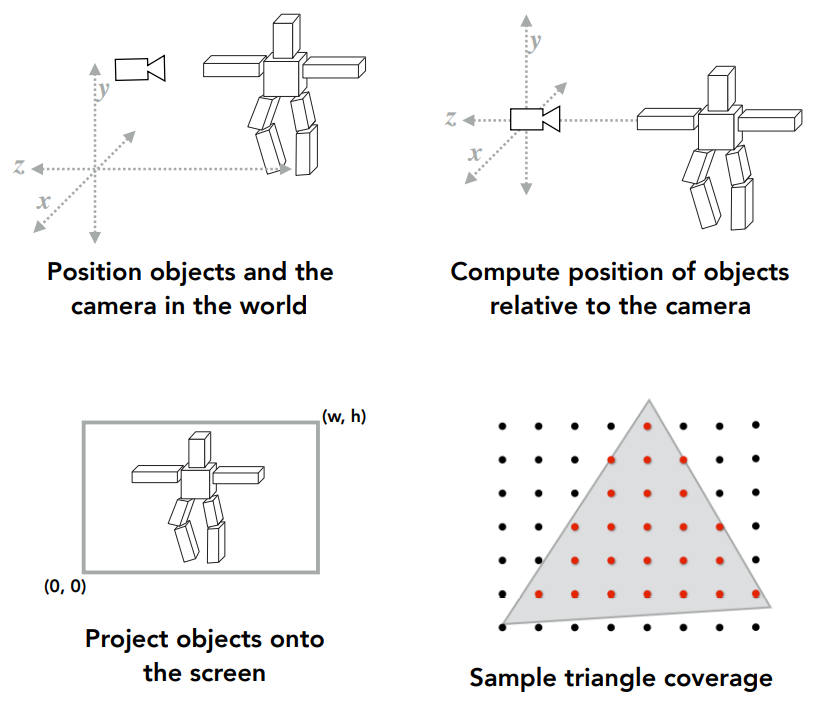
到此,不同三角形被画在屏幕上,填充对应的像素。这些像素的颜色应该是什么?(Shading)
1 - Shading
Shading基础
定义
- shading的本意:绘画中不同的明暗和颜色。(The darkening or coloring of an illustration or diagram with parallel lines or a block of color.)
- 对于本课:shading 是对于不同物体,应用不同材质的过程
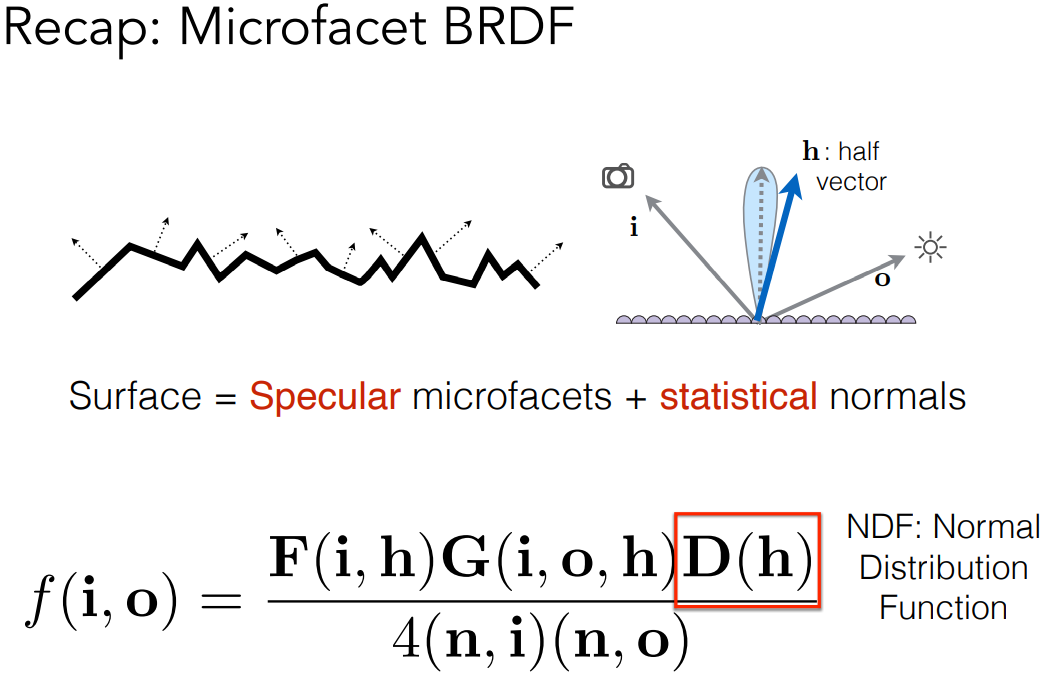
一个简单的着色模型:Blinn-Phong 反射模型
- Specular highlights:高光,表面很光滑,光线向镜面反射方向附近反射
- Diffuse reflection:漫反射,表面不光滑,光线被反射到四面八方
- Ambient lighting:间接光照,不直接接触光,接受环境的反射光

2 - Blinn-Phong 反射模型
Blinn-Phong 反射模型总览
目的
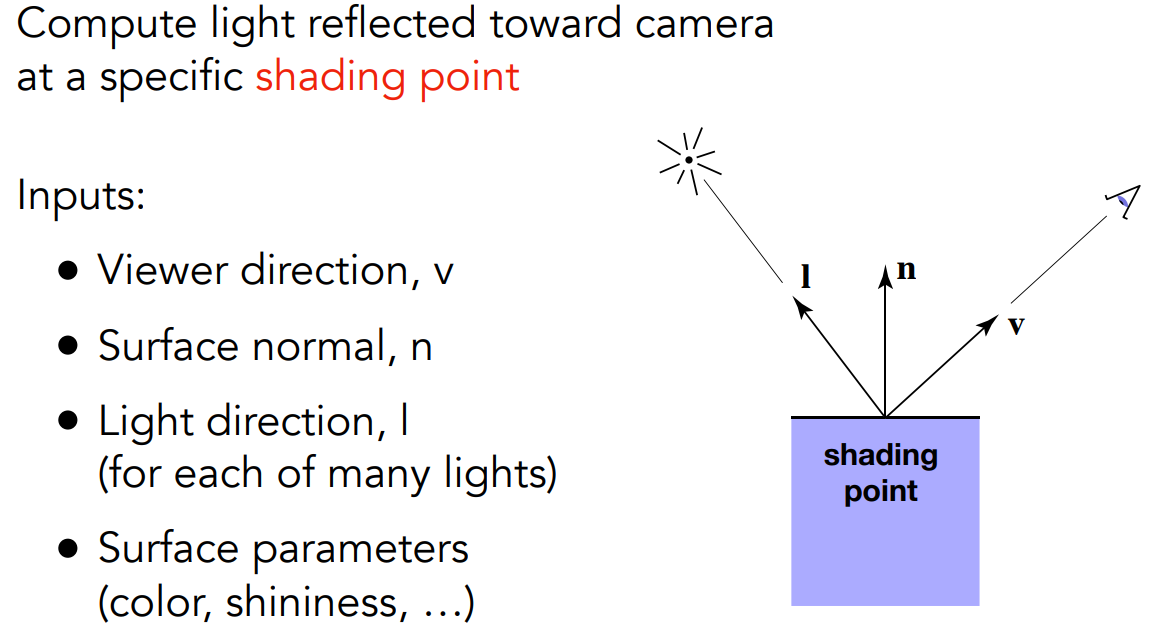
- 考虑任何一个点(shading point)上的着色结果
- shading point 位于一个物体表面上,在小范围内是一个平面
- Blinn-Phong 模型给定 shading point 的一些属性。根据这些属性,有的点会发生漫反射,有的点发生镜面反射。模型最终求的是这个点的光照情况
- 从光源到 shading point,光的能量可能会衰减,但求得该点接收的能量后,就不考虑从该点到观测点的能量传递过程了
定义量
- 定义一些方向
- 定义一个法线方向 $\vec n$
- 定义观测方向是从 shading point 指向相机的方向,$\vec v$
- 定义光照方向是从 shading point 指向光源的方向,$\vec l$
- (只定义方向,以上都是单位向量)
- 物体表面相关的属性
- 有多亮(shininess,跟亮度不同),颜色等
- shading ≠ shadow
- Shading is Local,考虑一个点的着色情况,就只考虑它自己和几个方向;不考虑其他物体的存在
- 只考虑 shading point 点和其他几个方向,不考虑这个点是否在阴影内
- 可以看到图中物体接收左上方的光照,有了明暗的变化,但体现不出来阴影

Blinn-Phong 模型之 Diffuse Reflection(漫反射)
概念
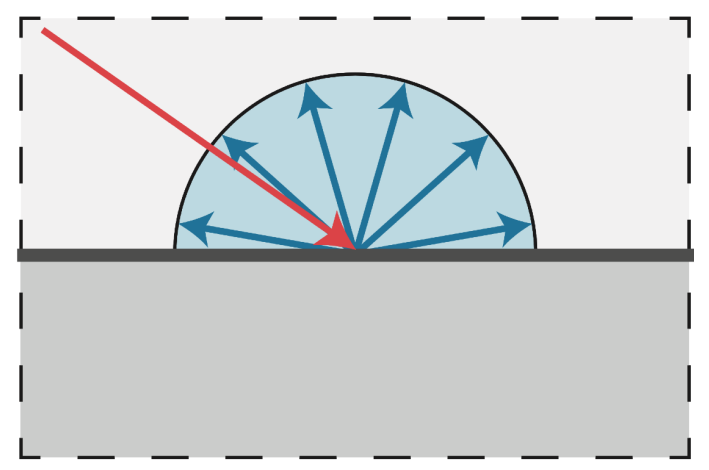
- 漫反射:光线打到物体的某个点时,光线被均匀地反射到各个方向去
- 光的接收
- 当物体表面的朝向和光照方向有一定的夹角,得到的明暗是不一样的
- 考虑光是一种能量,看到的物体的明暗相当于物体接收到了多少能量
- 考虑 shading point 周围单位面积内接收到了多少能量
- 理解为四季的变换,南北半球接收太阳直射的能量不同,体现为冬季和夏季
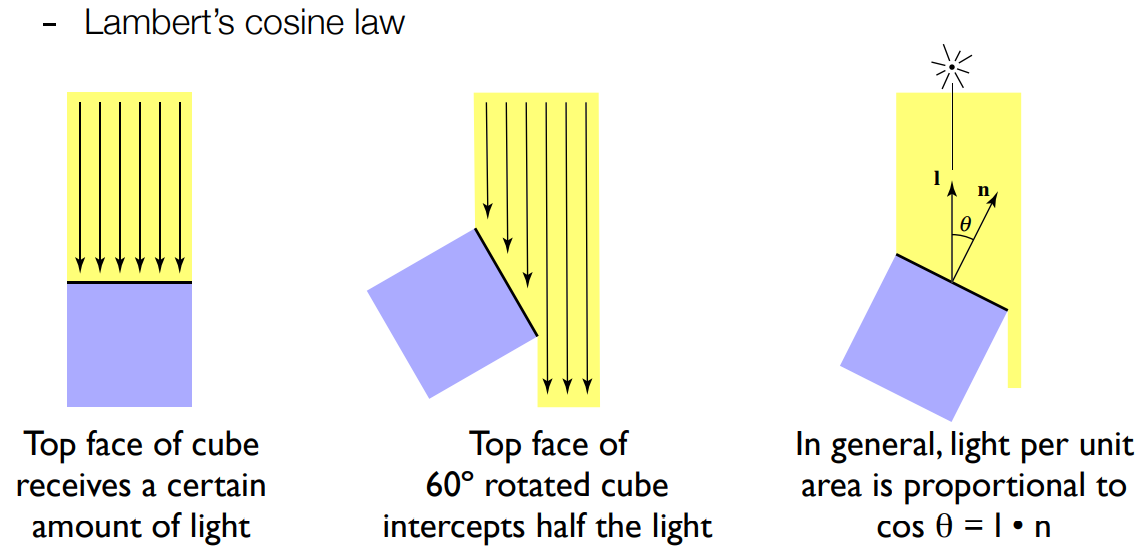
- Lambert’s 余弦定理:接收到的能量跟光照方向、法线方向夹角的余弦呈正比
- 光照方向跟法线方向接近垂直,光是平行打向表面的,shading point 上接收不到多少能量
- 光照方向跟法线方向相同,光垂直打向表面,shading point 接收到最多的能量
- 光的发散
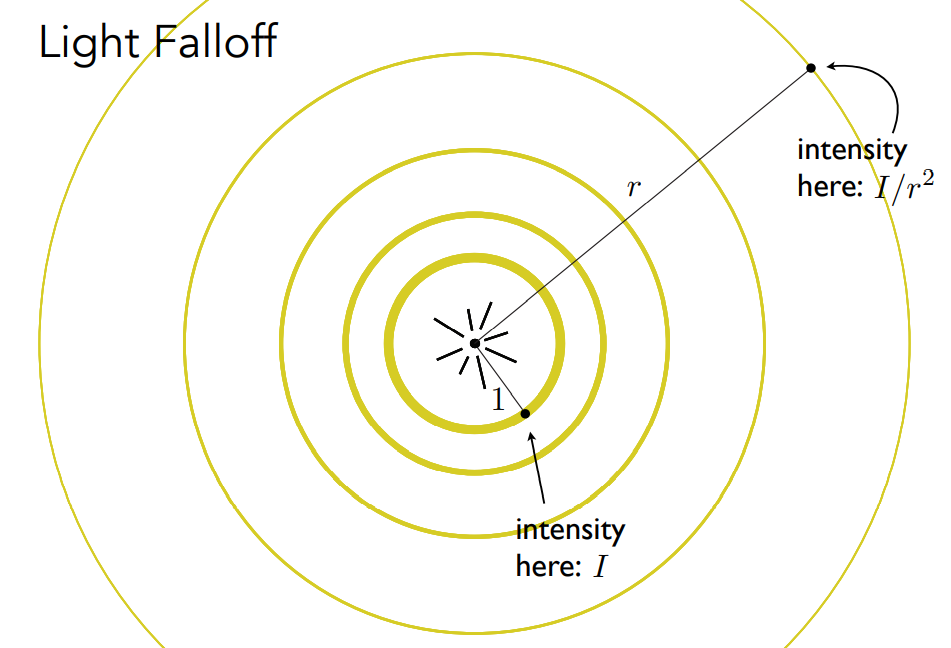
- 认为点光源产生了光,无时无刻不在向四面八方辐射能量
- 观测方法:考虑某个时刻发出的所有能量。在任何一个时刻,点光源辐射出的能量集中在一个球壳上;在下一个时刻,光集中在更外面的球壳上
- 能量是守恒的,近的球壳和远的球壳具有相同的总能量
- 小的球壳上,每一个点的能量更多
- 传播过程中,球壳表面积变大,每一个点对应的能量越少
- 暂时定义一个强度 $I$,对于距离为 $1$ 的球壳,总能量 $4\pi I$;对于距离为 $r$ 的球壳,$4\pi r^2 I’= 4\pi I$,$I’=I/r^2$
- 光线在传播过程中,单位面积在任何位置能接收到的能量(也就是强度 $I$),跟光线的传播距离的平方呈反比
计算
$L_d = k_d \frac{I}{r^2}\max(0, \bold {n\cdot l})$
- 结合起来
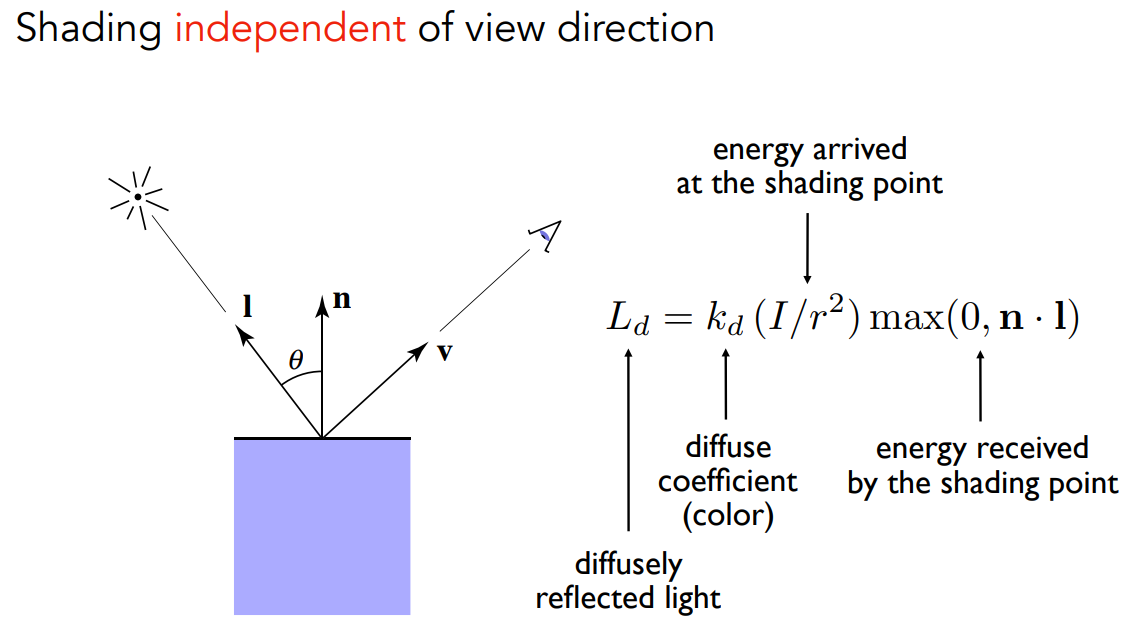
- 由 Light Falloff,如果知道一个点光源,并且知道 shading point 离点光源的距离,就可以知道有多少光传播到了点光源附近
- 由 Lambert’s cosine law,可以知道这些光如何在 shading point 上被吸收
- $L_d = k_d (I/r^2)\max(0, \bold {n\cdot l})$
- $r$:shading point 到光源的距离;$I$:单位面积上的光能量;$I/r^2$:到达 shading point 处的光能量
- $\bold {n\cdot l}$:两个单位向量的点乘(也就是余弦),如果得出负数就取 0,物理意义上只考虑反射、不考虑从下方照来的光的折射
- $(I/r^2)\max(0, \bold {n\cdot l})$ :接收了多少能量(到达该点的总能量,减去被吸收的能量,剩下的就是能发射出去的能量,也就是吸收了多少能量)
- $k_d$:点的反射率。点本身有明暗,点吸收一部分能量、反射另一部分。如果把这个量定义成R/G/B三个通道上的明暗,也就定义了这个点的颜色
- 最终得出 $L_d$:对于一个发生漫反射的点,最终我们能看到多少能量,也就是这个点的明暗
- 由于漫反射出来的能量均匀打到各个方向,不管从哪个方向观察它,都得到相同的能量,看到一模一样的结果。漫反射跟观测方向 $\vec v$ 完全无关
- 漫反射的结果
- 可以看出,光源位于左上方
- 同一个石膏球,右下方法线方向跟光照方向接近垂直或反向,余弦值小,反射的能量少,看起来暗
- 不同的石膏球,对于不同的反射率 $k_d$,反射率越高,反射的能量越多,看起来越亮

Blinn-Phong 模型之 Specular Term(高光)
概念和计算
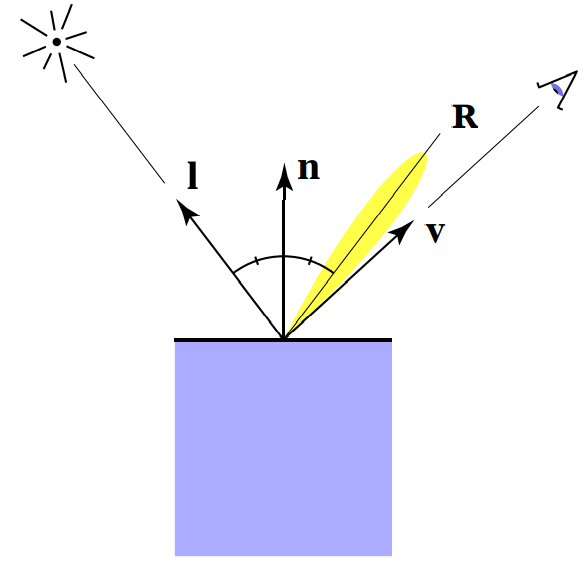
高光说明物体比较光滑,光线反射的方向接近镜面反射的方向。由于观察的方向 $\bold v$ 跟镜面反射方向 $\bold R$ 接近,因此能看到高光。
Blinn-Phong 模型做出一个假设:观察方向 $\bold v$ 跟镜面反射方向 $\bold R$ 接近,就是法线方向 $\bold n$ 跟半程向量 $\bold h$ 接近
- 半程向量:两个向量的角平分线方向,这些向量都是单位向量
- $\bold h = \text{bisector}(\bold v, \bold l)\frac{\bold v+ \bold l}{||\bold v+ \bold l||}$
- 通过向量点乘判断接近,单位向量接近则点乘结果接近1
- 这样就不需要计算反射方向 $\bold R$ 了。计算 $\bold R$ 跟 $\bold v$ 是否接近的模型是 Phong 模型,Blinn-Phong 模型在此处做了计算上的简化,因为计算 $\bold h$ 比计算 $\bold R$ 简单
$L_s=k_s(I/r^2)\text{max}(0, cos\alpha)^p=k_s(I/r^2)\text{max}(0, \bold n\cdot\bold h)^p$
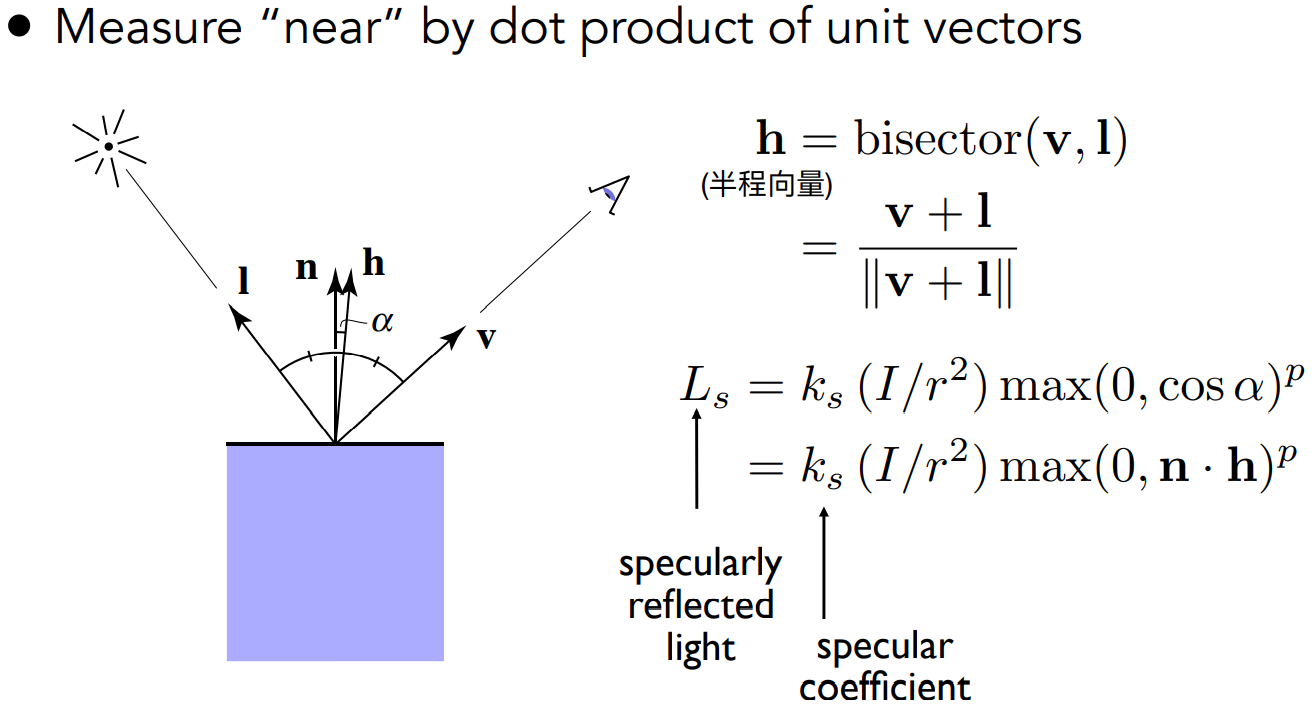
- $k_s$ 是镜面反射系数
- 通常认为镜面反射都是白色,$k_s$ 就是白色
- $(I/r^2)$
- 跟漫反射一样,$(I/r^2)$ 考虑多少能量到达 shading point
- 但比起漫反射,不再考虑多少能量被吸收,也就是考虑入射角度跟平面的夹角。此处没考虑,是因为 blinn-phong 作为经验模型,把这一点简化了
- 我的理解,可以是因为平面很光滑,能量基本上都被反射了,没有被吸收。只考虑观测方向能否保证我们看到高光
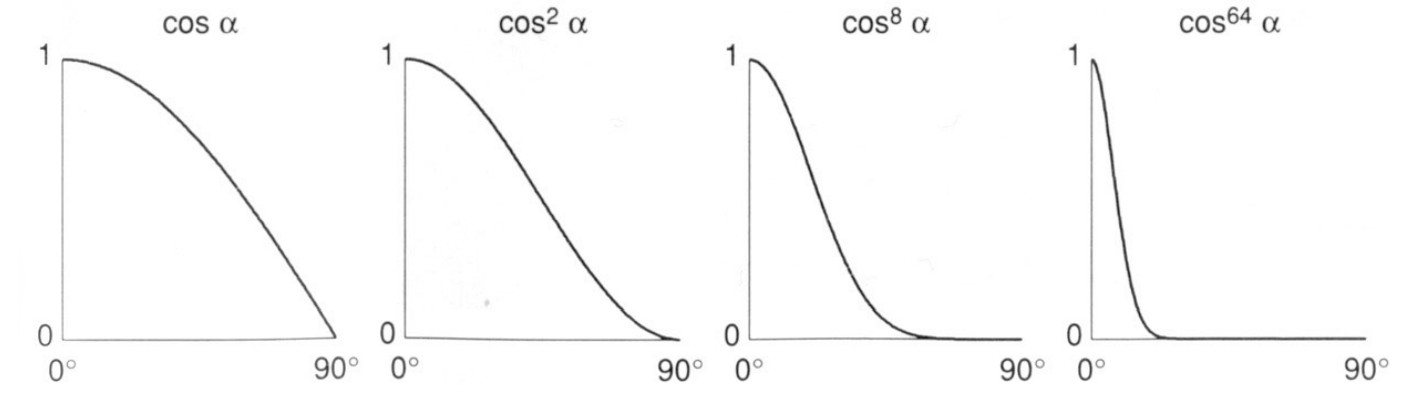
- $\text{max}(0, \bold n\cdot\bold h)^p$
- $\text{max}(0, \bold n\cdot\bold h)$ 间接衡量观察方向跟反射方向的的接近程度,用半程向量更好算
- $p$ 次方提高夹角余弦的衰减程度,达到角度差一点、就看不到高光的效果。可以控制看到高光的大小。$p$ 通常取 $[100,200]$
漫反射+高光的结果

- 对于每一列,镜面反射系数 $k_s$ 增大,表示它的亮度
- 对于每一行,从左到右 $p$ 增大,偏转角度越来越严格、高光越来越小
Blinn-Phong 模型之 Ambient Term(环境光)
概念和计算
- Blinn-Phong 模型认为任何一个点接收来自环境中的光永远都是相同的,强度为 $I_a$、来自四面八方
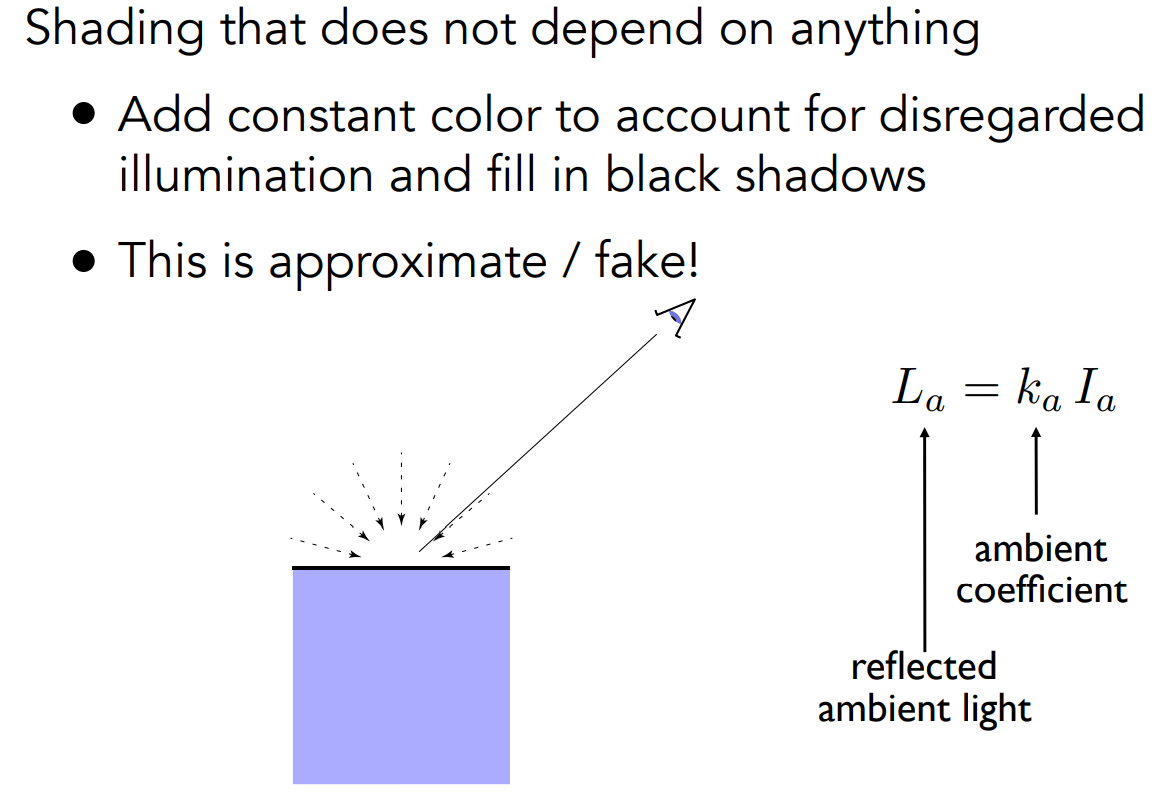
- $L_a = k_aI_a$
- 环境光跟各种方向都无关,可以理解为一个常数——也就是一个颜色
- 环境光的作用:每个地方都有一个基础的颜色,没有任何一个地方是黑的
- 如果想很精确地计算环境光,需要用到全局光照,比较麻烦
Blinn-Phong 反射模型总结

环境光项:一个常数颜色
漫反射项:跟观测方向无关、跟光照和法线角度有关
高光项:在比较少的地方产生的、(通常是)白色亮点
$\begin{array}{ll}L = L_a + L_d + L_s = k_aI_a+k_d (I/r^2)\max(0, \bold {n\cdot l})+k_s(I/r^2)\text{max}(0, \bold n\cdot\bold h)^p\end{array}$
到此,得到了着色模型,考虑任何一个点(shading point)的上色情况。接下来,对每个点做一次着色操作,这样整个场景的所有点就能看到了。
- 实际上,如果一个地方凹下去、环境光会暗一些,但Blinn-Phong模型环境光都是一样的,简化了类似的细节。对于复杂的环境光计算方法,在后面的全局光照部分讲
- “能量”这个说法其实不合理,Blinn-Phong 模型只考虑从光源发射到物体的“能量”损失,观测时不管离多远看上去都是一样的颜色。但事实上,离得远会看起来暗,这些关于radiance的问题会在后面说
Lecture 08 - Shading 2 (Shading, Pipeline and Texture Mapping)
1 - Shading
Blinn-Phong 反射模型定义了每个 shading point 的着色方法:
$\begin{array}{ll}L = L_a + L_d + L_s = k_aI_a+k_d (I/r^2)\max(0, \bold {n\cdot l})+k_s(I/r^2)\text{max}(0, \bold n\cdot\bold h)^p\end{array}$
2 - Shading Frequencies 着色频率
不同的着色频率
着色:应用在一个 shading point 上
着色频率:把着色应用在哪些点上。同一个模型,着色频率不同、结果也大不同
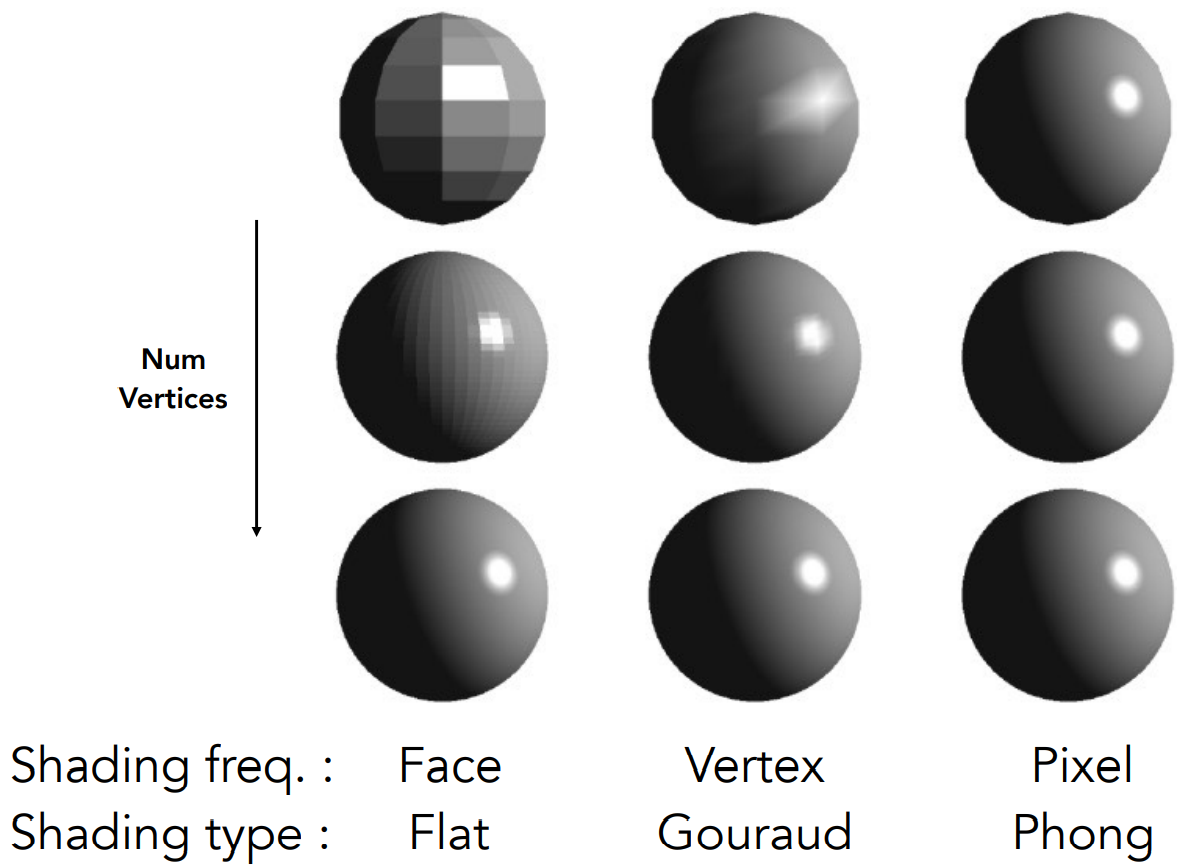
- Flat shading(逐平面):对每个平面只做一次 shading ,每个平面的颜色相同
- Gouraud shading(逐顶点):三角形每个顶点计算法线,对每个顶点做一次 shading;三角形内部进行颜色插值,求颜色
- 引申问题:顶点的法线怎么求?

- Phong shading(逐像素):每个像素上应用 shading。在每个顶点计算法线、在顶点内部插值,得到每个像素自己的法线,分别做 shading
- 引申问题:知道顶点法线,内部的法线怎么插值?

- Flat shading(逐平面):对每个平面只做一次 shading ,每个平面的颜色相同
着色频率的选择
- 对不同着色频率模型,不一定是逐像素着色就是最好的方法。如下图,每列是不同的着色模型,从上到下模型的面数变多。可以看到,如果模型本身比较精细,采用不太精确的着色频率模型,就能得到差不多的结果,不必采用太麻烦的着色频率。取决于具体物体。
其他问题
引申问题:Gouraud模型、Phong模型中,顶点的法线怎么算?
- 任何一个顶点都跟若干三角形相连。因此,把关联平面的法线求平均(由于三角形大小可能不同,可以求加权平均,权是三角形的面积),得到顶点的法线
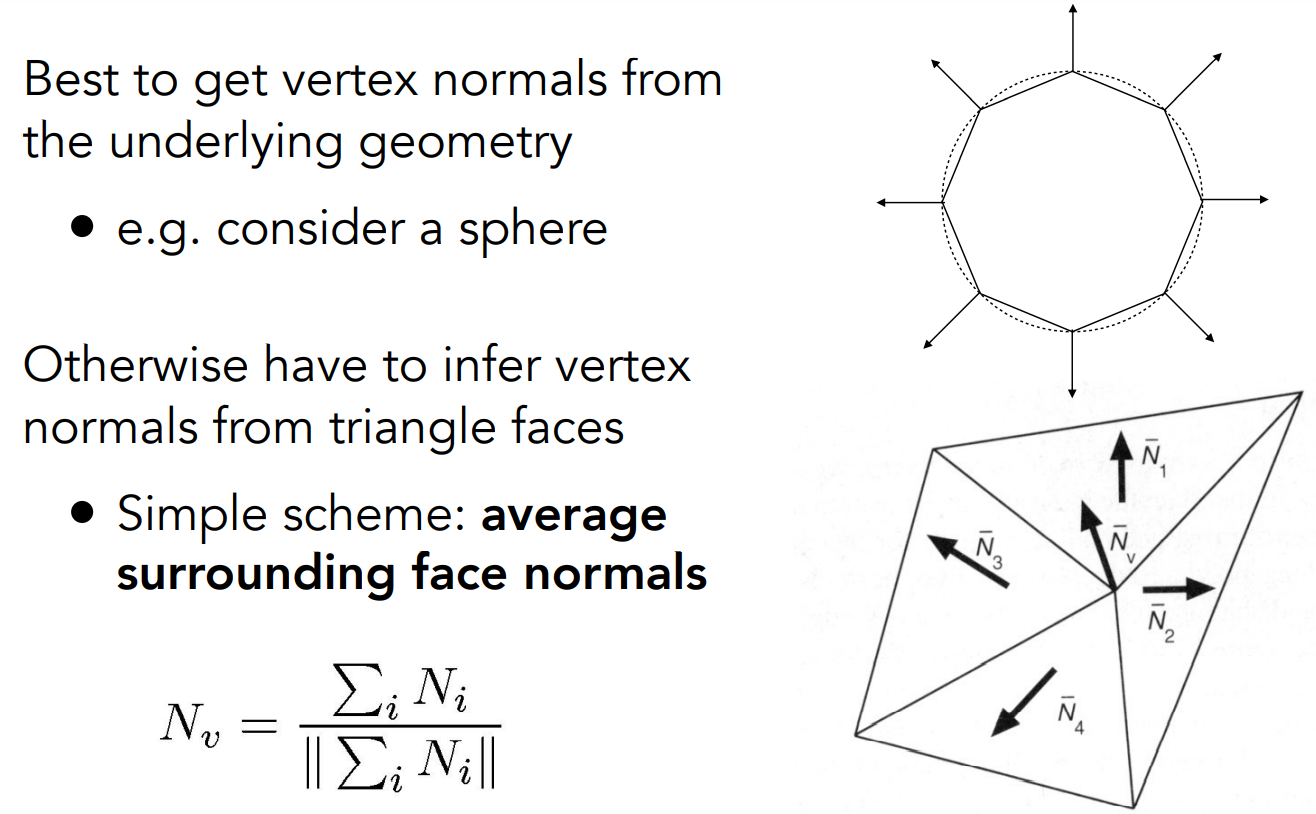
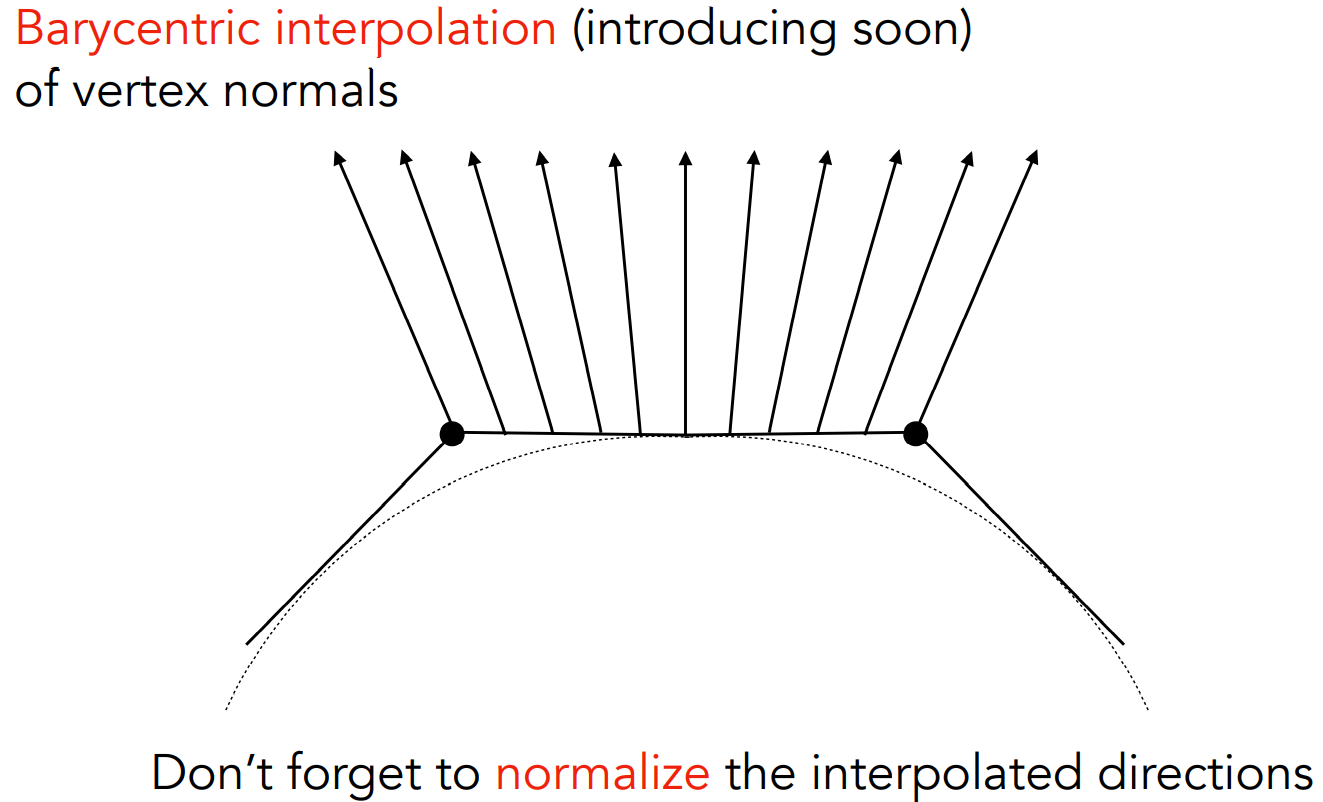
引申问题:Phong模型中,知道顶点法线,内部的法线怎么插值?
- 用到重心坐标
- 注意:所有的法线都是方向,求出来要做归一化、变为单位向量
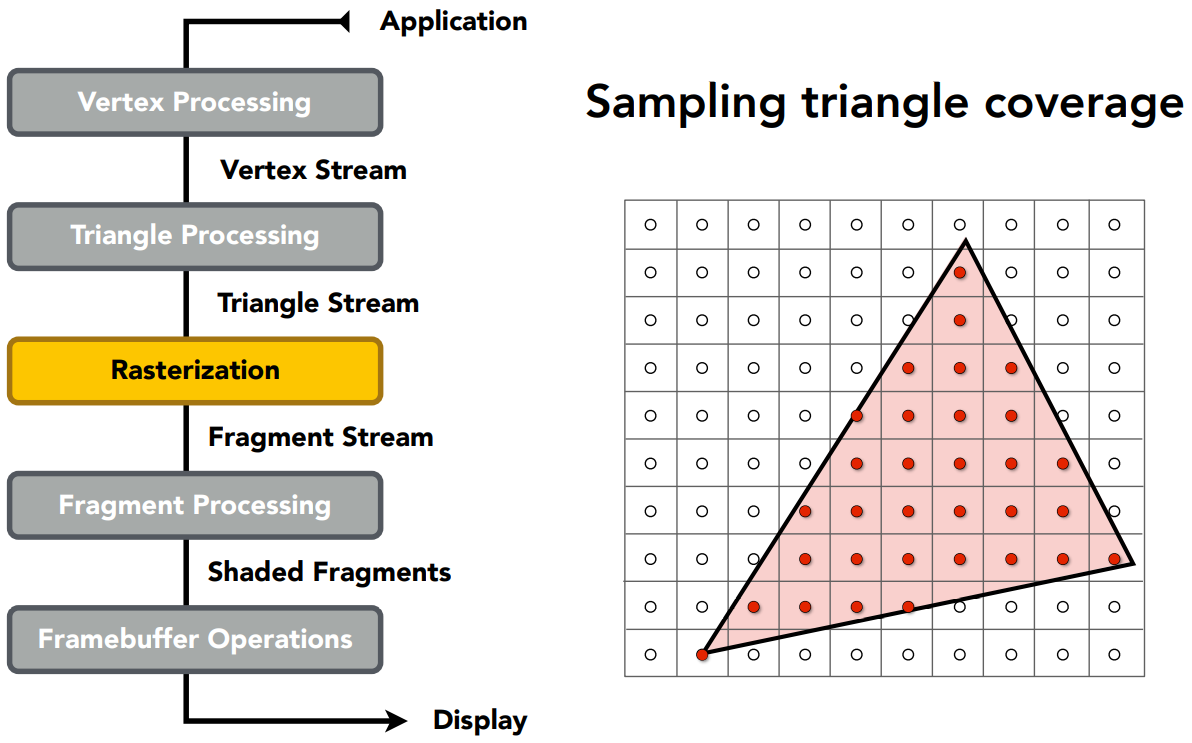
3 - Graphics (Real-time Rendering) Pipeline
实时渲染管线
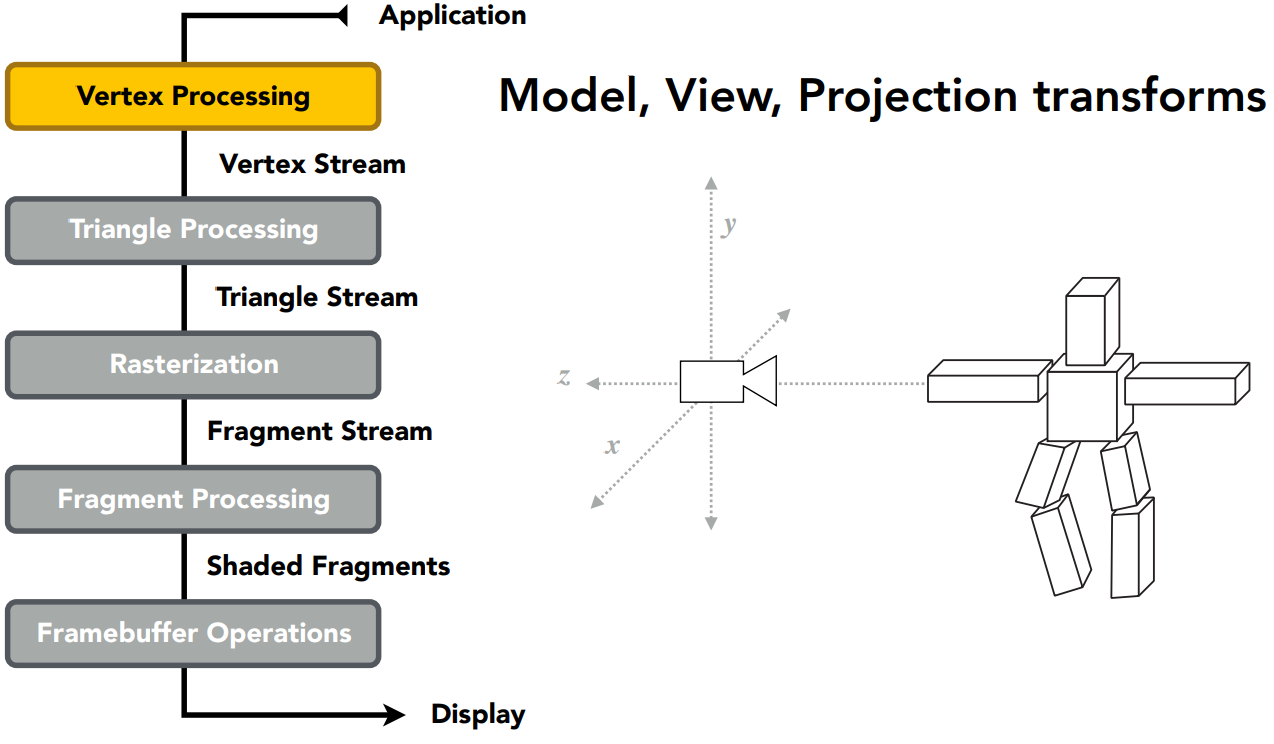
从一个3D场景,如何得到最后的一张图,这个过程就叫做 Pipeline。
- 输入:三维空间中的点
- 经过顶点处理(MVP变换,视口变换等步骤),把这些点投影到屏幕上
- 屏幕上的点会形成三角形
- 经过光栅化(采样,深度测试),把三角形变为若干 fragments
- 每个像素进行着色
- 输出:整个屏幕上所有像素的颜色
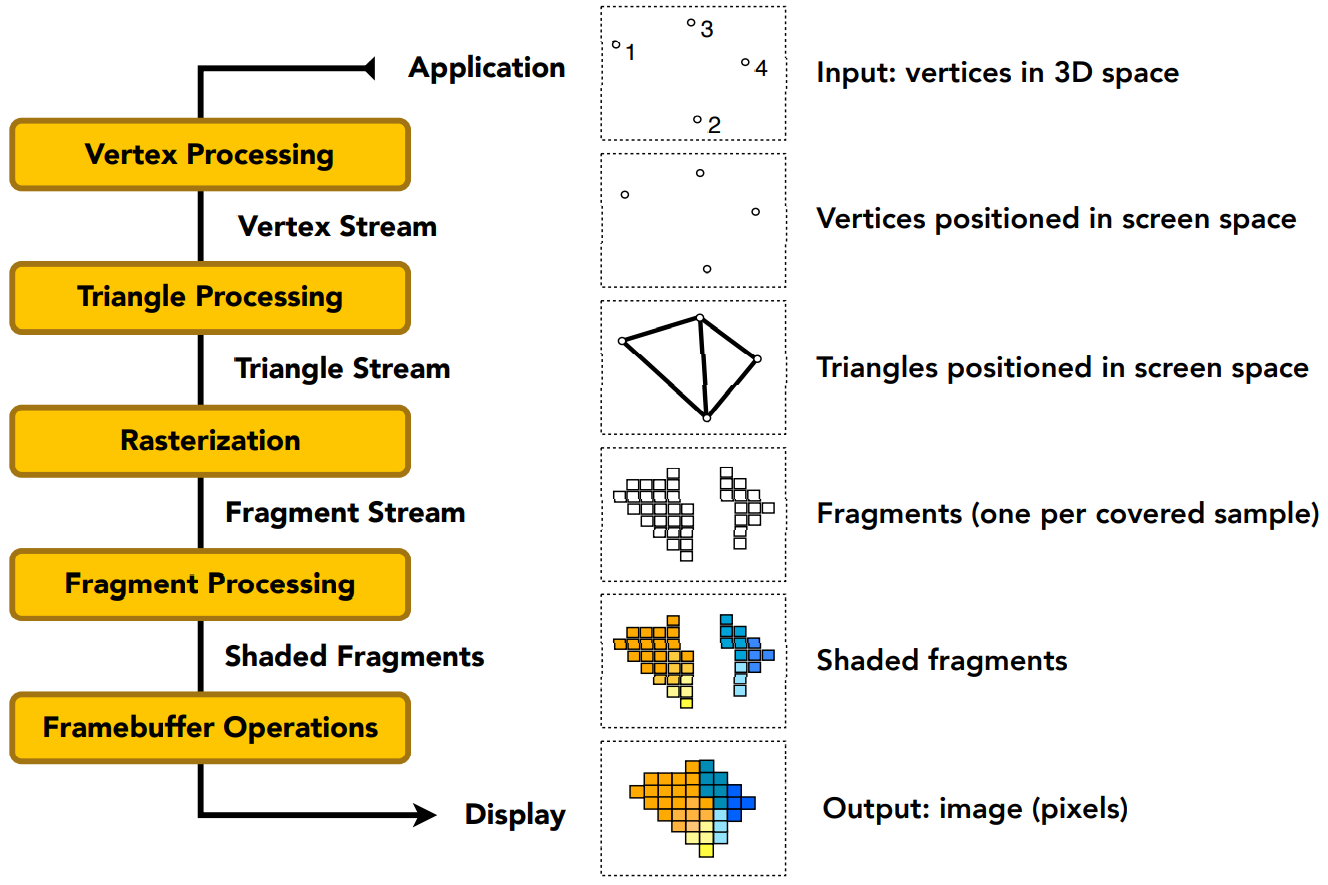
整个操作被写在GPU里。
- MVP变换应用在顶点处理中,对每个顶点做变换
- 对屏幕的像素采样、看是否在三角形内,是光栅化的步骤
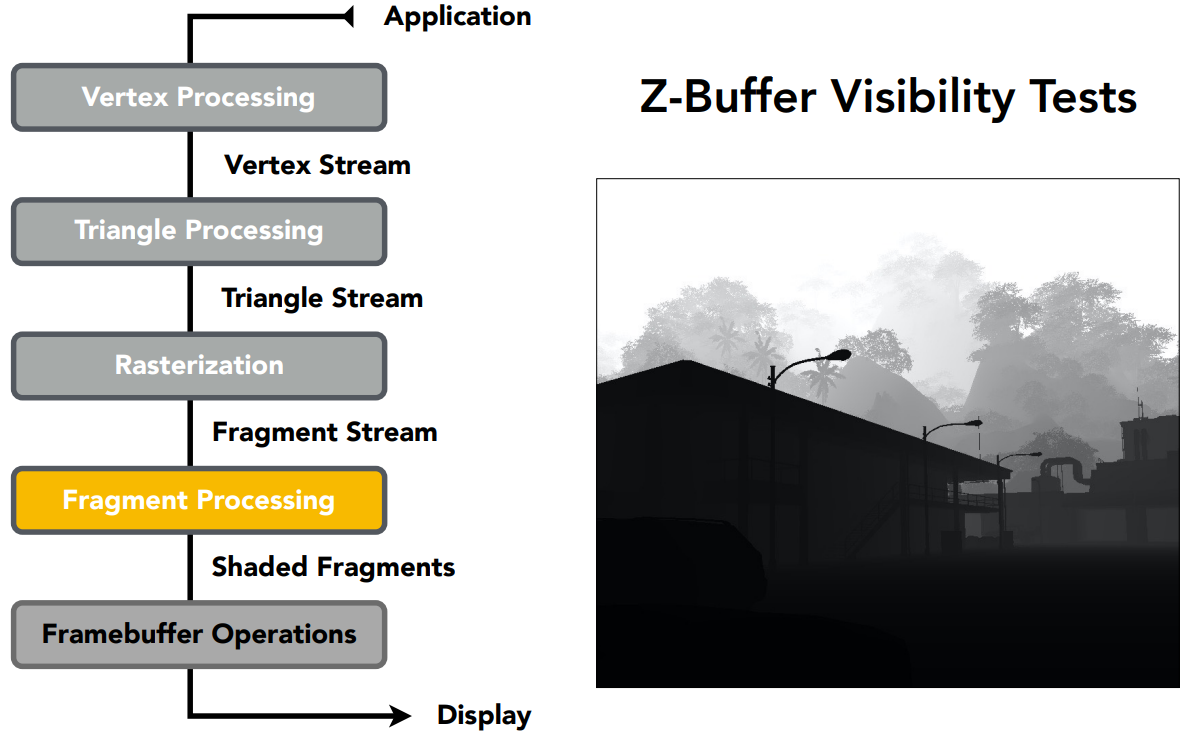
- 光栅化产生了一系列的 fragment(像素)后,使用 Z-Buffer 判断遮挡关系(也可以把这一步划分到光栅化的一部分)
- 如果是逐顶点 Shading,着色会发生在顶点处理中;如果做逐像素 Shading,要等像素都产生后、在 Fragment 里做
- 现代 GPU 是可编程的,可以自定义顶点、像素如何着色。shader 代码控制了顶点和像素是如何着色的
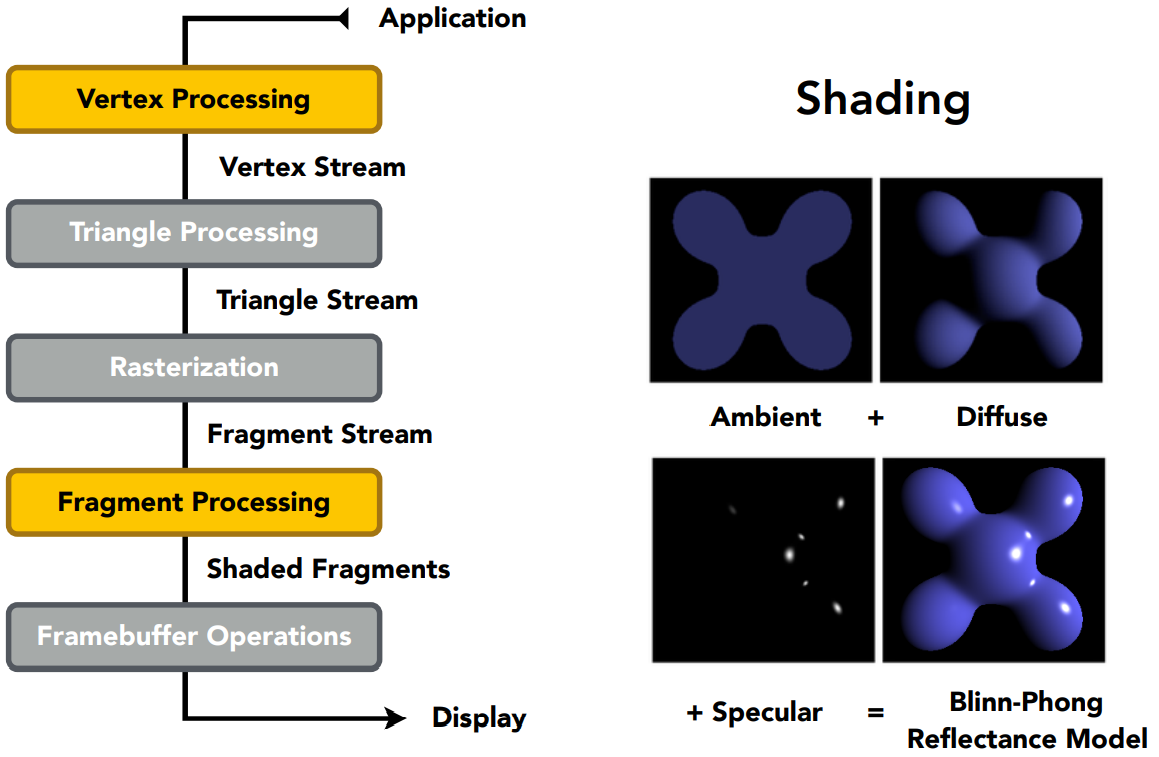
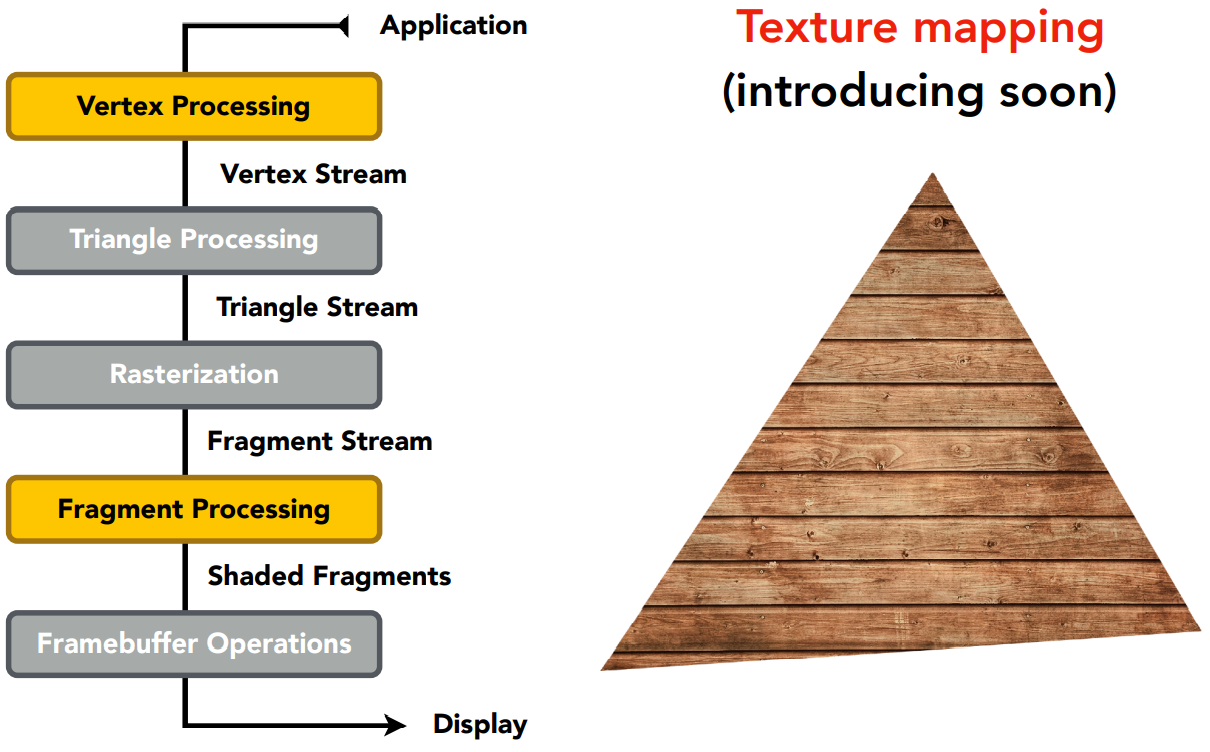
- 三角形内部不同的点拥有不同的属性,显示为纹理,如何做纹理映射在后面说
Shader
现代GPU允许通过shader编程,实现顶点、像素的自定义着色。shader是能够在GPU上直接运行的语言。
- 写的 shader 在意味上是通用的,即每一个顶点或每一个 fragment 都会执行这个 shader,而不需要针对某一个顶点、fragment 特殊定义 shader(不需要写for循环)。
- 如果写的是顶点操作,叫做 vertex shader (顶点着色器);如果写的是像素的操作,叫做 fragment/pixel shader(像素着色器)。
- 对于像素着色器,要计算并输出像素最后的颜色
uniform sampler2D myTexture; // 全局变量,纹理
uniform vec3 lightDir; // 全局变量,光照方向
varying vec2 uv; // interp. by rasterizer
varying vec3 norm; // 顶点的法线,interp. by rasterizer
void diffuseShader()
{
// 通过纹理,得到该点的漫反射系数 kd
vec3 kd;
kd = texture2d(myTexture, uv);
// 漫反射系数 * (光照方向、法线方向的点乘,限定在[0,1])。即漫反射项,或者是 Lambetrtian shading model
kd *= clamp(dot(-lightDir, norm), 0.0, 1.0);
// 存储这个值,输出 fragment 的颜色
gl_FragColor = vec4(kd, 1.0);
}一个网站:ShaderToy,免去OpenGL、DirectX等,只需写着色器即可,可以在网页上执行并产生结果。
- 这个蜗牛的所有几何形体都是通过数学方法定义的,没有用到任何的三角形
- 这个例子是几何形体的投影,跟三角形的投影不一样
现代图形学的发展
- 现代GPU高度并行,显卡可以同时处理大量几何、并且着色非常快。
- 现在的发展趋势:超级复杂的场景,游戏引擎集合各种模块,尤其是图形渲染模块
- GPU是整个一套渲染管线的硬件实现,shader这部分是可编程的。除了vertex shader、fragment shader,现在还有geometry shader来做几何的计算,compute shader来做通用的计算。
- GPU理解为高度并行的处理器
4 - Texture Mapping 纹理映射
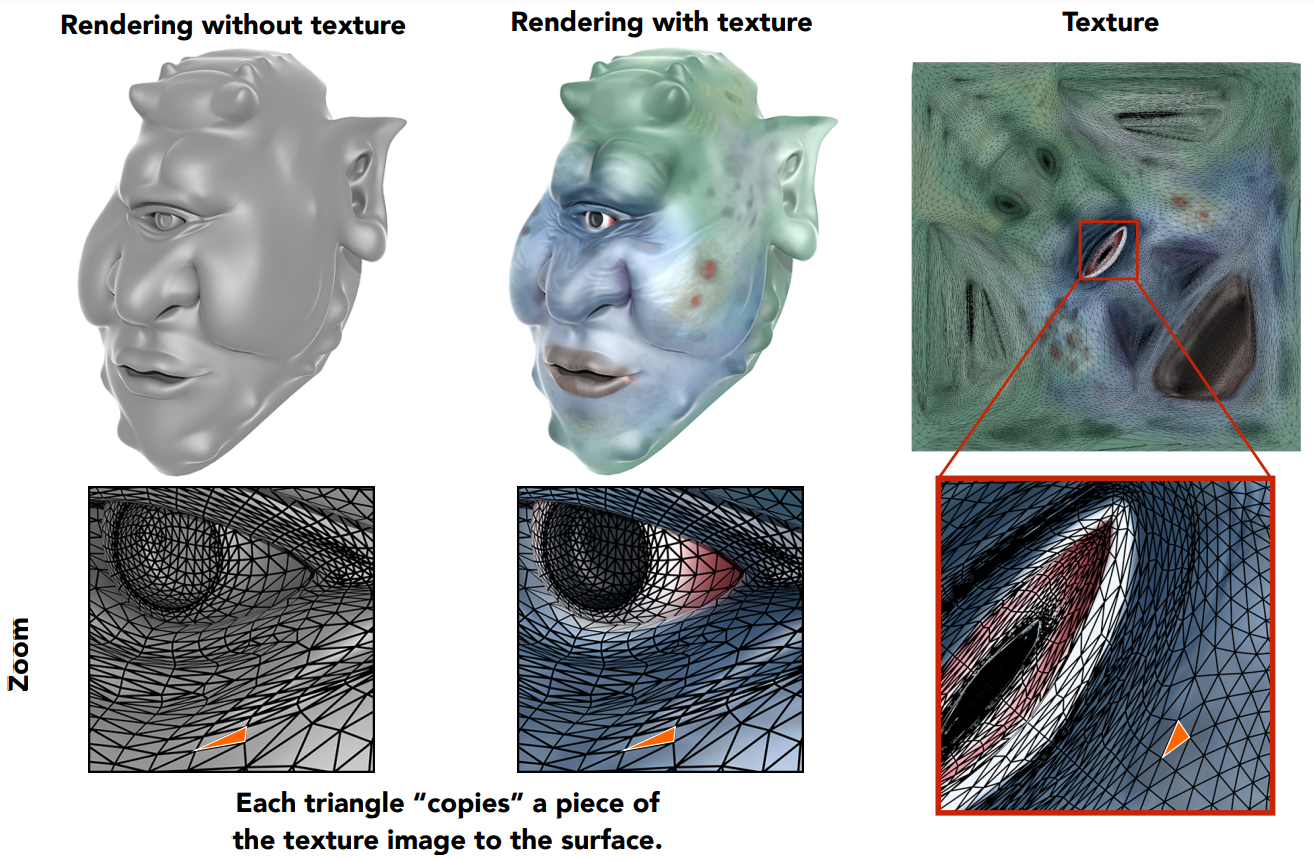
如何对三角形内部进行填充?引入纹理映射的思路:希望在物体的不同位置定义不同的属性。
纹理定义了一个物体上任意一个点的属性。有了这些属性,在着色时,各个点就可以被差异化着色。
纹理图
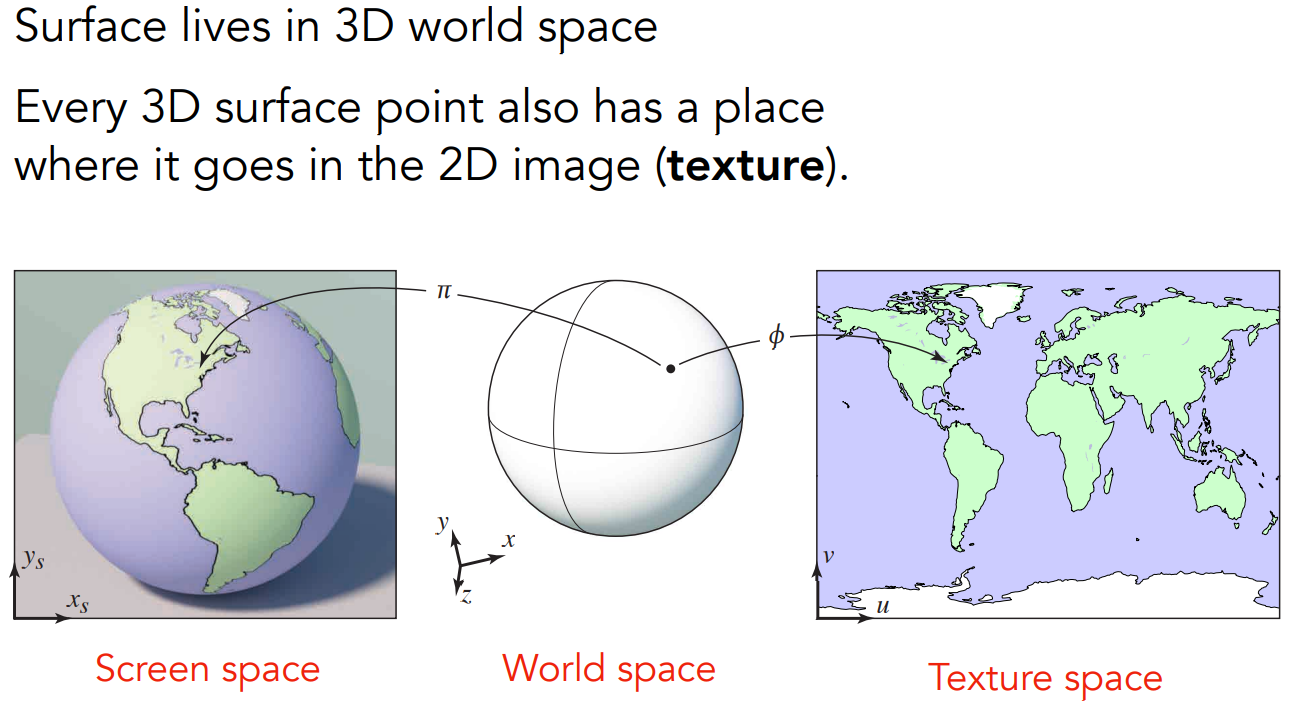
现象:任何一个3D物体的表面都是2D的。也就是说,3D物体的表面跟一张图有映射关系。
纹理就是一张图。可以对纹理进行一系列变换,或取一部分,蒙在3D物体的表面。物体表面上的点跟纹理图上的点之间的关系就是纹理映射。
一般是美工做这个步骤:
- 通过先建模、再把模型展开,放到纹理图上的某个位置进行对应
- 自动化的过程:给任意模型,把它展开成一个平面,并且产生的三角形尽可能得少扭曲。这是图形学中几何的一个研究方向 parameterization(参数化)
纹理映射
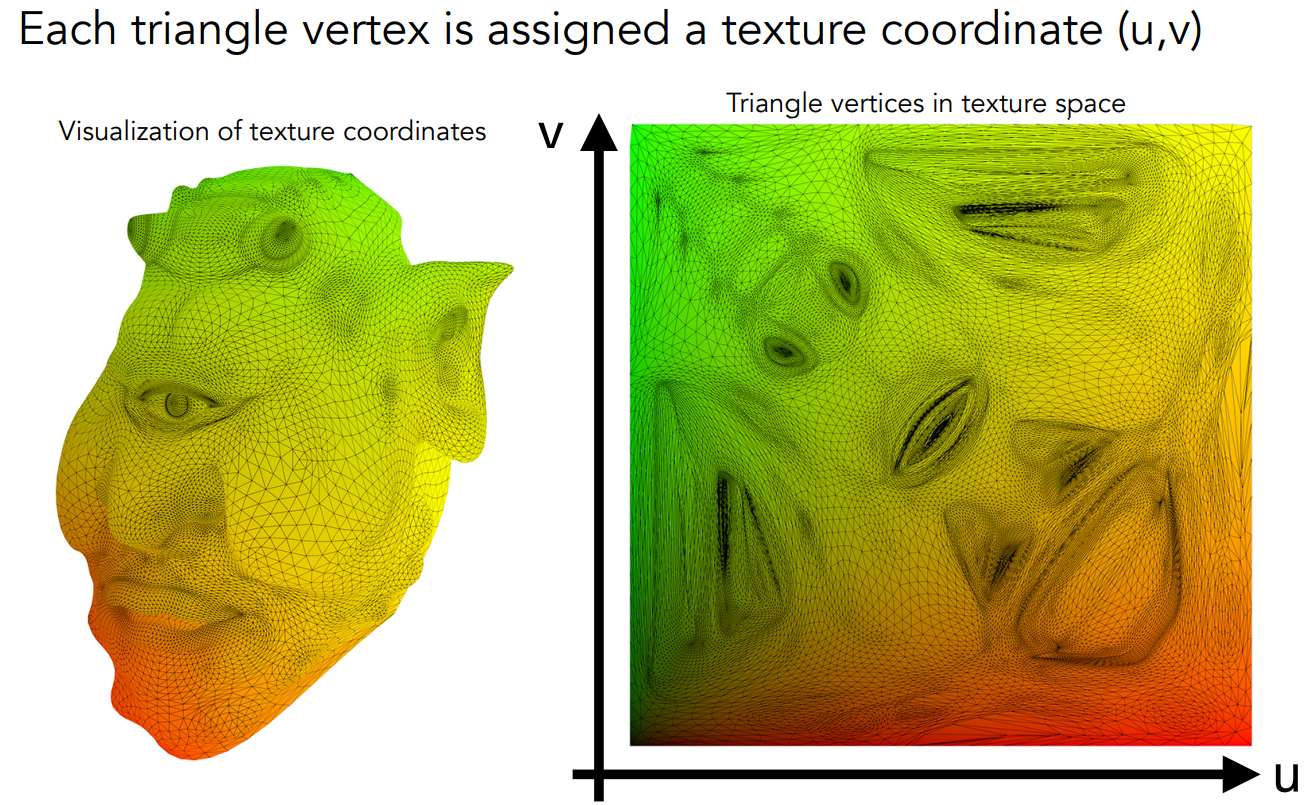
不管怎么把空间中的三角形映射到纹理上,本课我们认为已经有了这个映射关系。对于三角形上的每个顶点,我们都知道它对应在纹理上的一个坐标。
纹理图上的坐标系:$(u, v)$ 。通常,不管分辨率、长宽比,都约定 $u,v \in [0, 1]$ 。
纹理并不是只能用一次,可以让纹理重复多次、把场景贴满(tile,或许unity2d的tilemap也是这样?)。纹理如果设计得好,可以使纹理在复制时无缝衔接。
下一个问题:知道了三角形的三个顶点对应的纹理坐标 $(u, v)$,如何做三角形内部的插值?(三角形的顶点具有不同的属性,如何得到三角形内部点的属性?需要用到重心坐标。)
Lecture 09 - Shading 3 (Texture Mapping cont.)
前两节shading课,讲了blinn-phong反射模型、着色模型和着色频率、图形渲染管线、纹理映射。不同的材质的平面、不同的光线作用,会产生不同的着色结果。
着色的基本已经讲完了。本课是关于纹理的一些应用。
- Barycentric coordinates
- Texture queries
- Applications of textures
- (Shadow Mapping)
1 - 重心坐标(Barycentric Coordinates):在三角形内部进行任何属性的插值
关于插值
为什么会用到三角形插值:很多东西是在顶点上计算的,需要在三角形内部得到平滑的过渡
插值什么内容:纹理映射中的$(u,v)$坐标;顶点的颜色(逐顶点shading);顶点的法向量(逐像素shading)
为了实现插值,需要引入重心坐标
重心坐标
- 每个三角形定义一套重心坐标(换一个三角形,就换一套重心坐标)
- 定义:在 $\triangle ABC$ 的平面内任意一点,都可以表示为 $A,B,C$ 三点的线性组合,且线性组合的系数 $\alpha,\beta,\gamma$ 相加为 1
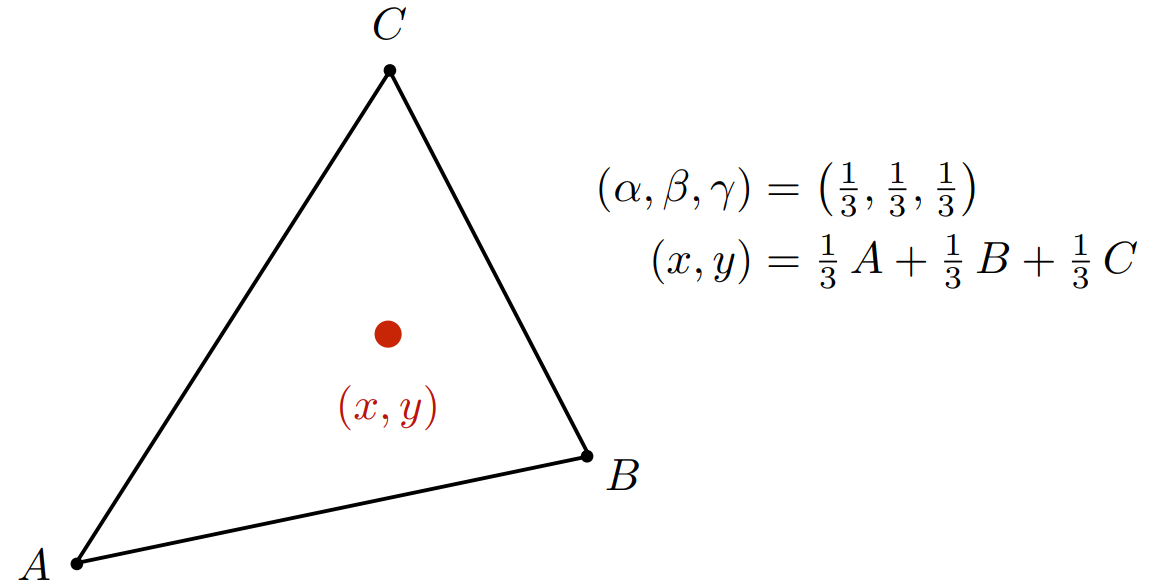
- $(x, y)=\alpha A + \beta B + \gamma C\space,\space\alpha+\beta+\gamma=1$
- 如果某点的 $\alpha,\beta,\gamma$ 相加为 1,且都是非负数,则这个点在三角形内部
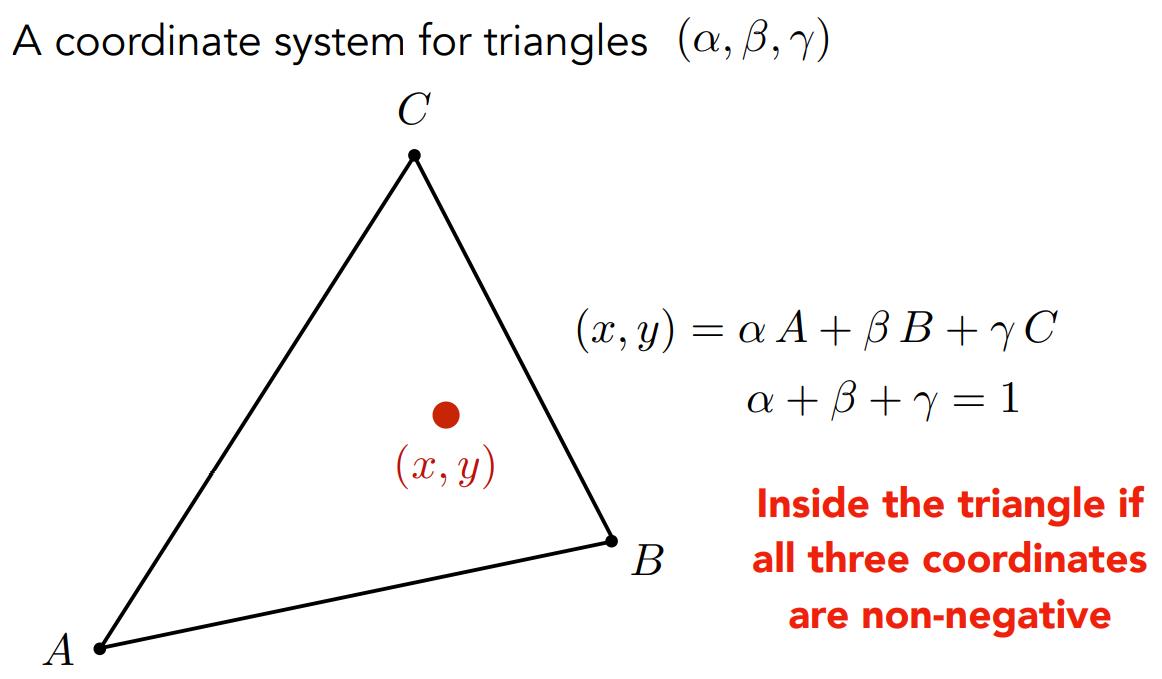
- 计算:可以通过每个顶点“对面”的三角形的面积来计算 $\alpha,\beta,\gamma$
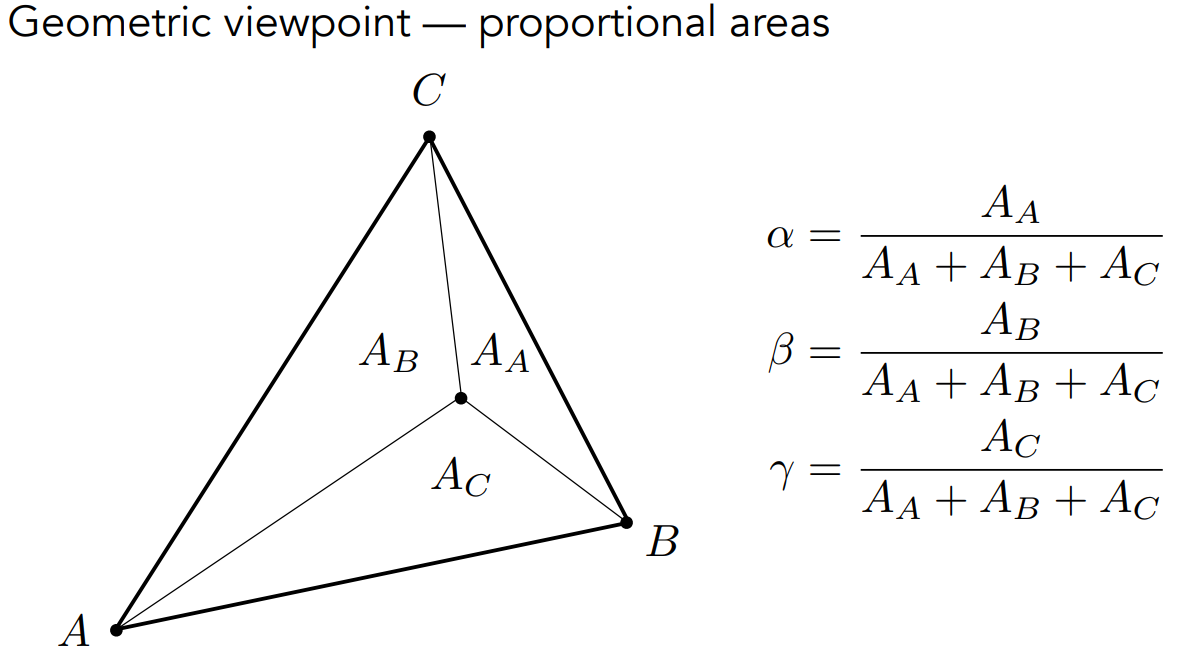
- 由面积公式,可以简化计算成坐标形式:
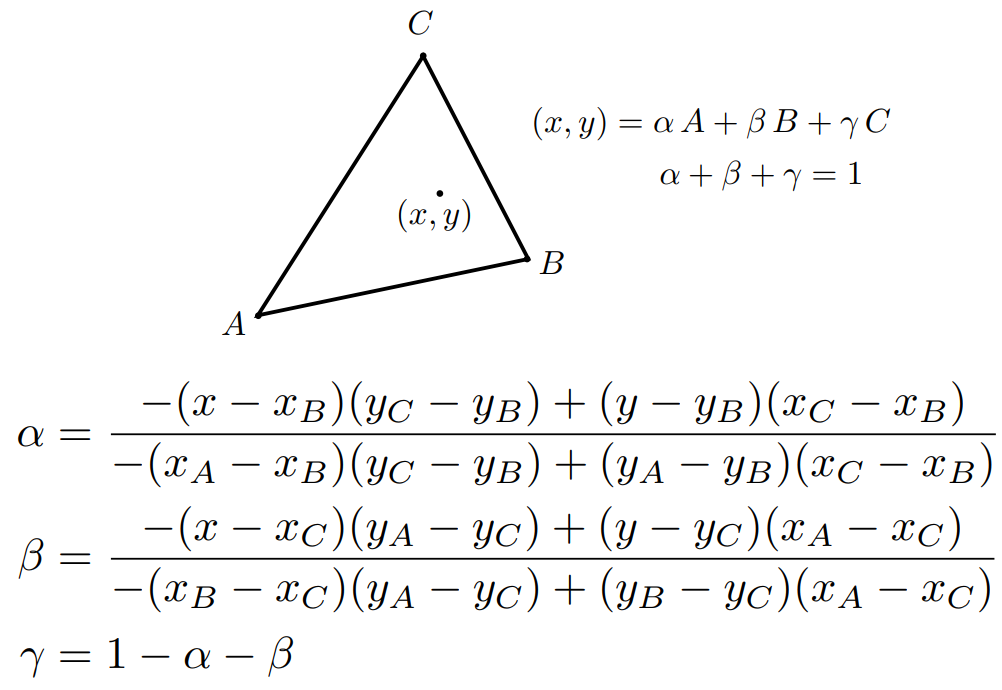
- 举例:三角形的重心(centroid),把三角形分成面积相同的三块
图形学的插值和重心坐标
在图形学中,需要插值的属性,同样应该使用重心坐标进行线性组合。
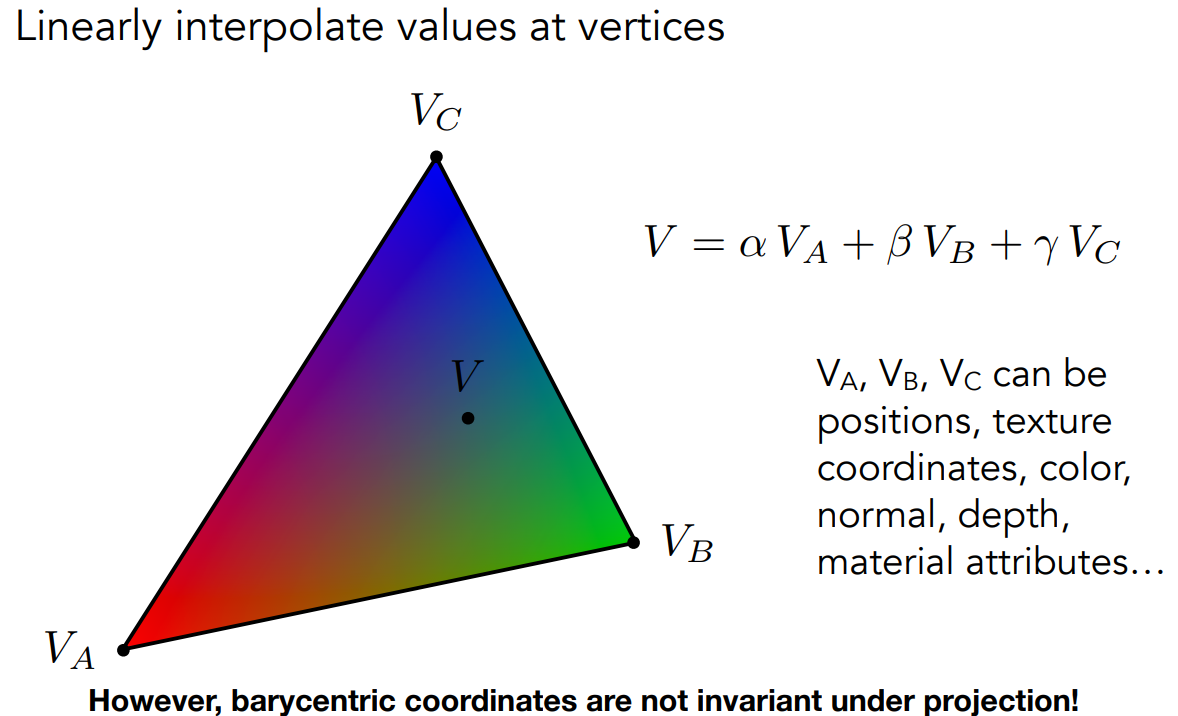
使用重心坐标,可以通过顶点坐标,计算出插线性插值的参数。从而实现任意一点的插值。
注意:投影变换中,重心坐标可能改变(空间中的三角形投影到平面上,如果三角形发生变化、重心坐标自然发生变化)
- 因此,如果插值3D空间中的属性,需要在3D中进行重心坐标的插值,而不是投影后在新的三角形内做插值
- 主要应用在:光栅化计算深度。在光栅化过程中,要应用逆变换(从2D变换回投影前)、求得像素在3D空间的深度
2 - 纹理放大(Texture Magnification)
2.1 在渲染中应用纹理
屏幕中的任一个采样点(像素或MSAA等细分),都有一个位置,在这个位置上可以插值出 $(u,v)$ 纹理坐标。通过纹理坐标查询纹理图,纹理在该点的值可以当作漫反射系数 $K_d$。
在此过程中,可能出现一些问题。
2.2 纹理本身太小,怎么办?(双线性插值)
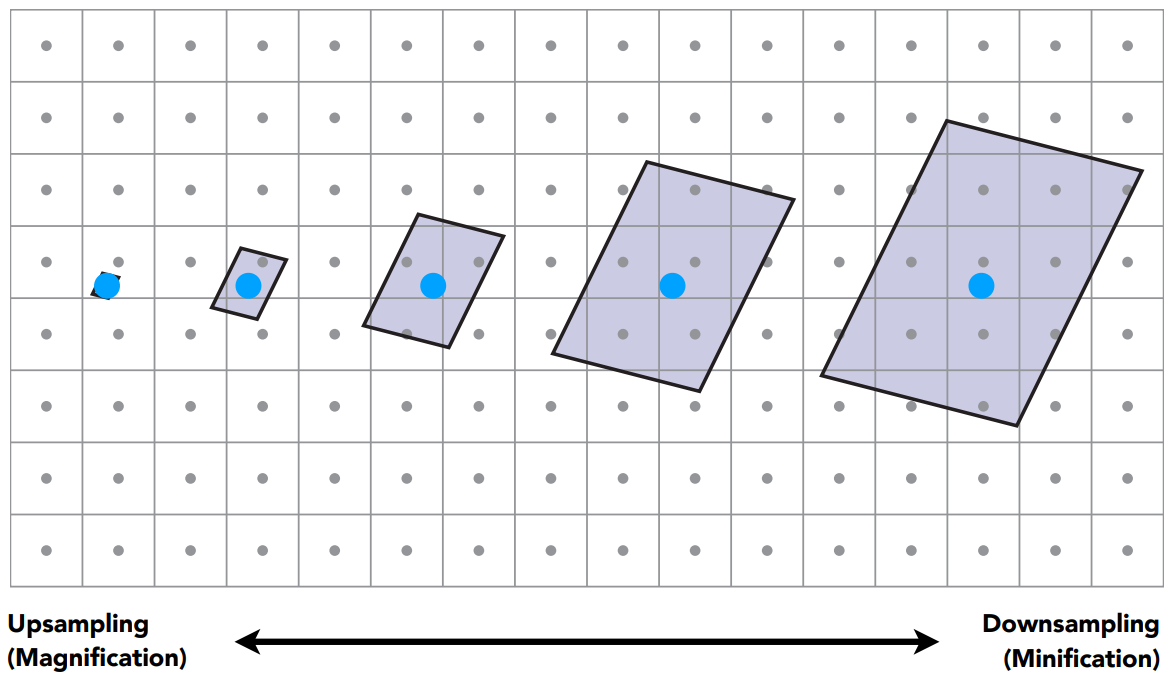
纹理本身太小,画面分辨率太高(高清的模型,使用低清的纹理),像素的中心映射到纹理非整数的位置上。
最邻近映射
- 不管投影到何处,都当作离得最近的纹理坐标的值
- 导致很多地方映射到同样的纹理坐标位置上,出现格子
双线性插值(Bilinear interpolation)
- 定义1D的插值操作
- 以图中情况为例,先在水平方向上,插值计算 $u_0,u_1$ 点的值
- 然后在竖直方向上,插值计算红点处的值
- 因此,红点处的值综合考虑了周围四个点的值,并且结果是根据距离的线性插值
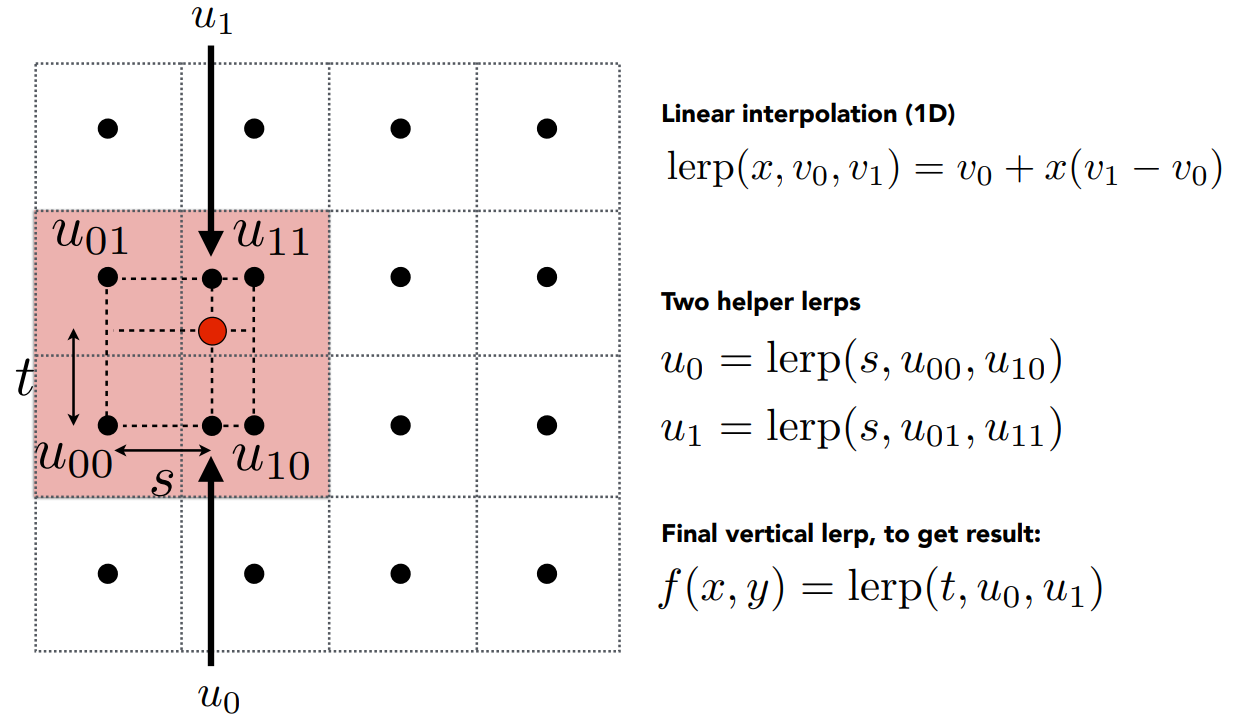
更高次的插值,比如取临近 16 个点的 Bicubic interpolation,进行 3 次插值,能得到更好的结果。
好的质量都伴随更高的开销,双线性插值在能接受的计算量上得到了不错的结果。

2.3 纹理本身太大,怎么办?(Mipmap 和三线性插值)
问题
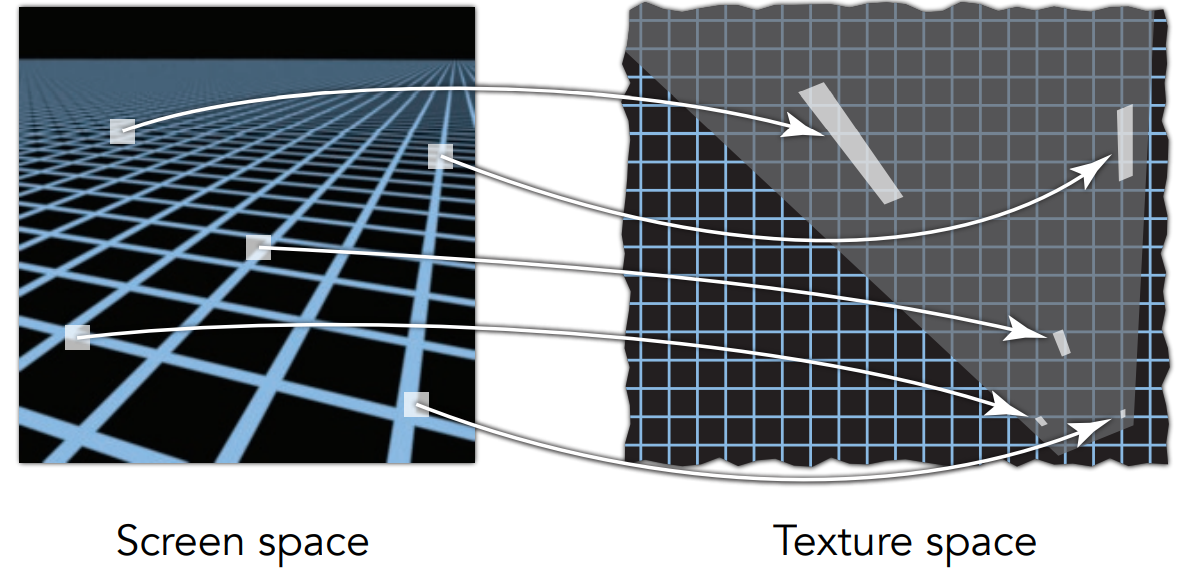
在透视投影中,如果还按照每个点在纹理图上寻找坐标的方法进行着色,远处有摩尔纹、近处有锯齿,产生了走样(aliasing)。
产生这种现象的原因:
- 由于透视投影,近处的像素覆盖的纹理小,远处的像素覆盖的纹理大,不同像素覆盖的纹理大小各不相同
- 像素覆盖的纹理小,查询像素中心的纹理值即可
- 像素覆盖的纹理大(因为纹理图大),像素中心的纹理值,认为是覆盖的整块纹理区域的平均值。在这种情况下,不能简单地使用像素中心来采样
理论上如何分析这个问题?
- 走样问题:信号变化过快,采样的频率跟不上信号变化的速度。
- 当纹理特别大,像素内部会包含变化的纹理(单个像素覆盖一块纹理)。像素内频率高,但只用像素一个采样点,就发生了走样
- 因此,需要在像素内使用更高频的采样方法
- MSAA的思路:对于一个像素,用更多的采样点采样,再取每个像素的平均。这里也可以这样做,比如每个像素取512个采样点,但会让计算代价变大。
- 另一个思路:采样会引起走样,是否能不采样?即:立刻可以知道纹理图一个区域的值的平均,不进行采样。
- 算法问题:点查询问题(Point Query,给定一个点,求它的值。之前的双线性插值等)和范围查询问题(Range Query,给定一个区域,不做点采样立刻得到它的范围内平均值或最值)
- 引入概念:Mipmap
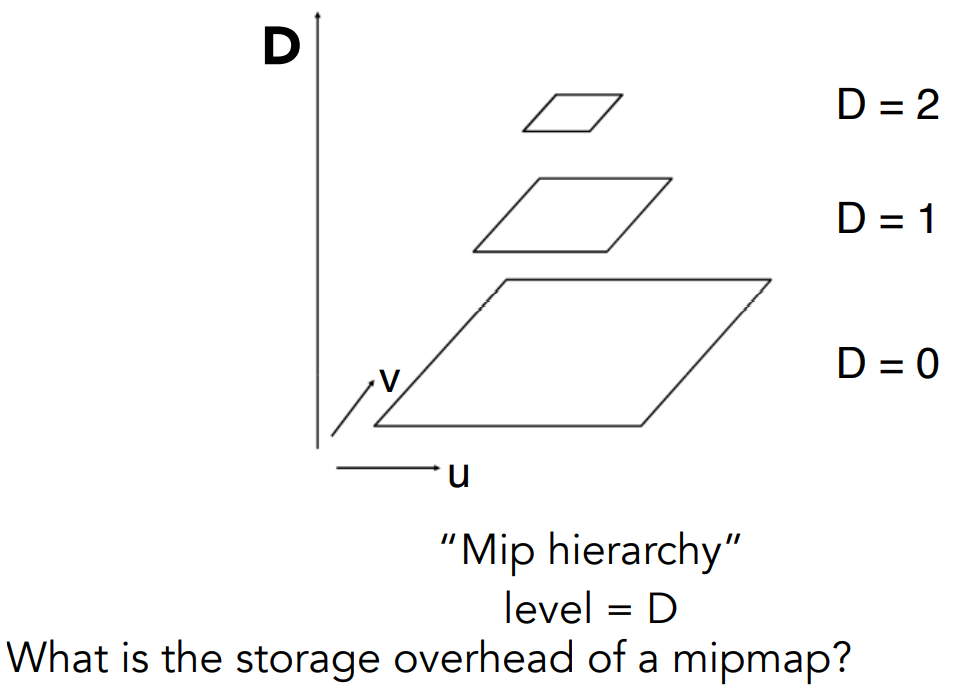
Mipmap:进行范围查询
特点:fast(查得快)、approx.(查到的是近似值)、square(仅能做正方形查询)
拿到一个纹理作为第0层,之后的每层把上层的分辨率缩小一半。共有log层。
提前计算一个纹理对应的mipmap
在CV中,叫 image pyramid,两者是相同的概念
一个小问题:总共引入了多少额外的存储?
- 级数求和问题,$1+\frac{1}{4}+\frac{1}{16}+… = \frac{4}{3}$
- 只多了三分之一的存储量
mipmap的查询
- 首先,可以通过近似,把像素覆盖的纹理范围近似成一个正方形
- 可以根据相邻像素中心在纹理图上的坐标,求得像素两个方向上的变化趋势
- 可以把两个方向上比较大的变化趋势,作为正方形的长度
- 由这一步,可以得到任何一个像素,覆盖的纹理图的正方形范围
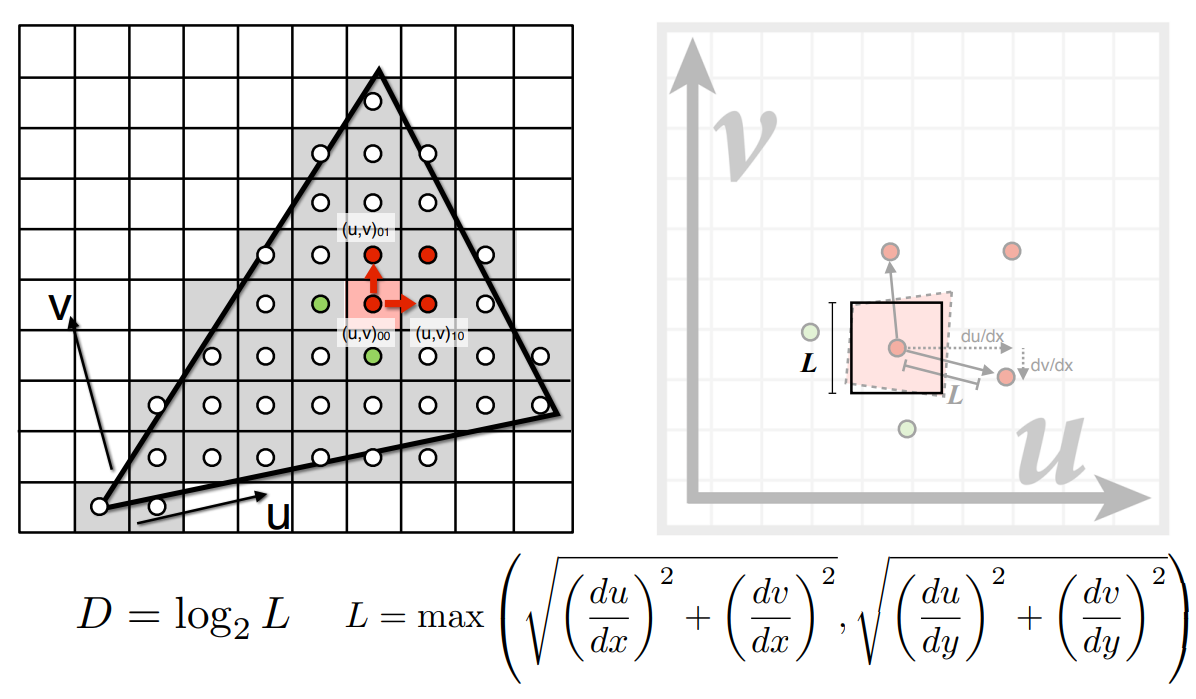
- 然后,由 mipmap 的计算方法,在 mipmap 的 $D=\log_2L$ 层查找这个像素的纹理平均值
- 如计算出像素对应正方形为 $4\times 4$,就可以在 mipmap 的第二层找到平均值
- 在某一层上的查询,依然是 bilinear interpolation(覆盖的正方形不一定正好是 mipmap 的一个格子,而可能覆盖在四个格子上)

- 如图,离得近的位置,每个像素的纹理在低层的 mipmap 查询;离得远就在高层查询。即由于近大远小,在远处,一个像素表达的信息更多,覆盖的纹理范围大,才会近似一个区域
- 另一个问题:在哪一层 mipmap 上查并不连续,而是跳跃的,图中不同颜色没有渐变,在 shading 时可能会在不同层之间看到缝隙。
- 引入 Trilinear Interpolation(三线性插值,mipmap 层与层之间的插值),来解决这个问题。这样,可以通过第一层、第二层,得到第 1.8 层的 mipmap
Trilinear Interpolation(三线性插值)
- 如:查询1.8层某个点的纹理值
- 分别在第一层、第二层内,做该点相同位置的 Bilinear Interpolation(水平、竖直方向的两次插值)
- 将这两层、两个点的查询结果再做一个插值(层与层之间的第三次插值)
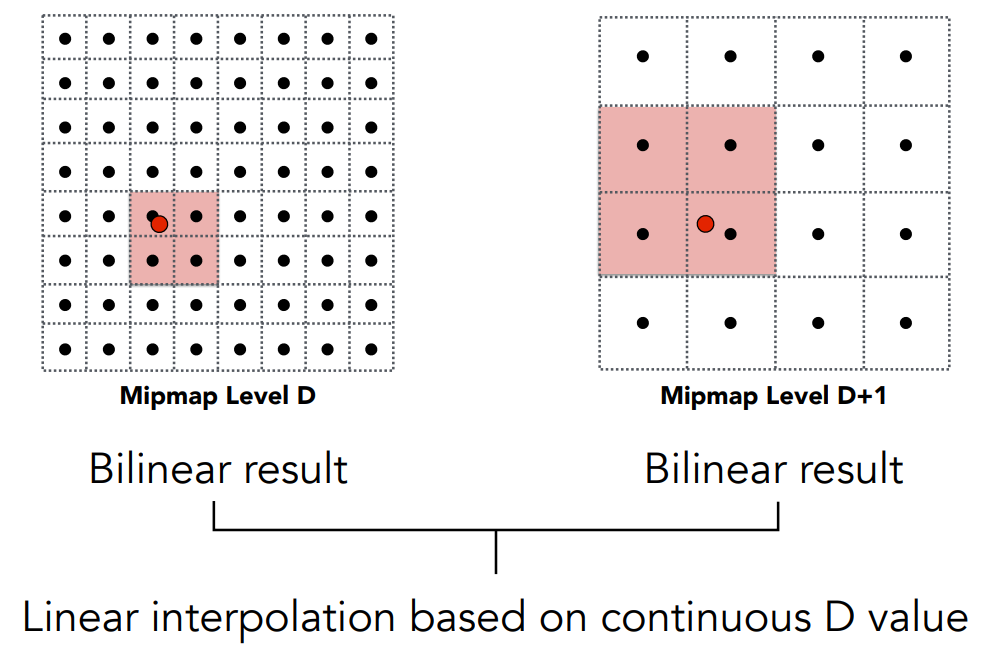
- 到此为止,在纹理的内部,可以双线性插值得到平滑的值;在任意 mipmap 层,也可以三线性插值得到平滑的值。从一张纹理图,可以得到完全连续的纹理表达
- 对于任意像素覆盖的区域,只需要通过一次三线性插值查询,就可以得到这块区域覆盖的纹理的平均值了
三线性插值可以做到完全连续的表达,并且通过两次查询(两层mipmap)、一次插值(层之间),用很小的开销,得到任意一点的纹理查询,目前被广泛应用。
其他思考
再思考回来:mipmap能否完全解决问题?在远处,mipmap 会导致 overblue 现象。
问题出在哪里?mipmap 的查询就是三线性插值计算,没有问题。因此,问题在于 mipmap 本身的限定条件:只能查询方块,得到近似结果。
正常的映射中,一个像素会映射到纹理上的各种形状,如图,有长条形的、斜着的区域。 用正方形近似计算会不准确。
使用 Anisotropic Filtering(各向异性过滤),可以解决三线性插值的一部分问题。

- 各向异性:在不同方向上表现各不相同。各向同性:矩形在水平竖直方向上表现完全相同
- 图片的右上方,Mipmap 可以看作是对角线上的一系列变换,只能查询正方形的区域
- 各向异性过滤则会生成图中一系列水平竖直“压扁”的图片,称为 Ripmap,额外开销是原来的 3倍
- 对比 Mipmap,额外开销仅三分之一
- 各向异性过滤允许对长条形的区域做查询,但依然不能查询斜着的区域
- 游戏中有各向异性的选项,其中的参数 $n$x,说明计算到第 $n$ 层,即从左上角开始 $n*n$ 的区域,因此最终都收敛到三倍。各向异性的存储量跟开多少 x 关系不大,显卡的显存足够即可,跟计算力无关
此时,可以使用 EWA过滤 等方法
- 任意不规则形状,都可以拆成很多不同圆形,来覆盖这个不规则形状
- 每次查询一个圆形,多次查询就能覆盖不规则形状
- 代价:多次查询
3 - 纹理的应用
在之前,把纹理想成颜色,就是漫反射的 $K_d$ 系数。实际上,纹理可以定义任何的属性。
在现代GPU中,可以把纹理理解为一块内存,可以对这块内存做快速的点查询、范围查询,或做滤波。简单来说,不必把纹理理解为图像,可以理解为一块数据,可以做不同类型的查询。
从这个角度,纹理可以表示很多东西:
应用一:Environment Map/Lighting
纹理作为环境贴图 / 环境光照,用纹理定义环境光
- 任何一个方向都可以看到光,不管是直接光照、光源还是反射来的光。人看到的物体都是光照反射到人眼。
- 把任何方向来的光都记录下来,就是环境贴图。用纹理描述整个环境光是什么样子,然后可以用这个纹理去渲染别的物体
- 假设:环境光来自无限远处,只记录方向信息、不在意深度
- 左图:在屋子里四面八方看到的东西;右图:茶壶反射了这个环境光

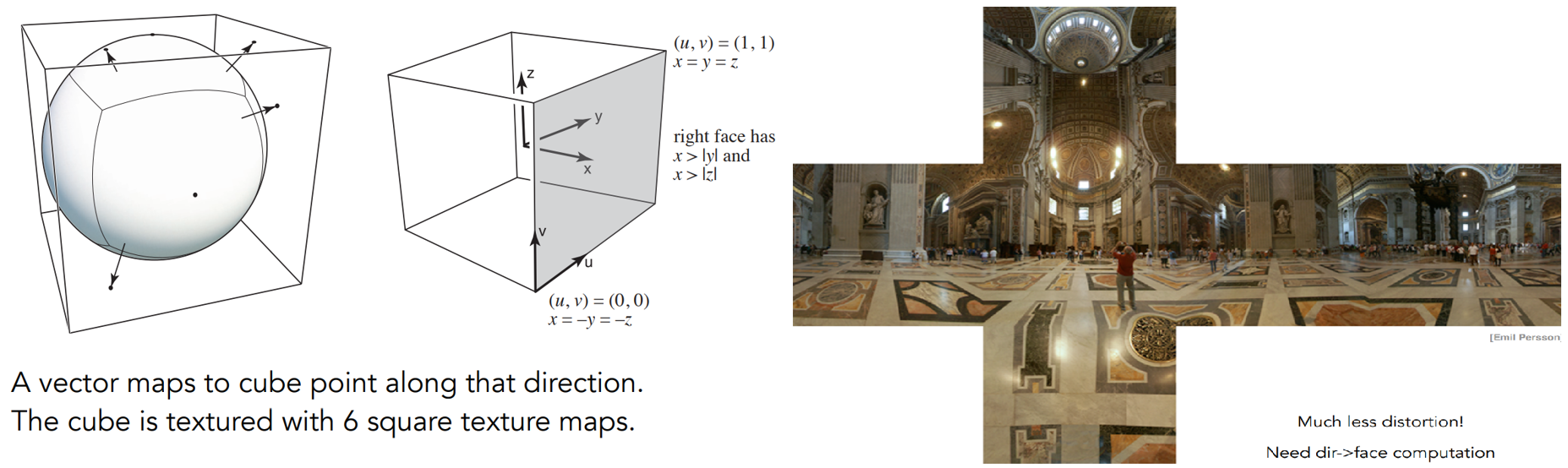
- 可以把整个环境光记录在球上,然后展开:Spherical Environment Map。但展开后的图会发生扭曲
- 为了解决扭曲,在球外加一个立方体包围盒,从球心延申到立方体上,用立方体记录环境光:Cube Map。
应用二:Bump Mapping
纹理作为凹凸贴图 / 法线贴图,纹理存储点在法线方向的相对高度
- 在不增加几何模型复杂度的情况下(依然是一个球),可以通过应用复杂的纹理,定义一个点的相对高度,从而让法线发生变化、着色的明暗发生变化,实现图右的凹凸效果。
具体方法:
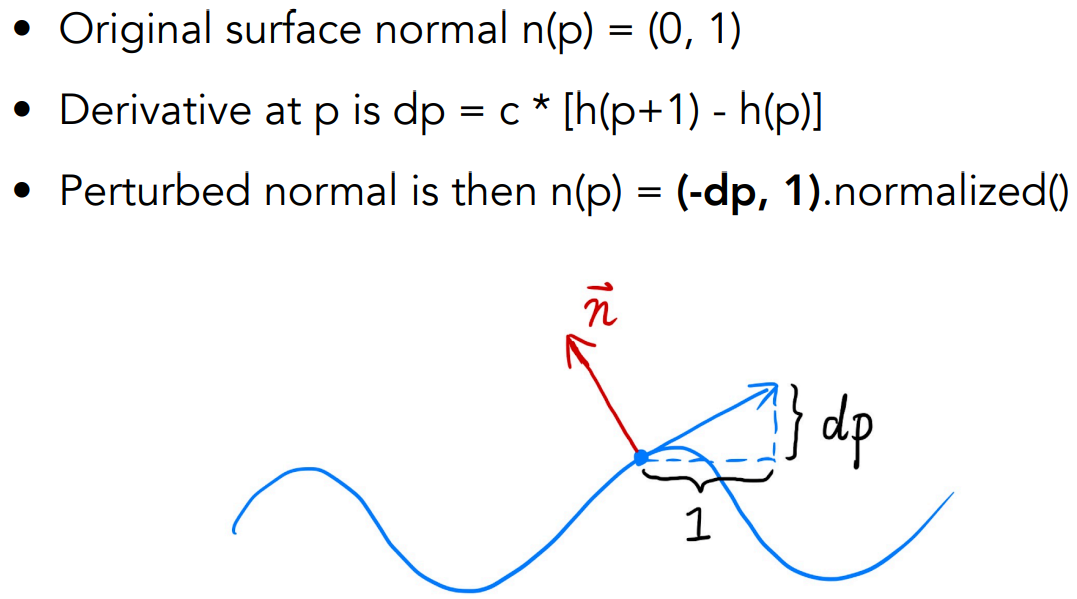
flatland case:通过凹凸贴图,给光滑的表面加上高度的变化,让点的法线发生扰动。

- 计算方法:可以根据差分方法,近似计算切线方向 $(1, dp)$,再根据垂直关系求得法线方向 $(-dp, 1)$ 。$c$ 是相关系数,越大说明凹凸贴图效果越强
- $dp$ 使用相邻两点的高度差计算
3D case:也一样,在两个方向求导数
- 为了方便,会假设原来的法线方向是 $(0,0,1)$,也就是在局部坐标系里进行计算,通过纹理映射修改法线方向、然后再计算回世界坐标。涉及到一个简单的坐标变换,在HW3里用到

更现代化的做法:Displacement mapping(位移贴图),跟凹凸贴图类似,纹理都是记录一个点的相对高度
位移贴图会真的做位置移动,真的移动了顶点的位置。改变了几何
凹凸贴图会根据位置移动,换算成法线的变化,然后做假的顶点运动。没有真的改变几何
下图中,凹凸贴图的边缘还是圆的,阴影也没有改变。位移贴图效果更好,但要求模型本身顶点较多
- 本质上要求模型的变化要跟得上纹理的采样率

往往不想让模型太细致,因此 DirectX 使用 Dynamic Tessellation(动态曲面细分):开始先用粗糙的模型,在应用位移贴图过程中进行检测,如果需要,再将三角形拆开成很多小三角形,再继续做位移贴图
应用三:3D Procedual Noise + Solid Modeling
3D的纹理定义空间中任何一个点的值
- 除了2D纹理,还可以定义3D的纹理,定义空间中任何一个点的值。也可以不直接给出值而是定义一个3D空间的噪声函数,计算出空间中任意一点的值
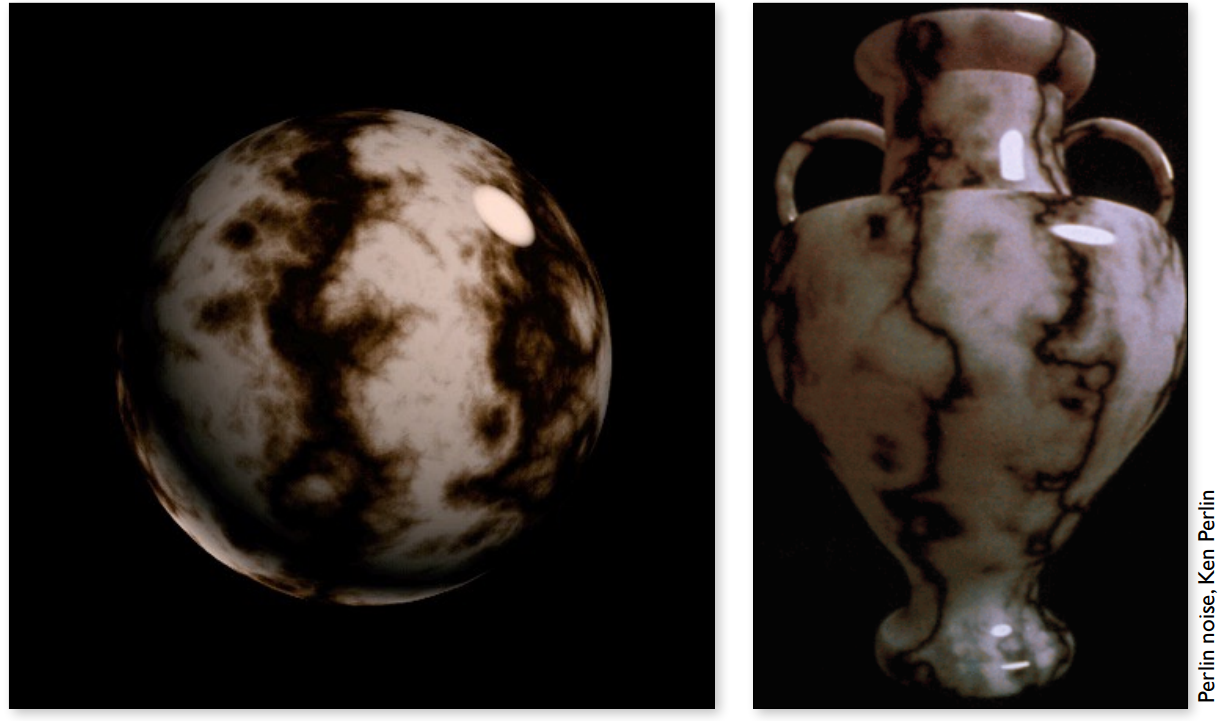
- 特别地,图中是 Perlin noise 噪声函数定义的裂缝图案,这个函数也可以定义山脉的起伏等,得到了广泛的应用。
- 3D Textures and Volume Rendering:3D纹理,被广泛应用到体积渲染里。比如得出每个点的密度
应用四:Provide Precomputed Shading
纹理记录之前算好的信息
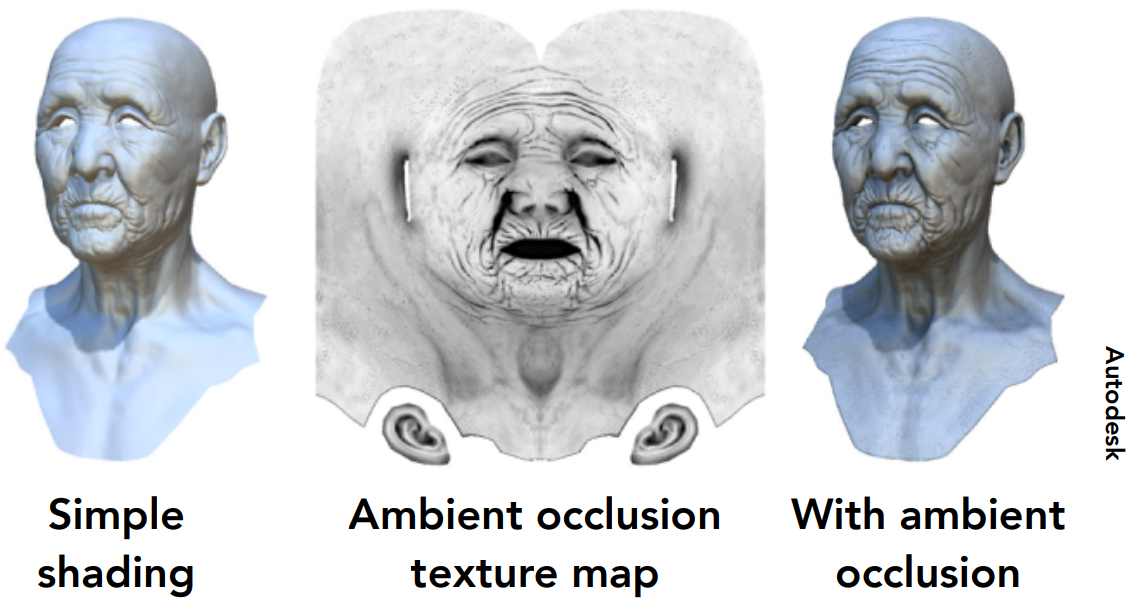
- 图中,右图眉毛遮挡一部分眼圈、投影阴影过来。在计算Shading时是不考虑这类信息的。
- 实时的做法叫 Ambient occlusion(环境光遮蔽),后面说
- 也可以事先计算好、写进一张纹理图(可见1、不可见0)、再把纹理贴上(着色结果跟纹理相乘)
+ 关于 Shading 的回顾
- Shading 1 & 2
- Blinn-Phong reflectance model
- Shading models / frequencies
- Graphics Pipeline
- Texture mapping
- Shading 3
- Barycentric coordinates,三角形内的插值
- Texture antialiasing (MipMap),纹理太大做范围查询
- Applications of textures
- 我的理解:重心坐标做三角形内的插值是在物体上,或者fragment(光栅化后)上的;而双线性、三线性插值是在纹理上的,主要解决纹理跟像素采样区域大小不匹配的问题。
到此,已经讲完了除了阴影技术外的光栅化过程,即硬件在做什么、实时渲染编程在做什么。
在实时渲染中,如何生成阴影、如何做近似的全局光照,等比较高级的内容,在之后的光线追踪中再说。
Lecture 10 - Geometry 1 (Introduction)
1 - 几何的表示方法
几何的显式、隐式表达
几何是非常复杂的。在图形学中进行如下分类,用不同的方式来表示不同的几何
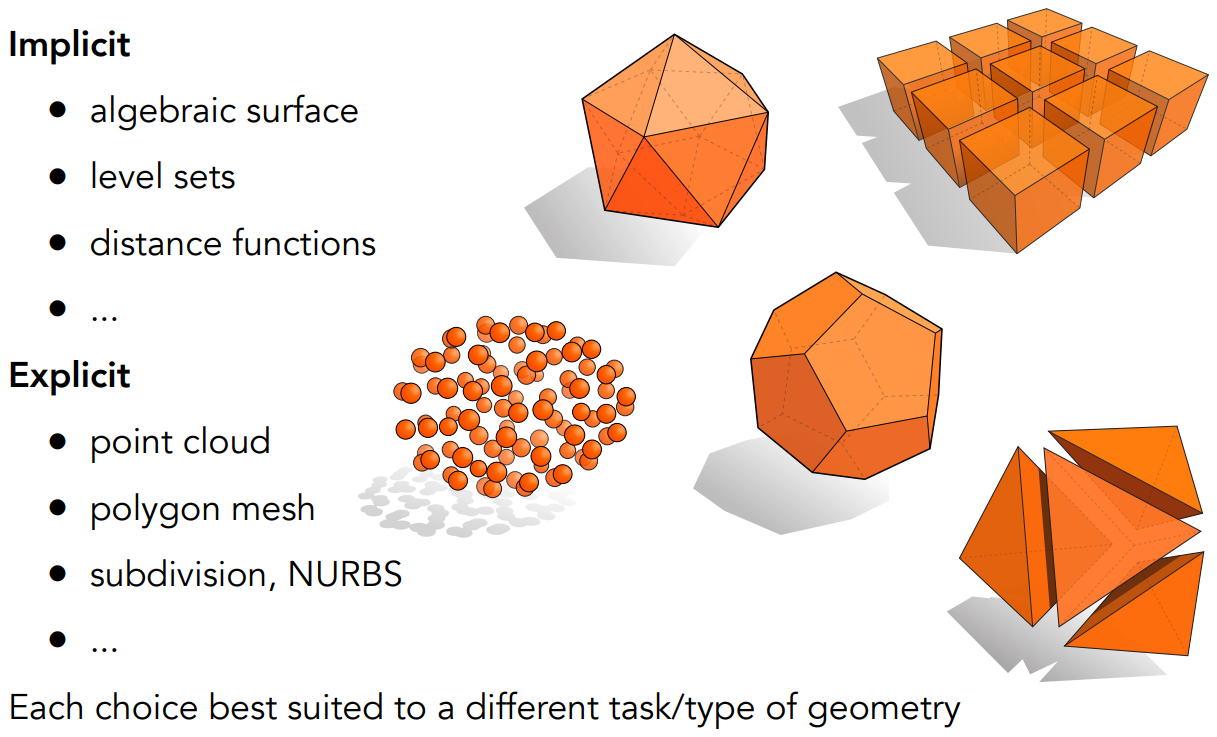
Implicit(隐式几何)
- 不给出点具体的坐标,只给出点满足的特定关系
- 广义来说,可以是 $f(x, y, z)=0$

- 对于隐式表示,得知有哪些点在图形内(Sampling,或者得知式子描述的图形长什么样子)是困难的;判断一个点是否在内部是简单的
- Sampling can be hard, but Inside/Outside Tests are easy.
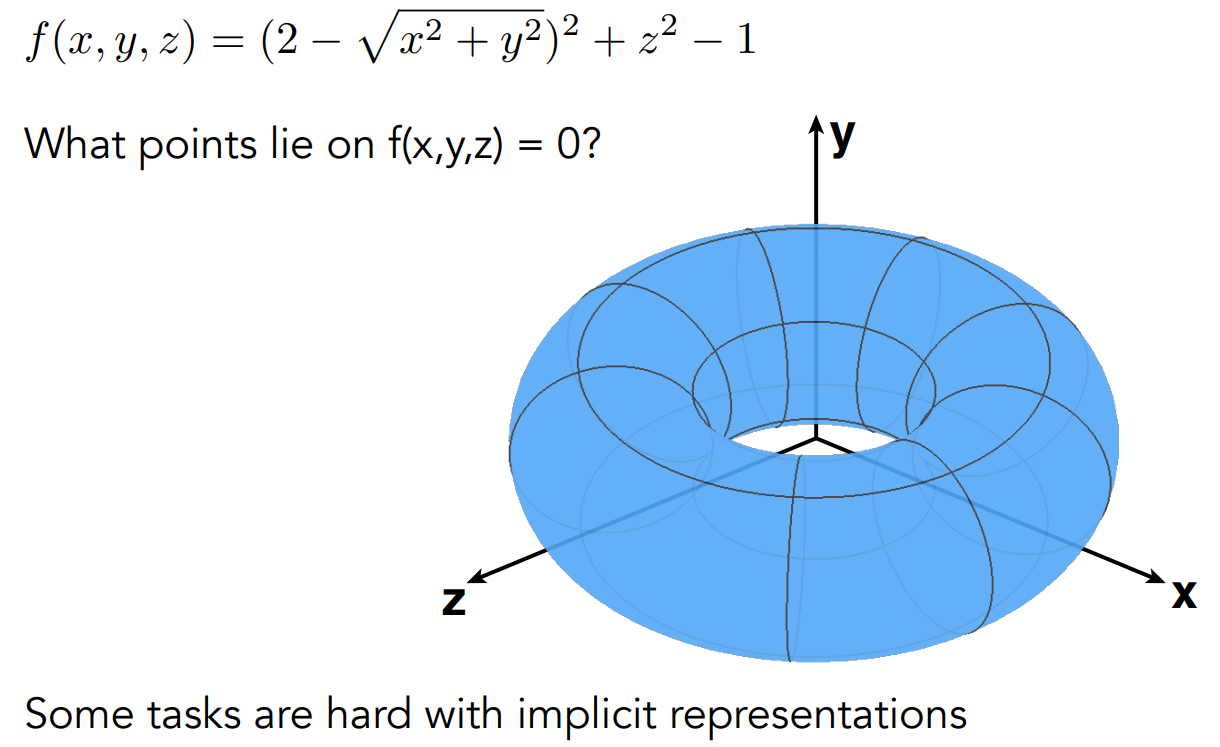
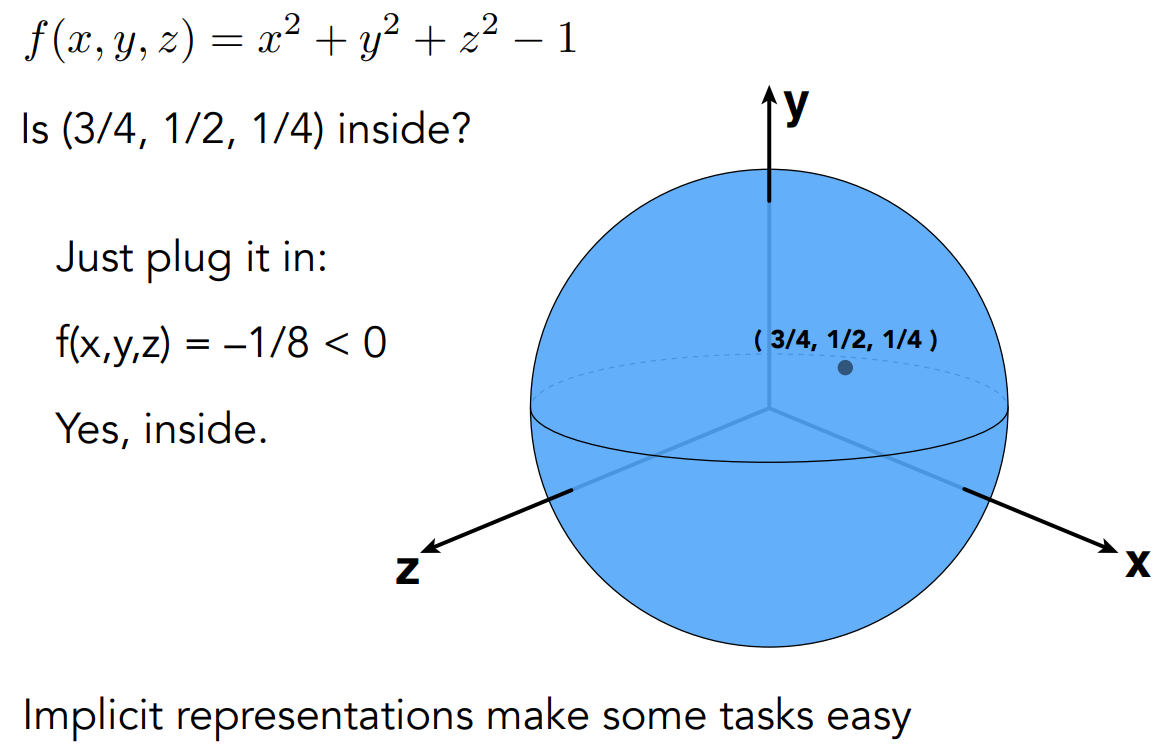
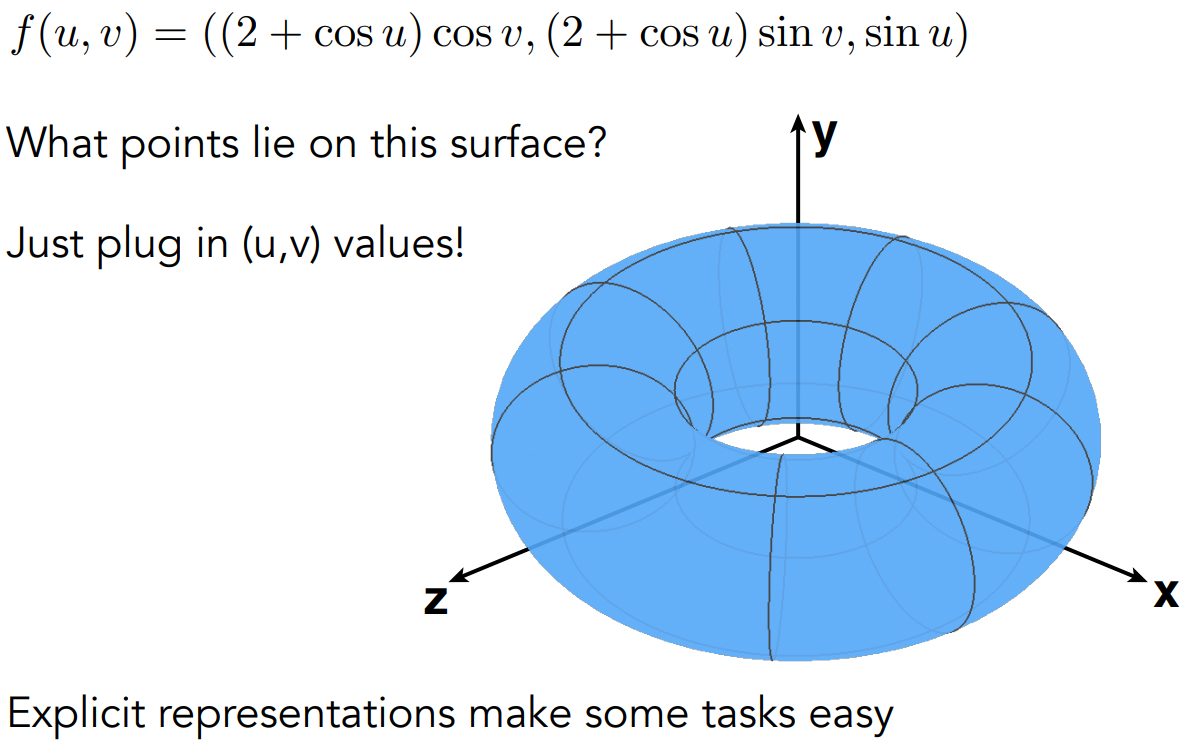
Explicit(显式几何)
- 直接给定所有的点,或通过参数映射的方法(如给定 $(u,v)$ 和对应到 $(x,y,z)$ 的方法)
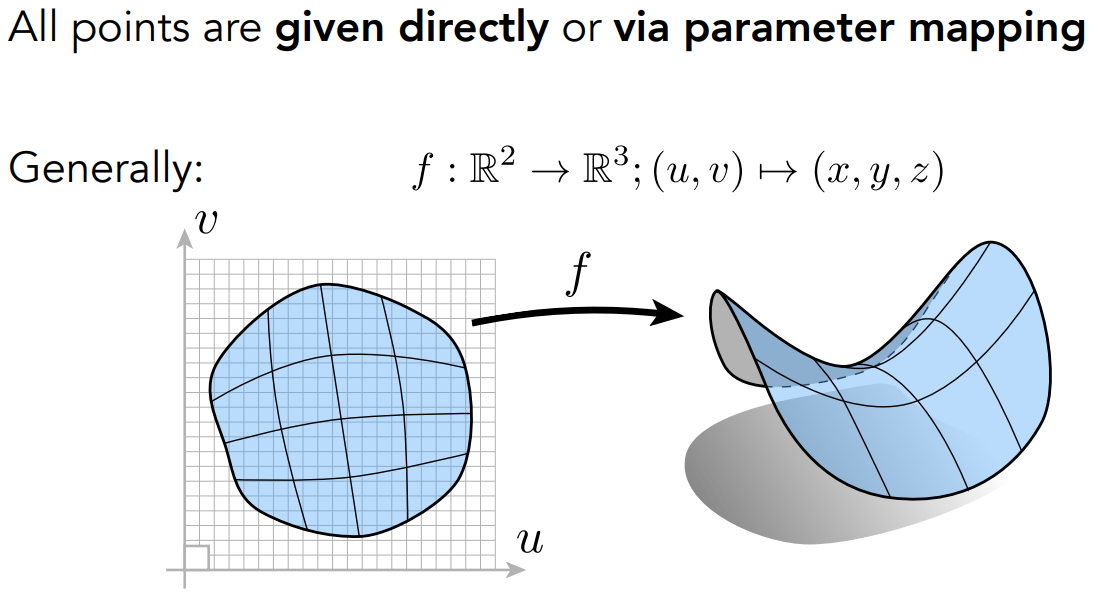
- 得知所有的点、显示几何形状是简单的;判断一个点是否在内、外是困难的
- Sampling is easy, but Inside/Outside Test is hard.
-

到目前,没有好的办法能完全解决几何的问题,需要根据需要去选择表示方法。
2 - 几何的隐式表达
更多的隐式表达方法
Algebraic Surfaces:直接用式子来表示
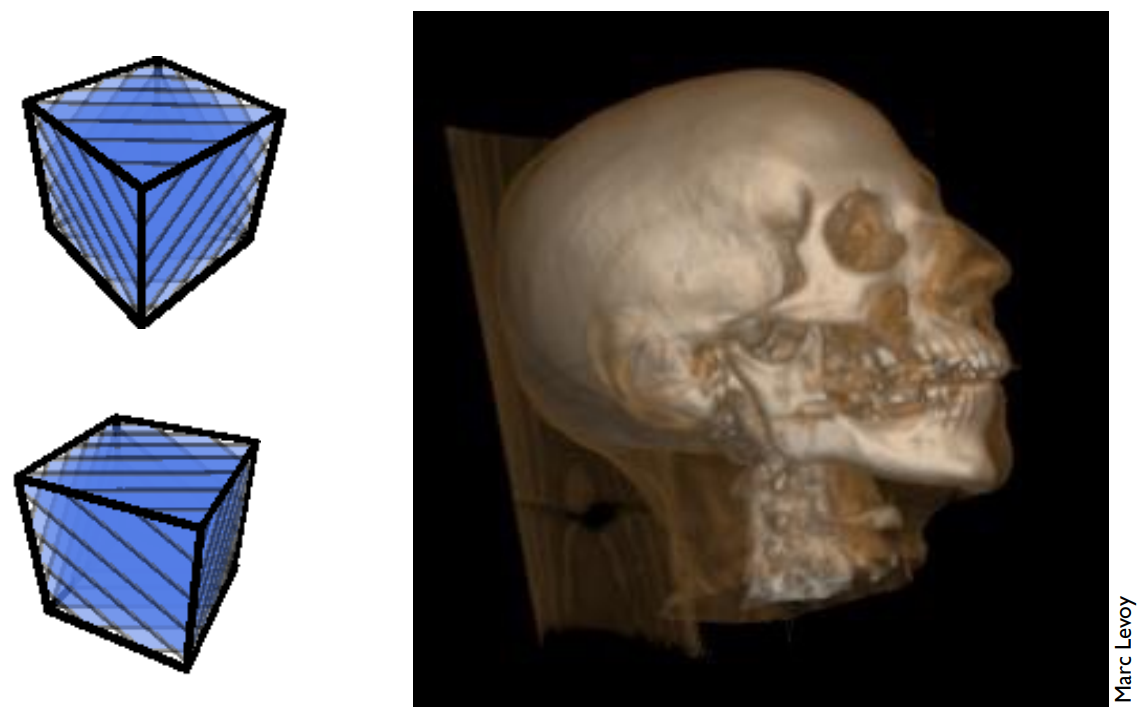
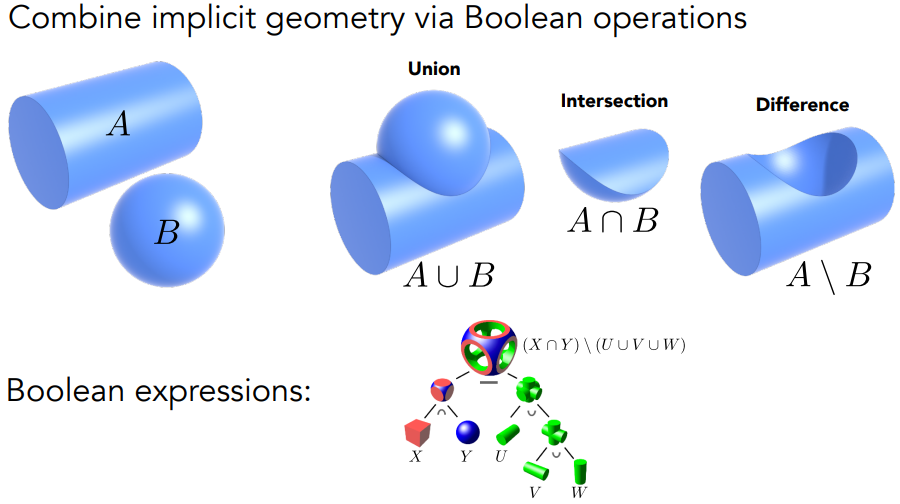
Constructive Solid Geometry:通过简单几何的布尔关系,表示更复杂的几何。已被广泛应用在建模软件中
Distance Functions:不直接描述几何,而存储空间中任意一个点到想要描述的几何的最小距离。如果点在物体内部,距离就是负的
- Signed DF,可以对距离函数做blending,也就是对物体表面做blending
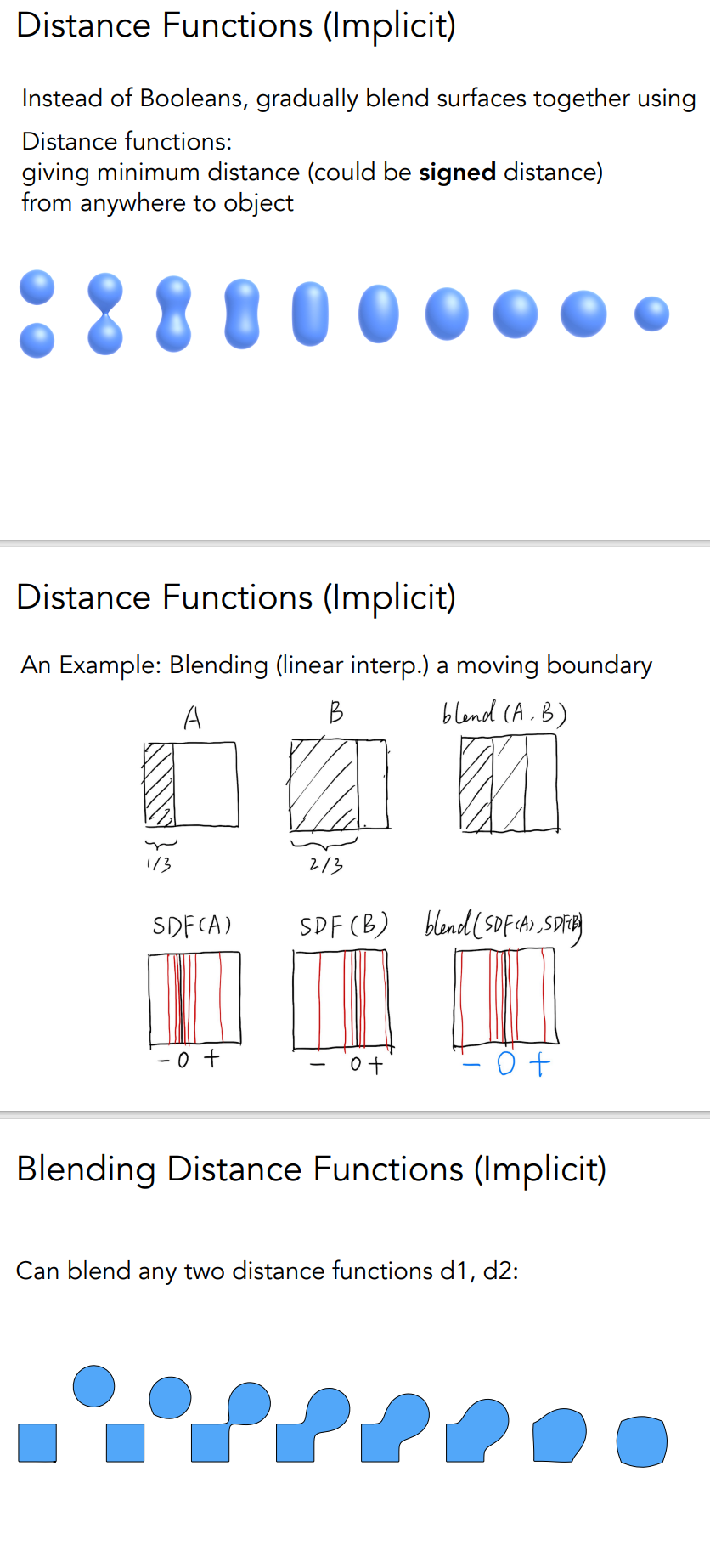
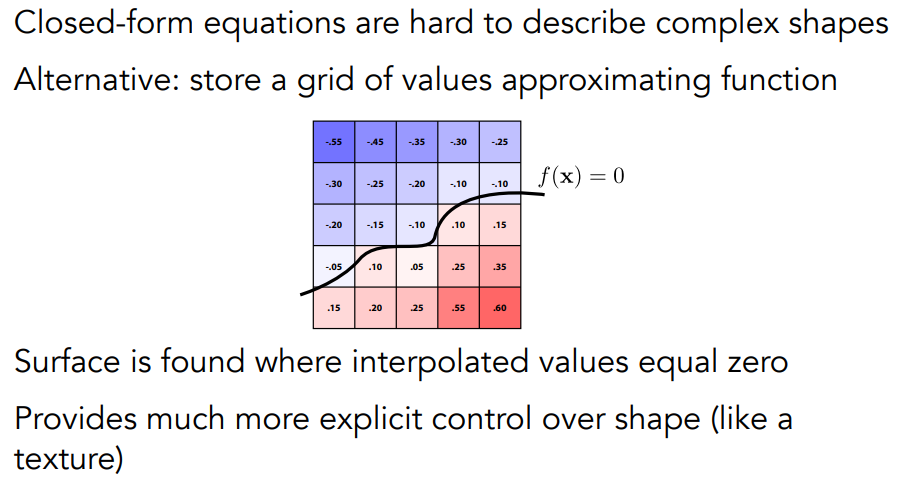
Level Set 水平集:也是距离函数的想法,只是直接把函数的值写在格子上
- 在医学数据(CT,MRI等)、物理模拟等使用,See http://physbam.stanford.edu
Fractals 分型:跟递归的概念相似
隐式几何表达方法的特点
- 优点
- 表述起来容易,存储方便。比如只用一个函数,或一个关系
- 内外查询、到表面距离查询方便
- 用隐式表示的表面,容易跟光线求交(直线跟平面公式求交)
- 严格描述物体
- 容易描述拓扑结构,如流体
- 缺点
- 难以用函数描述复杂的几何,如奶牛
3 - 几何的显式表达
更多的显式几何表达方法
- Point Cloud 点云:list of points $(x, y, z)$
- 很简单的表示方法,但有一些局限性,用得不多
- 扫描出的一堆原始数据就是点云

- Polygon Mesh 多边形面:用三角形(多边形)描述复杂物体
- 是最广泛应用的方法

- 下图是真实工程中的一个立方体。分别是8个点(v),6种法线(vn),12个点的纹理坐标(vt),各个顶点形成的三角形(f,顶点v/纹理坐标vt/法线vn)
- 数字对不上是因为自动生成,发生冗余
- 如,36行是一个三角形:使用5、1、4顶点,1、2、3纹理坐标,1、1、1法线

- 以上是几个不同的例子。在图形学中,从曲线开始,定义各种曲线曲面,来定义显式几何。作为下节课的开始
Lecture 11 - Geometry 2 (Curves and Surfaces)
- Curves: Bezier curves, De Casteljau’s algorithm, B-splines etc
- Surfaces: Bezier surfaces, Subdivision surfaces (triangles & quads)
贝塞尔曲线给出了每个点的计算方法,是显式的几何表示方法
1 - Bézier curve 贝塞尔曲线
定义
用一系列控制点定义某个曲线。定义一个入方向、一个出方向,可以确定一条曲线
定义任意多的控制点,如何画出一条贝塞尔曲线?
计算方法:de Casteljau’s Algorithm
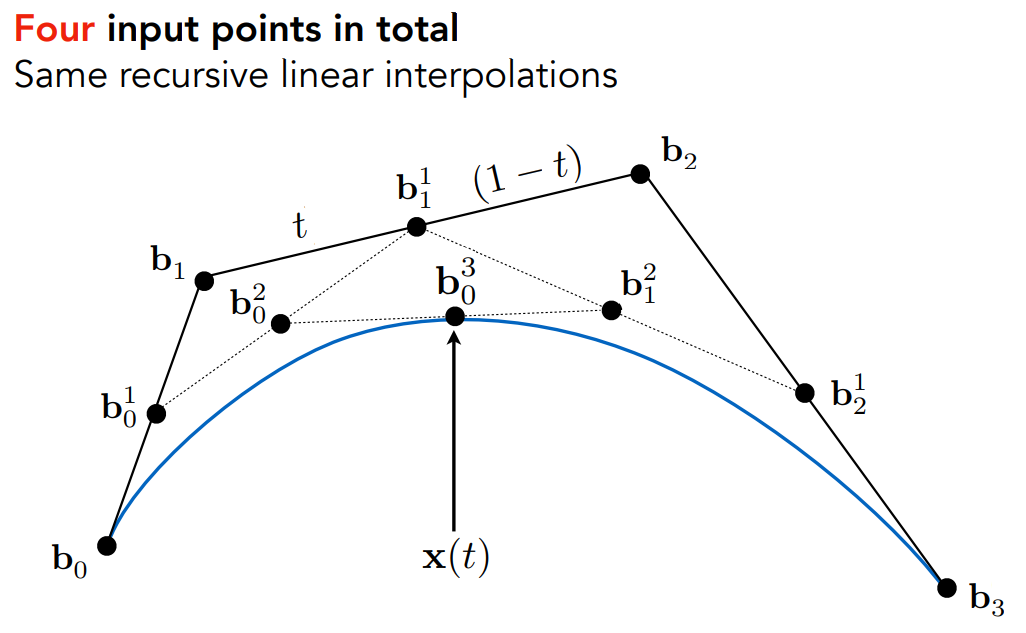
- 以四个控制点为例。定义一条曲线的起点在时间0,终点在时间1
- 任意一个时间 t
- 根据它在线段 $b_0b_1$ 的相对位置,找到对应在 $b_1b_2,b_2b_3$ 的点,将它们相连
- 四个点、三条线段,变为了三个点、两条线段 $b_0^1b_1^1, b_1^1b_2^1$ 。每次会少一个点
- 递归在每个线段上找 t 对应的位置,直到只剩一个点
- 这个点就是时间 t 对应在贝塞尔曲线上的位置
- 取一系列 t,最终得到完整的曲线
显式几何要么是直接给出点,要么是给出参数化的点计算方法。贝塞尔曲线作为显式几何表示方法,就是给出了每个点的计算方法。
贝塞尔曲线的代数表示
从计算过程推导
下图金字塔里左右边乘的系数写反了
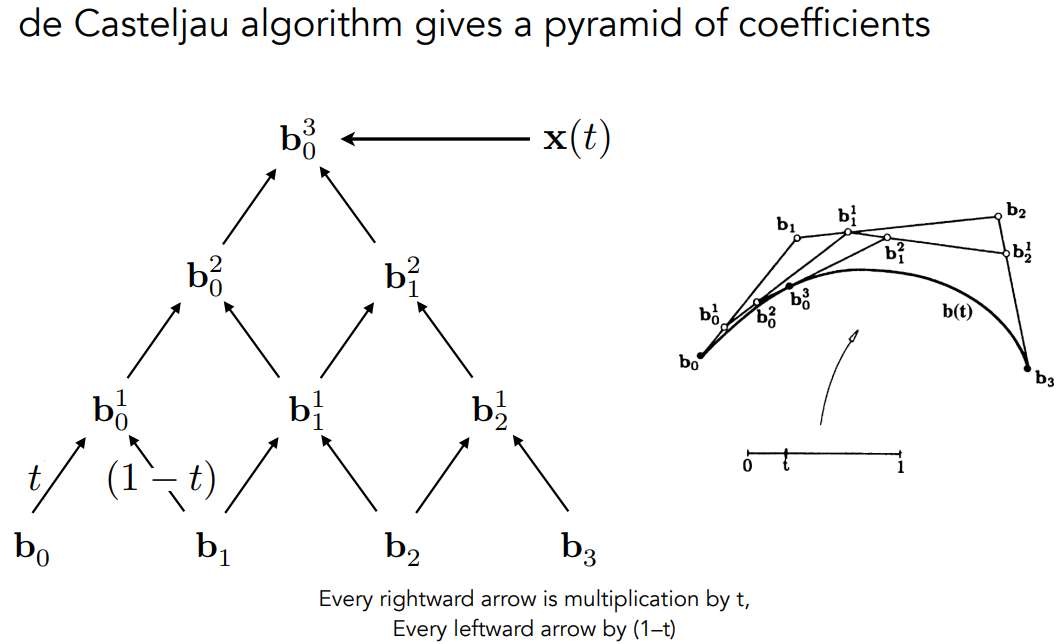
以三个点的二次贝塞尔(quadratic bezier)为例:

代数定义
- 给定 n 个控制点,就可以得到 n 阶贝塞尔曲线
- 任意 n 阶数的贝塞尔曲线,上面的时间 t,对应位置由伯恩斯坦多项式作为系数,对给定的控制点的加权
- $\bold b^n(t)=\bold b^n_0(t)=\sum^{n}_{j=0}\bold b_jB^n_j(t)$
- $B^n_i(t)=\begin{pmatrix}n\\i\end{pmatrix}t^i(1-t)^{n-i}$
- 对于3D空间的控制点,一样可以进行伯恩斯坦多项式的计算
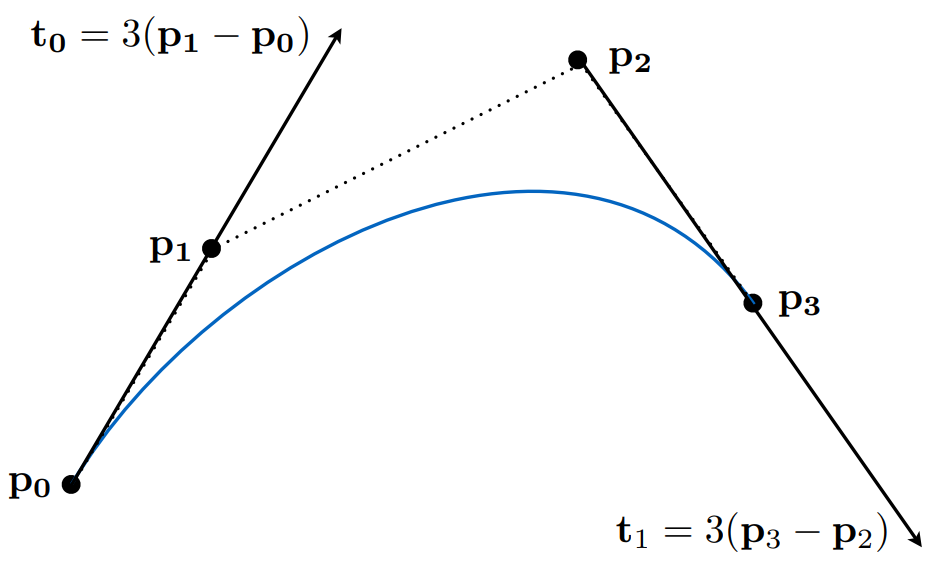
贝塞尔曲线的性质
- 规定必须过起点和终点,两个点处切线的方向可以通过一阶展开式来算。如果4个控制点,系数就是3
- 仿射变换不变性
- 可以先对控制点做仿射变换、再计算贝塞尔曲线,不必记录贝塞尔曲线的若干点、做仿射变换
- 对于投影变换就不行。投影变换不是仿射变换(平移不是仿射变换,透视投影中 $M_{persp\rightarrow ortho}$ 的最后一行也不是齐次坐标的 $(0,0,0,1)$ )
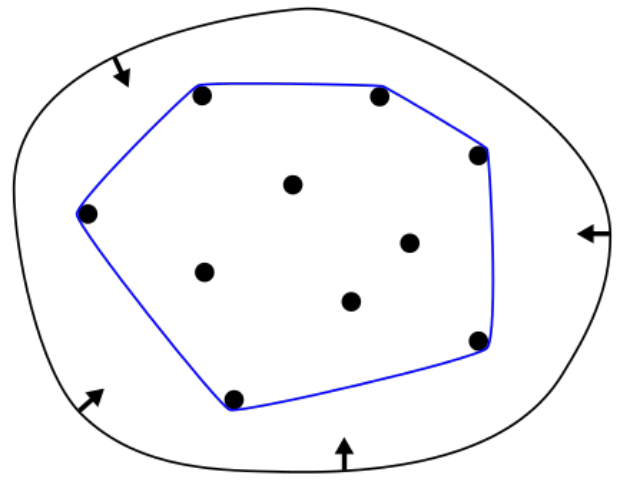
- 凸包性
- 最终的贝塞尔曲线一定在所有控制点形成的凸包内
- 凸包:包围所有点的最小凸多边形,图中的蓝色区域
- 由此,如果所有控制点排列在一条线上,贝塞尔曲线肯定就是直线
Piecewise Bézier curve 逐段的贝塞尔曲线
- 不使用很多控制点,定义一个贝塞尔曲线;而是每次用很少的控制点,定义贝塞尔曲线的一段,最后再连起来
- 通常,大家喜欢定义 Piecewise cubic Bézier(四个控制点、三个线段的贝塞尔曲线),分别是开头、结尾端点 + 两个控制点
- 如果希望不同段之间平滑连接,由之前的第一个性质,开头、结尾处的切线方向就是两个控制点之间的方向。因此把对应的三个控制点放到一条直线上就行
- 可以在这里试一下

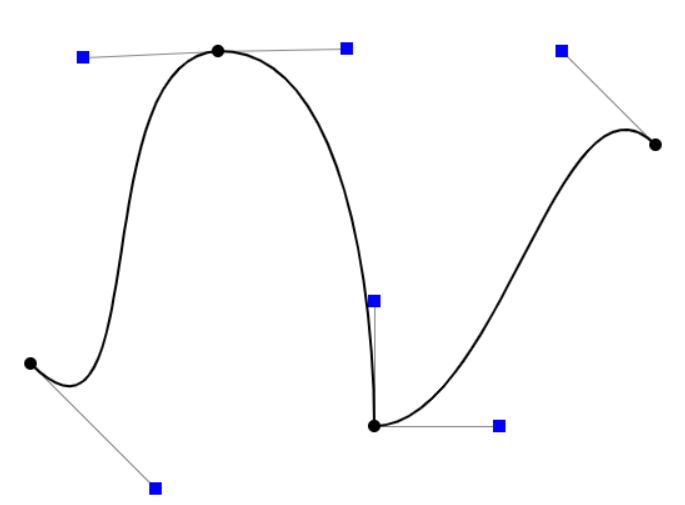
- 两段贝塞尔曲线的“连续”衔接
- $C^0$ 连续:在几何上都过同一点。两个函数在值上连续
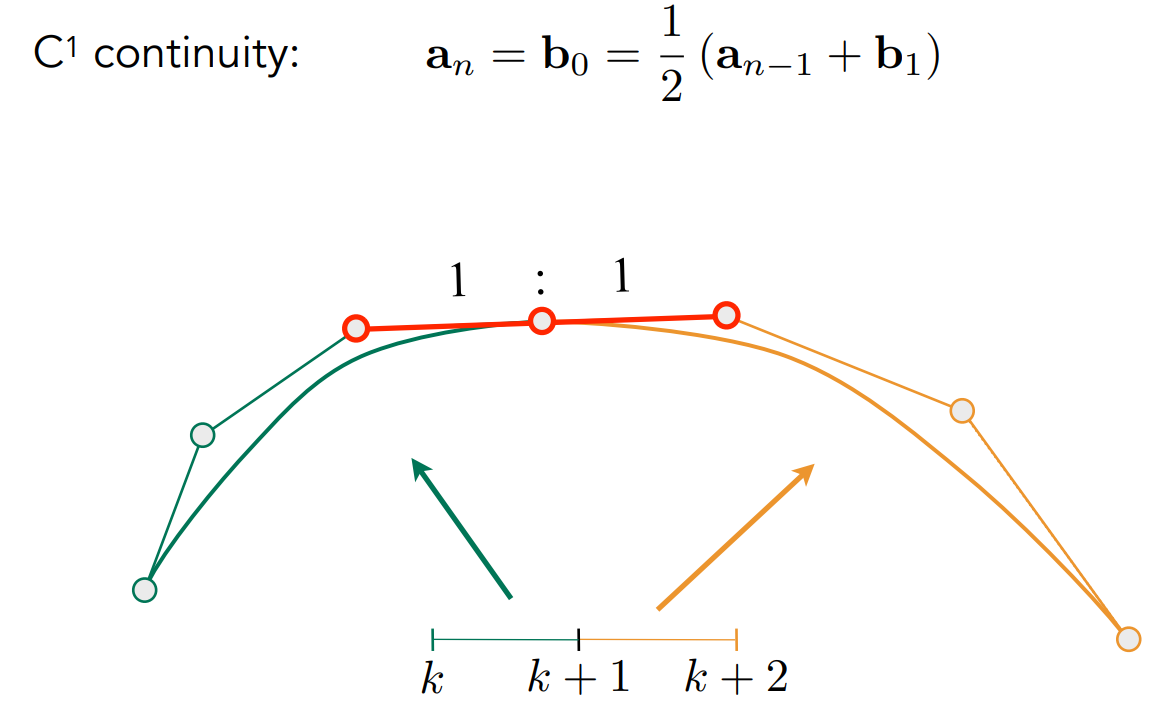
- $C^1$ 连续:在过同一点的基础上,共线、方向相反、距离相同。理解为一阶导连续
- 也有更高阶的连续,要求曲率连续等
- $C^0$ 连续:在几何上都过同一点。两个函数在值上连续
图形学中的贝塞尔曲线
- 除了贝塞尔曲线,图形学中也用其他方式定义曲线
- splines(样条):定义曲线经过的一些点
- B-splines:贝塞尔曲线的扩展
- 贝塞尔曲线动一个点、整个线会改变,只能通过分段来避免这个缺点。而 B-splines 有更好的局部性
- B-splines 是极其复杂的,还有 NURBS 等延申。本课只讲到贝塞尔曲线
2 - Bézier Surfaces
从贝塞尔曲线可以得到贝塞尔曲面。
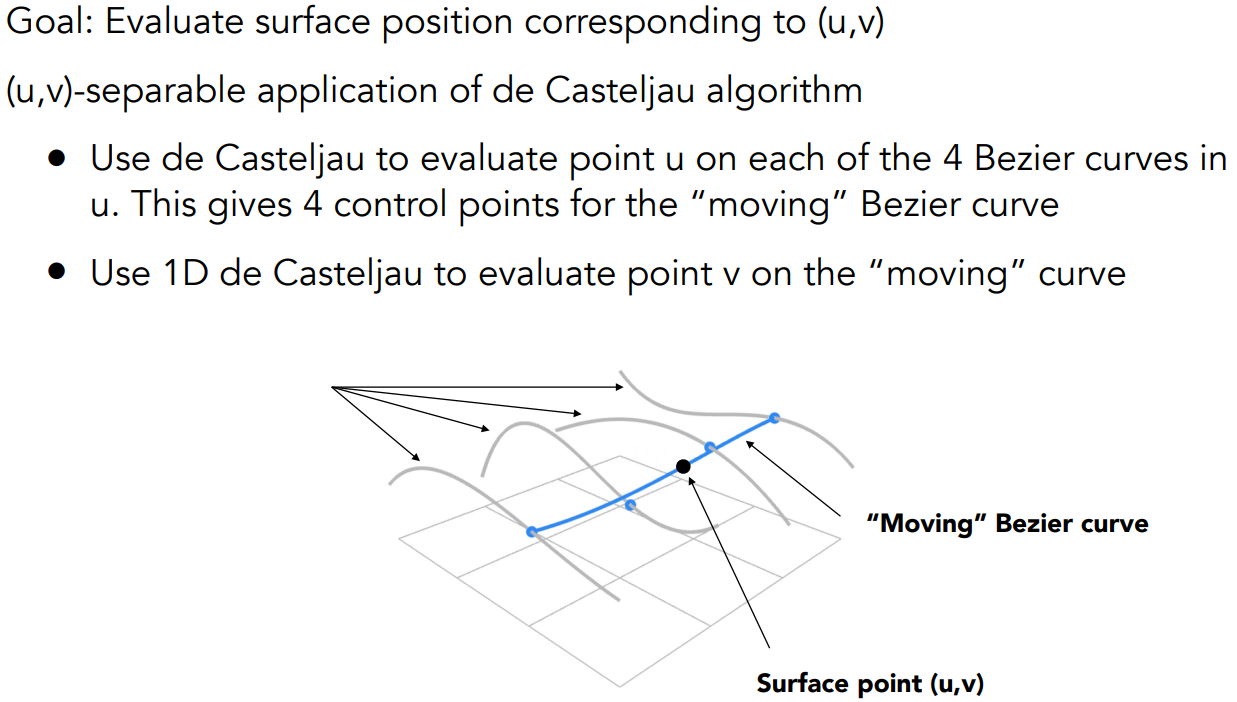
使用双线性插值的思路:在两个方向上,分别应用贝塞尔曲线
- 以 4×4 为例,在 4 行上应用贝塞尔曲线,每个时间都会得到对应的 4 个贝塞尔曲线的点
- 把这 4 个点作为另一个方向上的贝塞尔曲线的控制点,最终画出曲面
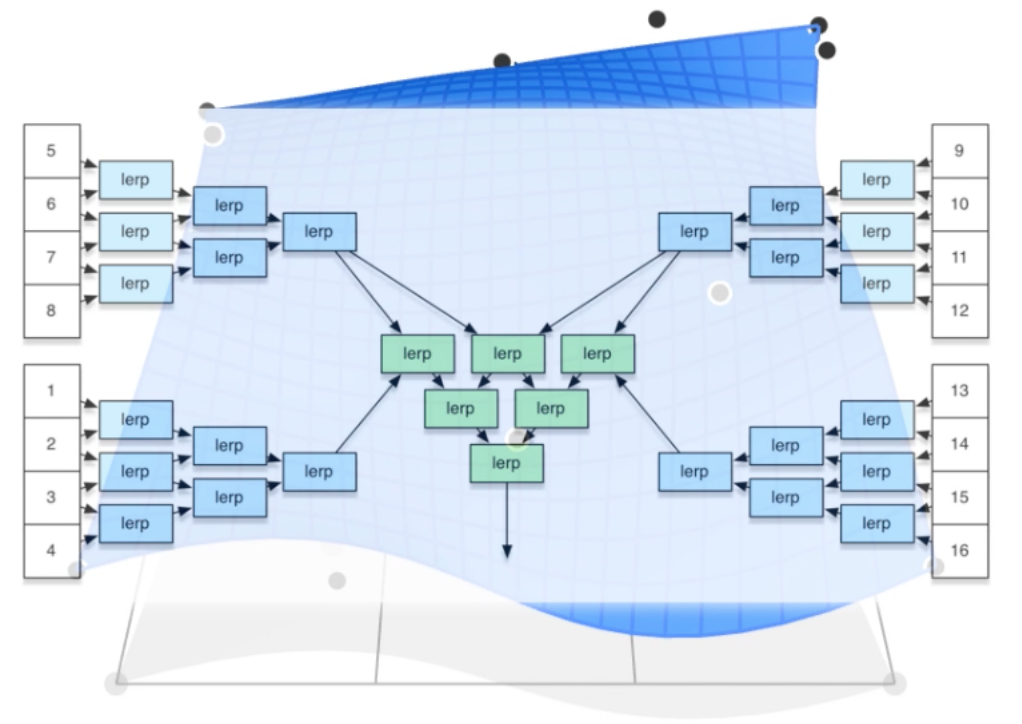
在此过程中,会有其他问题,比如怎样保证把每条贝塞尔曲线拼到一起后,还能形成连续的曲面。往往是通过两个时间尺度 $(u,v)$ 来统一进行参数映射
Lecture 12 - Geometry 3
几何处理(对于多边形网格),shadow mapping
1 - Mesh Operations: Geometry Processing
引入
Lecture 10 提到,用 Polygon Mesh(多边形网格)表示几何是目前最常用的方式。用三角形或四边形网格,描述不同的表面。是一种显式的几何表示方法。
对于Mesh,涉及到几种几何处理:
- Mesh subdivision 网格细分:使用更细致的网格,表示更平滑的曲面。upsampling
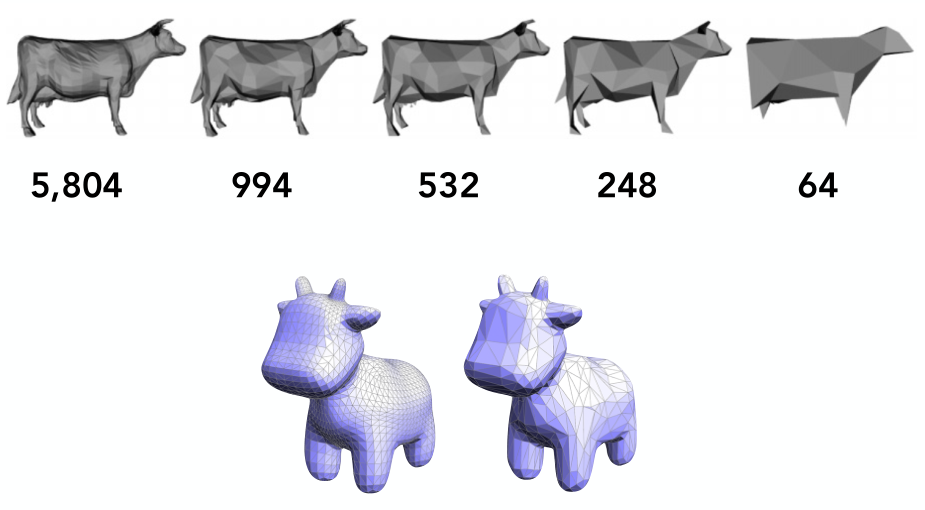
- Mesh simplification 网格简化:用更少的网格,节省存储(在保持基本形状的前提下)。downsampling
- Mesh regularization :避免出现特别尖 / 长的三角形,而是都跟正三角形类似。

Mesh Subdivision 网格细分(upsampling)
各种网格细分算法大致都分两步:首先往细节划分,然后改变位置。
Loop Subdivision
loop细分(发明人叫loop,跟循环没关系)分成两步:先细分、再调整。
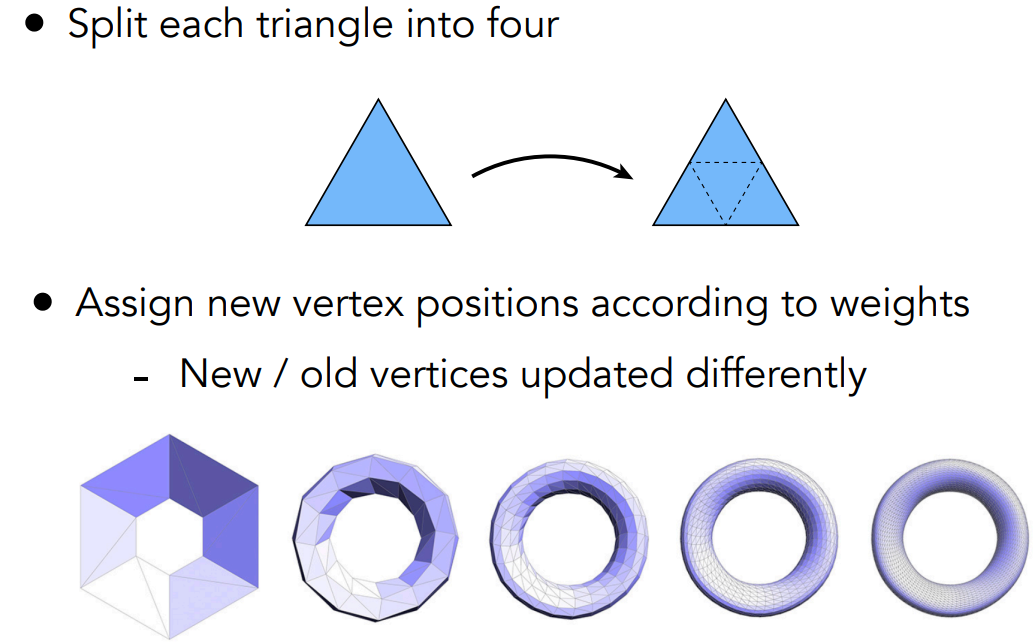
细分,增加三角形数量
- loop细分把一个三角形拆成四个
调整,改变三角形的位置
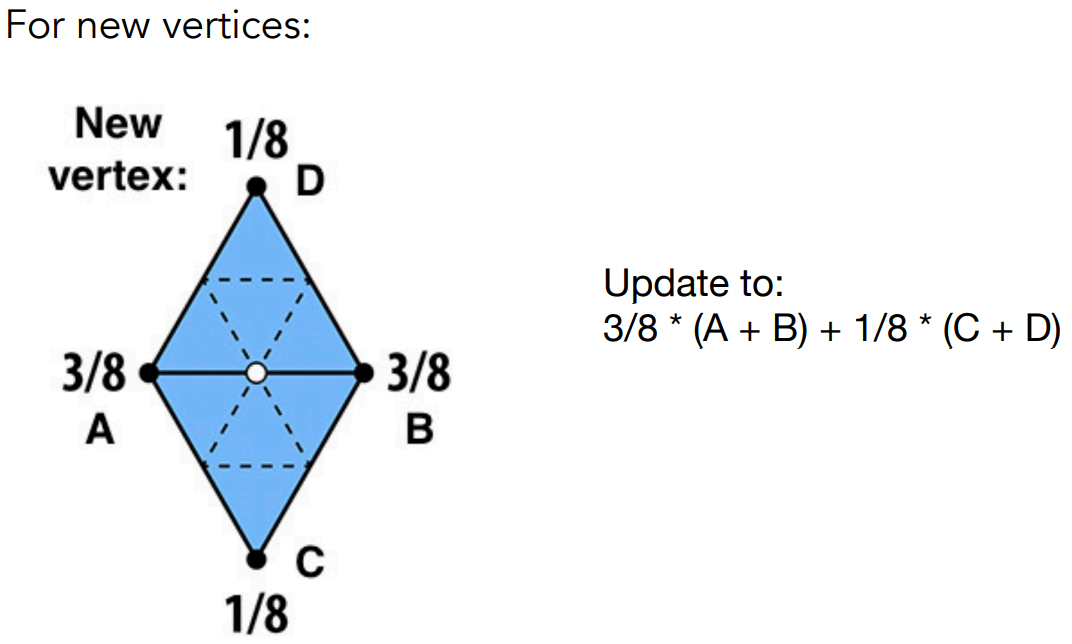
- loop细分把顶点分为 新、旧 两组。新顶点是各边的中点,旧顶点是三角形的顶点。使用不同的策略改变它们的位置
- 对于新顶点,考虑其相邻两个三角形,进行调整
- 对于旧顶点,一部分考虑相邻的6个旧顶点,另一部分保留自己的位置
Loop细分仅对三角形细分,不适用于一般场合
Catmull-Clark Subdivision
- 引入概念
- Non-quad face 非四边形面:不是四边形的面
- Extraordinary vertex 奇异点:度不为4的点
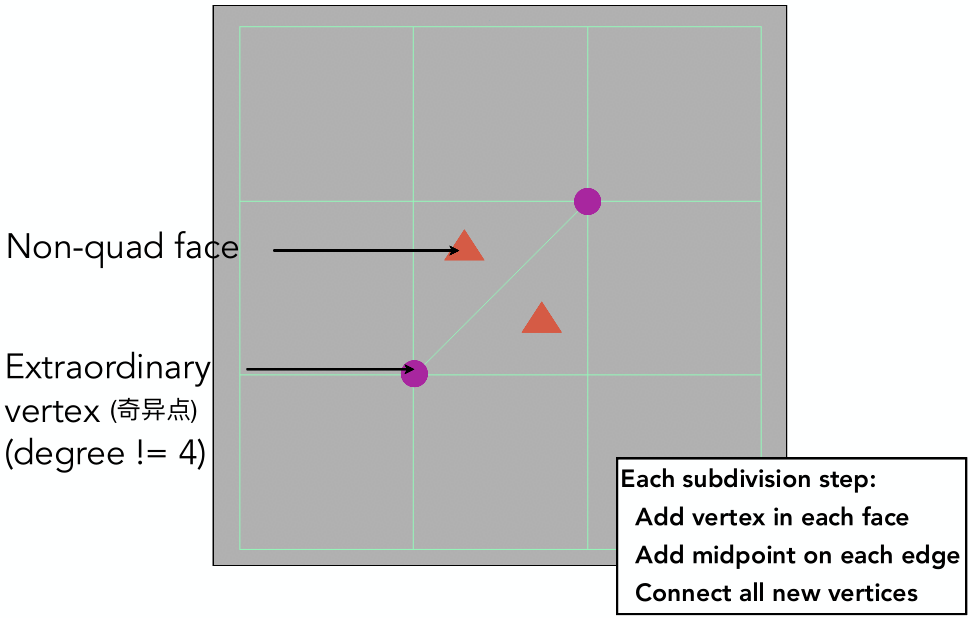
- 细分方法
- 非四边形面每条边取中点、每个面取中点,把它们连起来
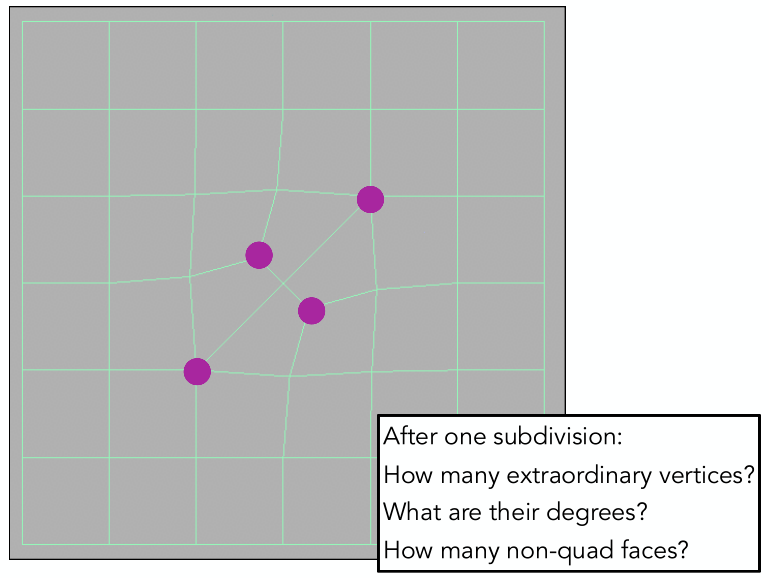
- 每一个非四边形面都引入一个新的奇异点;在引入奇异点后,非四边形面消失
- 宏观上的现象:每个非四边形面,在一次细分后,都变成一个奇异点 。在第一次细分之后,就不可能再有非四边形面了。
- 调整方法
- 依然是分为新点(再分边的中心点、面的中心点)、旧点(原来的顶点),分别做调整
- 无非就是定义规则、取平均,不再细说

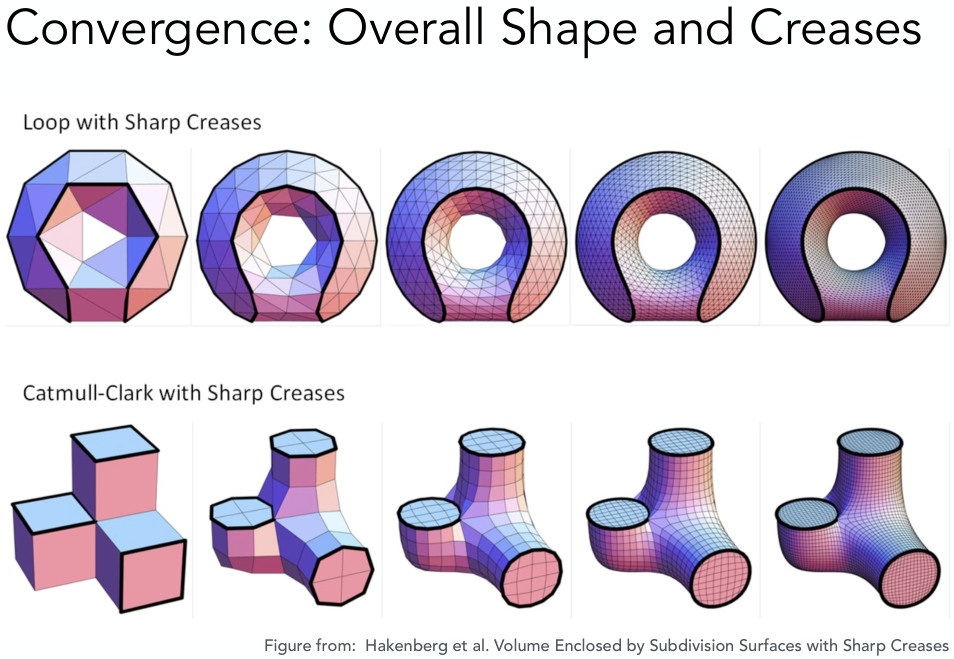
两种细分方法的效果
Mesh Simplification 网格简化(downsampling)
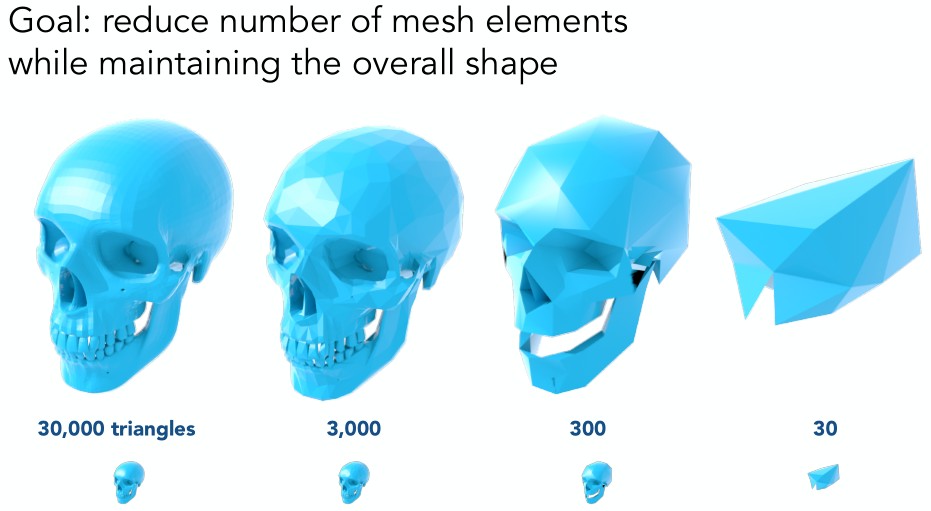
目的
出于计算资源的考虑,在不同的情况下会采用不同细分程度的模型。如离得远、在移动端,都常常使用低模。
高模和低模的几何模型,跟纹理的 MipMap 的概念类似,即“层次结构的几何”和“层次结构的图像”。然而,目前实现层次结构的几何是困难的,在存储、过渡(无法三线性插值)上都有不同的难题。
一种方法:Edge Collapse 边坍缩
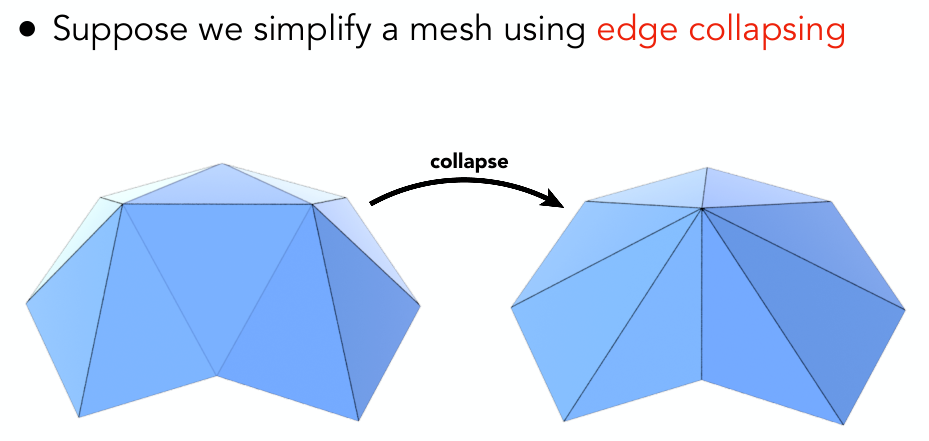
两个问题:如何判断在哪里进行坍缩,具体如何坍缩?
引入一种二次度量误差,我们希望把点放在新位置上,可以最小化二次误差
- 二次误差的概念跟 L2 距离相似,即让点到相关面的距离平方和最小

对于模型的所有边,都假设:如果坍缩这条边、并把点放在最佳位置上,会得到一个多大的二次度量误差
- 因此,对于一个模型,会从它的二次度量误差最小的边开始坍缩
- 对每条边打分,打的分就是二次度量误差。从小的开始、一个个进行坍缩
若干问题:
- 坍缩一条边后,会引起其他边的变化,二次度量误差也改变。因此,在一次坍缩后,需要更新关联边的二次度量误差
- 需要一个数据结构,能O(1)取最小值,并且以较小的代价更新受影响的元素——优先队列或堆
- 通过一步步执行局部最优解,试图达到全局最优解,属于贪心策略
- 坍缩一条边后,会引起其他边的变化,二次度量误差也改变。因此,在一次坍缩后,需要更新关联边的二次度量误差
使用边坍缩,简化的模型也能保留一部分特征
2 - Shadow Mapping
Shadow Mapping
动机
之前的着色(Blinn-Phong 反射模型),只考虑局部的现象:考虑 shading point 本身,考虑光源、摄像机。不考虑其他物体、或物体其他部分对着色点的影响。
实际上,其他物体挡住了 shading point,光线就到达不了,从而在 shading point 产生阴影。之前说的着色解决不了阴影,现在来解决这个问题——限制在光栅化内。
实现思路
Shadow Mapping 是图像空间的做法(Image-space algorithm)
- 在生成阴影的这一步,不需要知道场景的几何信息
- Shadow Mapping 本身会产生走样现象
关键现象:如果一个点不在阴影里,则(1)可以从摄像机看到这个点,(2)可以从光源看到这个点
Shadow Mapping 只能处理点光源、方向光源的阴影,这种阴影通常都有很明显的边界,一个点要么被看到、要么不被看到,也就是非0即1的判断过程,称为“硬阴影”
具体步骤
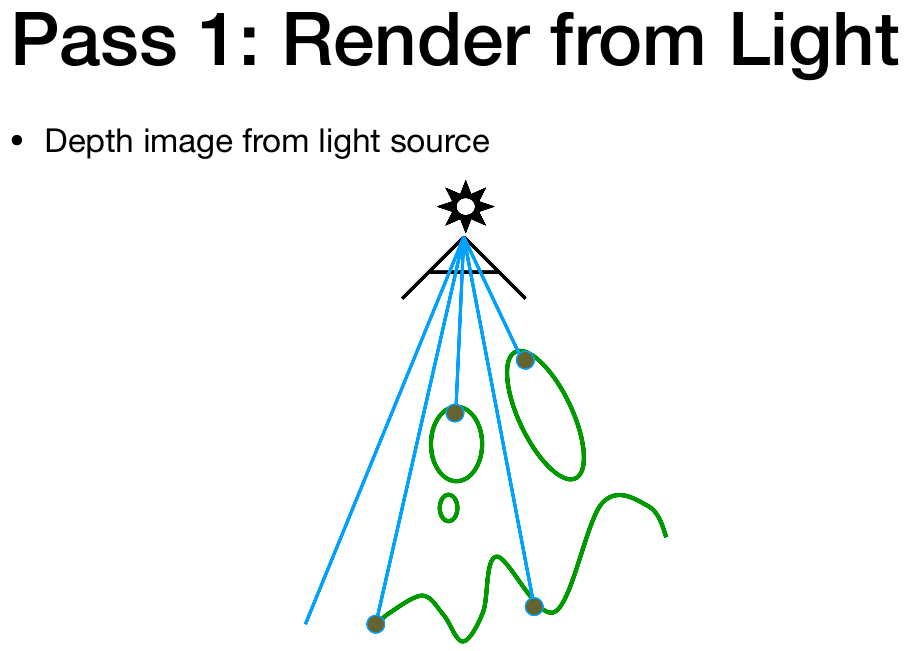
- 第一步:从光源渲染场景,记录不同方向看到的深度
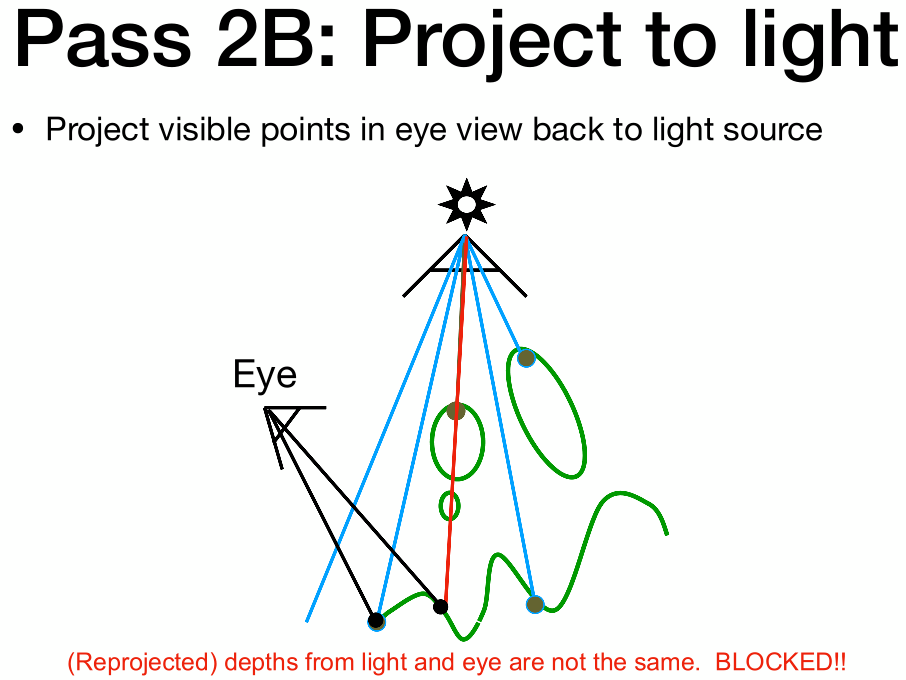
- 第二部:从摄像机渲染场景,看到的点投影回光源,检查光源图记录的该位置深度跟当前深度是否一致。如果不一致,说明被遮挡了
从实际渲染场合再次理解这两步:
- 从光源渲染场景,生成深度图
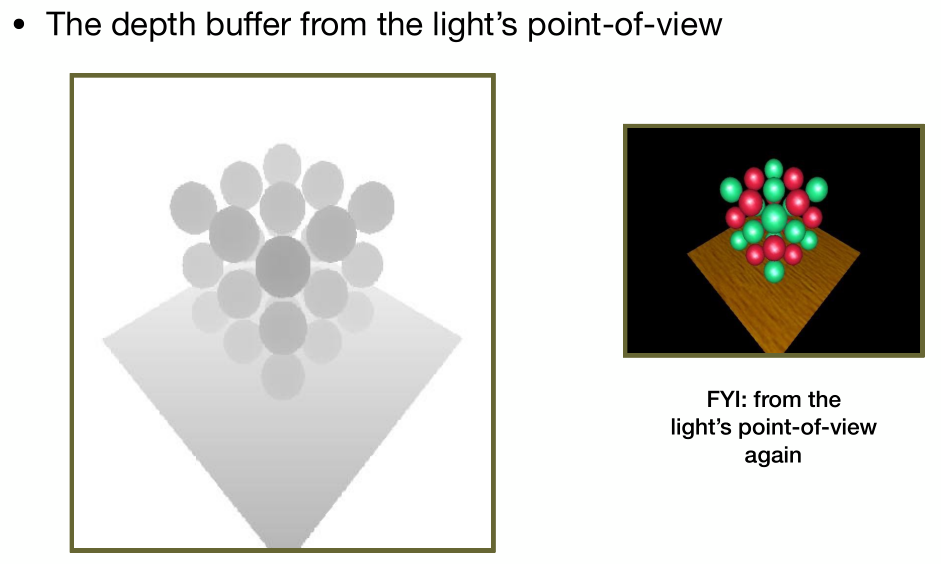
- 从摄像机渲染场景,每个点投影回光源,对比记录的深度跟当前深度是否相同

- 可以看到,图中有一些噪点出现,这是由于shadow mapping技术本身的一些问题
- 得到带有阴影的渲染结果
Shadow Mapping的若干问题
- 有浮点数判定相等的步骤,会带来数值精度问题
- 从光源看向场景的过程中,有不同的分辨率选择。如果 shadow map 的分辨率低、渲染场景的分辨率高,则记录的阴影信息是走样的。
- 之前提到,光栅化产生锯齿,如果用低分辨率的 shadow map,使用高分辨率渲染场景,那么高分辨率范围内的多个点投影到同一个深度像素上,就会产生有锯齿的阴影。如果用高分辨率的shadow map又会产生开销。
- shading 只做一次渲染(MVP变换、视口变换、光栅化),而 shadow mapping 需要渲染场景两遍(先从光源再从相机看向场景)
- 只能做硬阴影
然而,不妨碍 Shadow Mapping 技术成为主流的技术。也有不同的科研工作尝试解决上述三个问题。
硬阴影和软阴影
- 对于点光源,一个点要么可见、要么不可见,因此会形成边缘锐利的阴影,就是硬阴影
- 而软阴影指的是阴影会慢慢过渡,不再是非0即1。此外,越靠近物体根部,阴影越硬
- 软阴影是物理上的 Penumbra(半影)概念。物理上,一个区域完全看不到光源,就是全影,如果部分看到光源,就是半影
- 图中右侧是日食现象,有一部分位于本影区域,完全看不到太阳;有一部分位于半影区域,能看到一部分
- 因此,阴影的类型取决于能看到多少光源;点光源确实只能产生硬阴影;软阴影肯定不是由点光源形成的

本课程至此,已经讲完了图形学四大部分的前两个
- 光栅化:图形学的其他部分也会用到光栅化,因此首先讲。光栅化的着色,以及两次光栅化用 Shadow Mapping 做阴影都讲了
- 几何:显式隐式的表现方法,三角形面(几何处理,显式方法),曲线曲面(贝塞尔曲线,显式方法)等
- 光线追踪:不再用光栅化的方法继续做了,因为光栅化有一些现象不好做
- 动画 / 模拟
Lecture 13 - Ray Tracing 1 (Whitted-Style Ray Tracing)
为什么光线追踪,Whitted-style光线追踪,光线跟物体求交(隐式表面,三角形,AABB)
1 - Basic Ray-Tracing Algorithm
为什么光线追踪
光栅化的问题
光线追踪和光栅化是两个不同的成像方式。光栅化过程中,有一些问题没有解决好:
- 光栅化不好表示全局的效果
- (软)阴影
- Glossy反射、间接光照(光线在到达人眼之前弹射不止一次),等

- 光栅化的着色只考虑光线的一次弹射,从光源到 shading point、到人眼,如Blinn-Phong模型
- 光栅化的阴影使用 shadow mapping,不能处理软光照,生成软阴影
光栅化和光线追踪
- 把光栅化理解为:一种很快、很近似的渲染方法,质量相对低。可以用于实时场合。
- 光线追踪符合真实的物理规律,更准确,但更慢。更多作为离线的应用。(一帧要渲染10k CPU hour)
相关概念
图形学中的光线
在图形学计算中,通过简化现实生活中的光,给出光线的定义:
- 不考虑波。光线沿着直线传播
- 光线之间不会发生碰撞,交叉时不互相影响
- 光线从光源发出,最终进入人眼(打到场景中,经过反射、折射等)。光线追踪就是试图模拟这一过程
- reciprocity:光线的可逆性。人眼发出一些感知的光线,最后打到光源,仍然是一条可行的光路
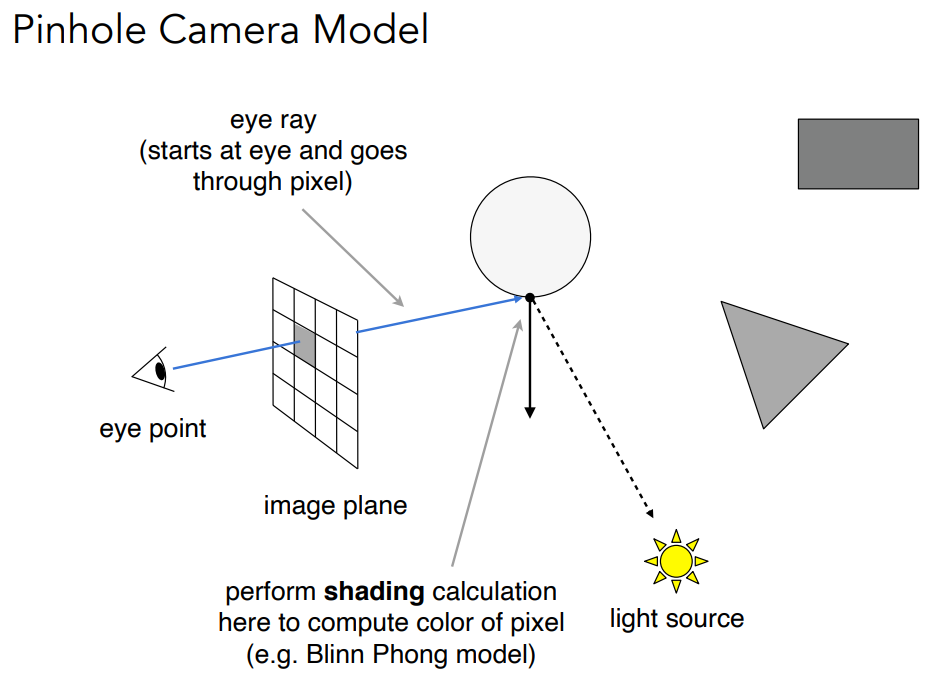
图形学中的Ray Casting
- 对于每个像素,从摄像机连一条光线、穿过像素格子、打到场景中的一个点
- 把这个点再跟光源连线,判断这个点对光源是否可见(是否在阴影里)
- 如果可见,就形成了一条有效的光路,可以计算能量并计算颜色(着色)
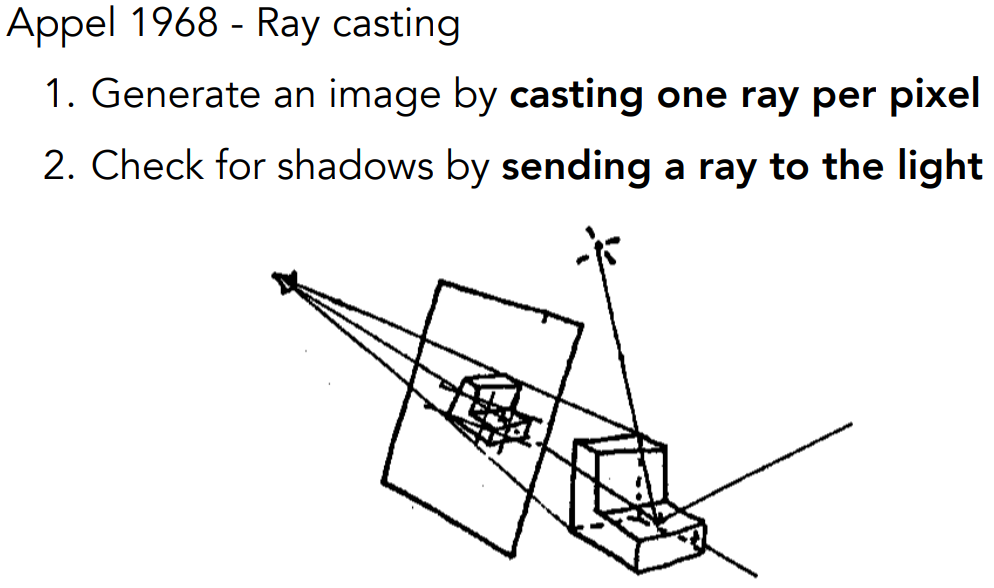
一个光线追踪例子
- 认为眼睛是一个针孔摄像机(一个点),光源是点光源,场景中的物体会发生完美的反射
- 光线从眼睛出发,经过每一个像素格子,投射到场景中,沿着一根光线记录最近的交点
- 在投射光线的过程中,也完美解决了深度测试的问题
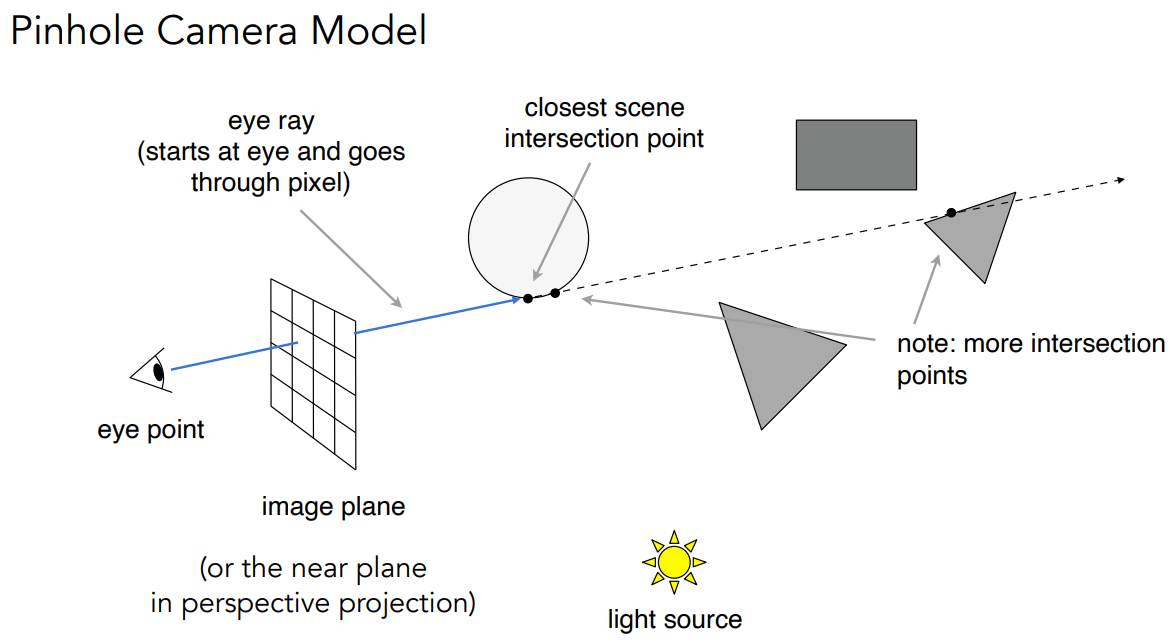
- 对于交点,检测会不会被光源照亮
- 交点向光源连一条线(shadow ray),如果中间没有物体阻挡,则光源可以照亮这个点,否则会被阴影阻挡
- 根据法线方向、入射方向、出射方向、光线,计算该点的着色情况,填入像素格子
到此,光线还是只弹射一次。如果想弹射很多次,则使用Whitted-Style光线追踪,它是一个递归的过程。
2 - Recursive(Whitted-Style) Ray Tracing
整体思路
whitted style 就是在模拟光线不断弹射的过程
- 光线会分成若干光路(镜面反射、折射),并且每条光路折射的次数多了
- 对每一个交点,都连接 shadow ray 判断光源可见性,分别做着色,计算颜色值
- 每折射一次,都会发生能量的递减
- 把每条光路所有点的着色加到像素的值里去
- 对不同的光线进行归类
- 从眼睛打出来的第一根光线,称为 primary ray
- 在一次弹射之后的光线,称为 secondary rays
- 从折射点往光源的连线,称为 shadow rays
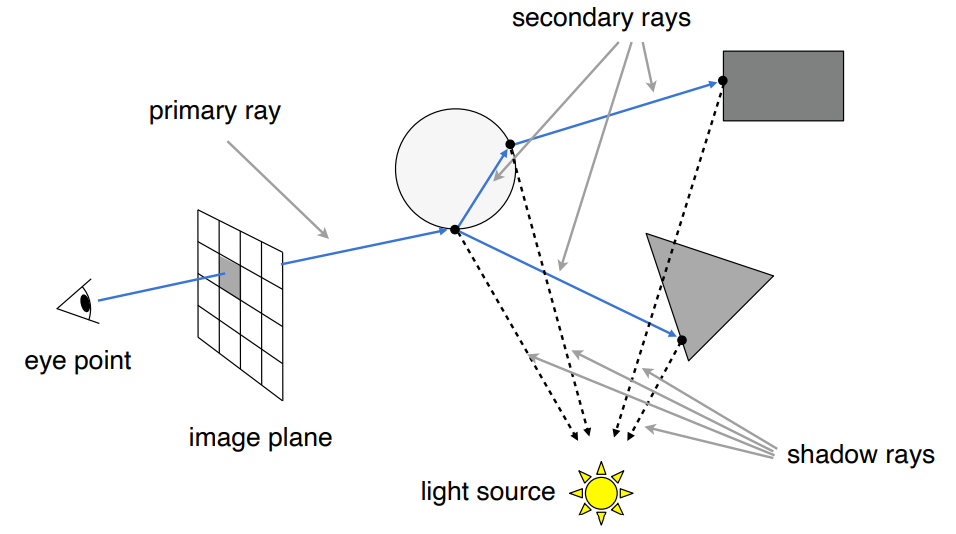
3 - Ray-Surface Intersection(如何求光线和场景内物体的交点)
光线
- 光线:起点和方向
- 是一条射线
- 起点 $\bold o$,方向 $\bold d$
- 光线上 $t$ 时刻的点表示为:$\bold r(t)=\bold o+t \bold d \space (0 \leq t \lt \infty )$
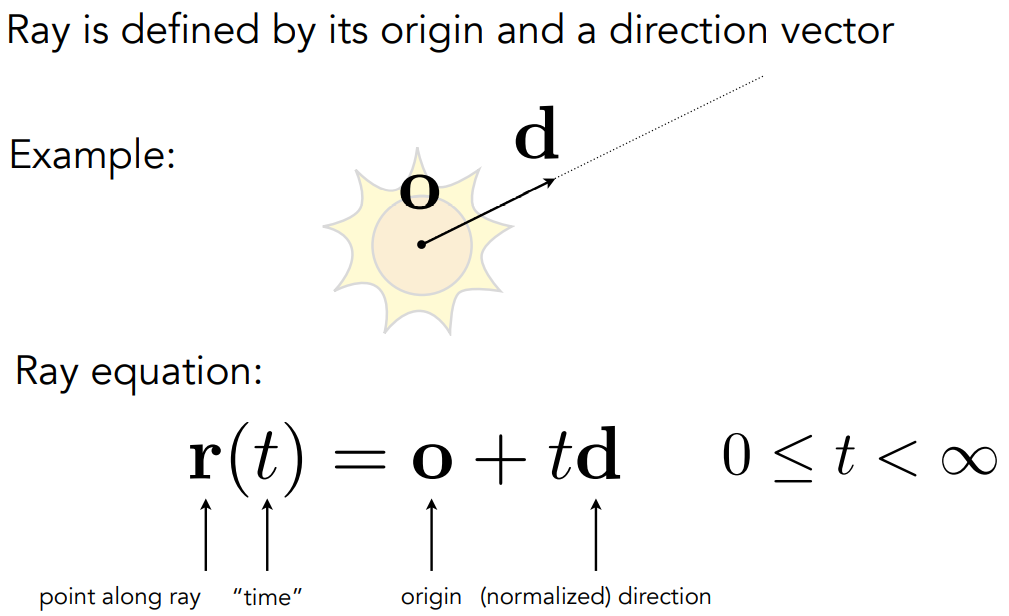
光线跟隐式表面求交
光线跟球求交:解二次函数
- 球:$\bold p:(\bold p-\bold c)^2-R^2=0$
- 交点意味着同时满足在球上、在方向上,因此将两个方程联立即可
- $(\bold o+t\bold d-\bold c)^2-R^2=0$
- 求解这个关于 $t$ 的二次方程即可,取非负数、非虚数的解

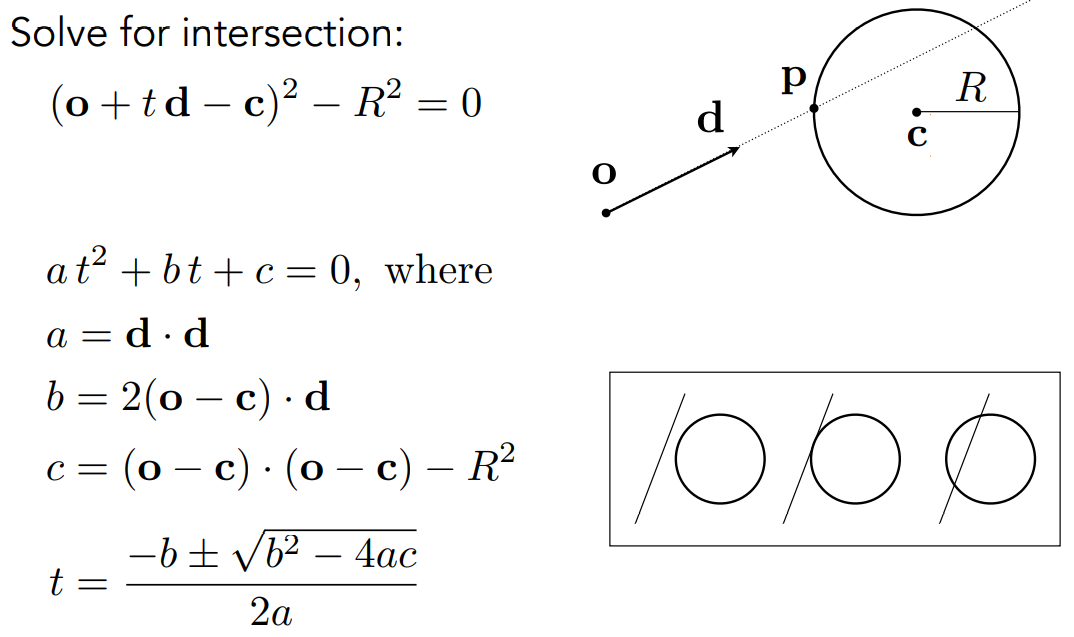
推广:光线跟任意隐式表面求交
- 隐式几何表面:$\bold p:f(\bold p)=0$
- 交点处 $f(\bold o+t\bold d)=0$
- 求解关于 $t$ 的方程,取非负数、非虚数的解,交点是 $\bold o+t\bold d$

光线跟显式表面求交之1——三角形
光线跟三角形求交
- 应用:
- Rendering: visibility, shadows, lighting …
- Geometry: inside/outside test
- 使用拓扑学定理:从一个封闭图形的内部发射射线,跟图形表面的交点数量一定是奇数
- 求光线跟显式几何的交点
- 朴素的思路:挨个判断光线跟物体表面的每一个三角形面是否相交,离光源最近的交点就是要求的交点
- 结果可能是0个交点或1个交点
- 计算量太大:每根光线要做 #pixels × #objects;如果光线折射,要把新光线再逐像素、逐三角形求交
- 因此,寻求加速的方法
普通方法
- 思路
- 三角形一定在平面内
- 首先做三角形跟平面求交,找到交点再判断是否在三角形内
- 定义平面
- 定义平面上任意一个点 $\bold p’$ + 一个法向量 $\bold N$
- $\bold p:(\bold p-\bold p’)\cdot \bold N = 0$,展开得 $ax+by+cz+d=0$
- 变成了光线跟隐式平面求交问题

- 求光线跟平面的交点
- 联立,求解 $(\bold p-\bold p’)\cdot\bold N=(\bold o+t\bold d-\bold p’)\cdot \bold N=0$
- 得 $t=\frac{(\bold p’-\bold o)\cdot \bold N}{\bold d\cdot\bold N}$
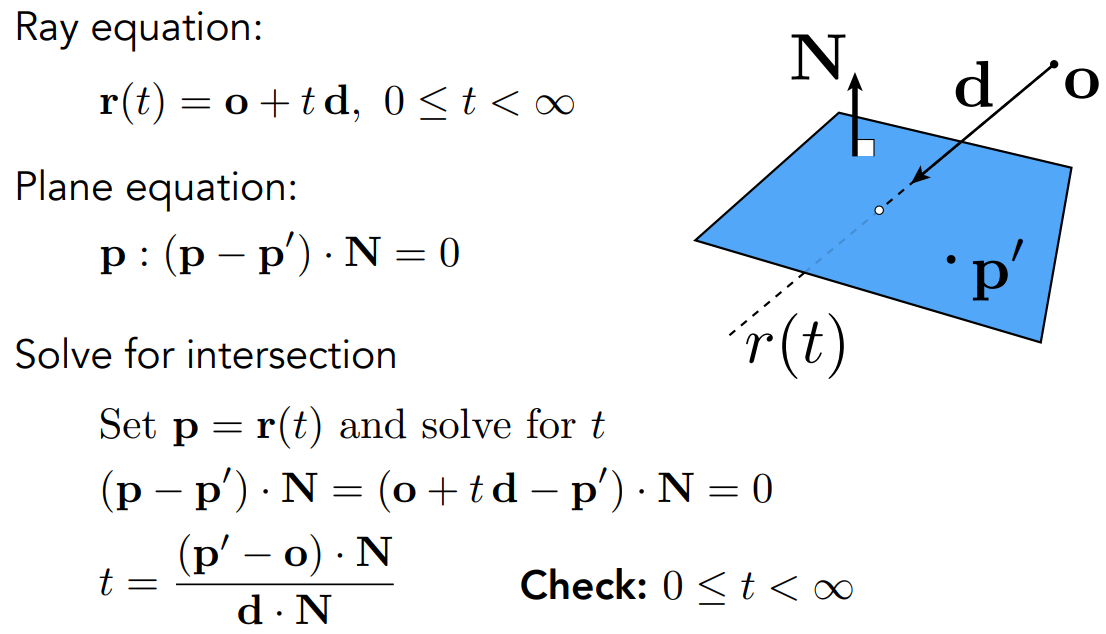
- 检查点是否在三角形内部,用到之前讲的向量叉乘、查看是否同方向
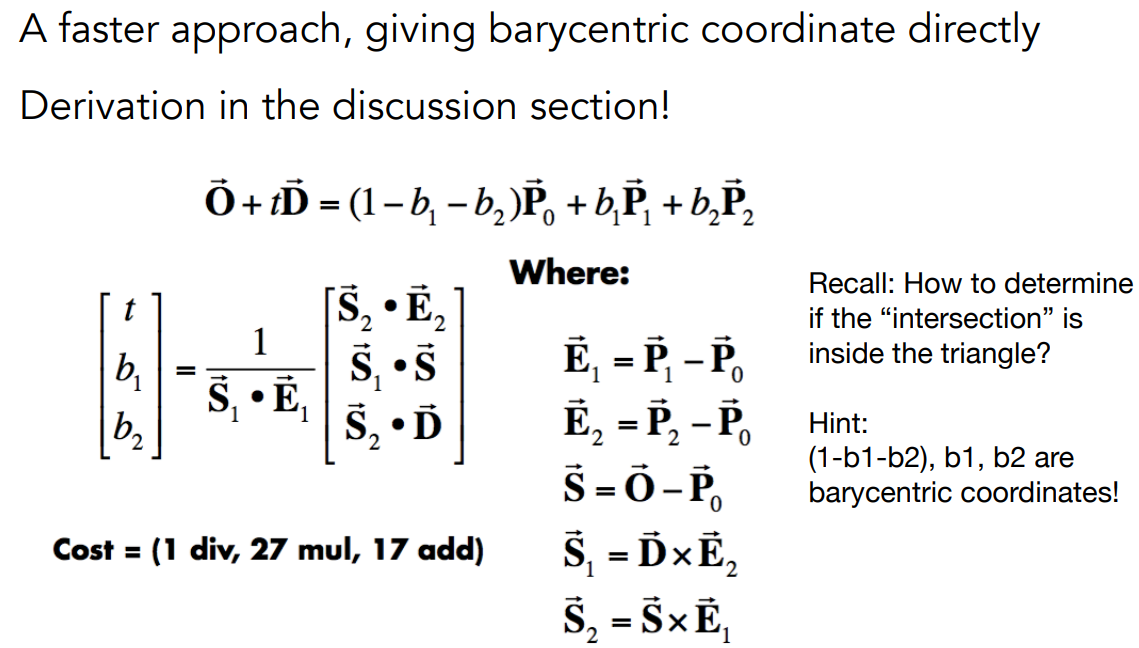
Moller Trumbore Algorithm
- 不用分两步先求光线跟平面交点、再判断交点在三角形内,可以直接求光线跟三角形的交点
- 用重心坐标描述三角形平面上交点的位置 $(1-b_1-b_2)\bold{\vec P_0} + b_1 \bold{\vec P_1} + b_2\bold{\vec P_2}$
- 联立,求解 $\bold {\vec O} +t \bold {\vec D} = (1-b_1-b_2)\bold{\vec P_0} + b_1 \bold{\vec P_1} + b_2\bold{\vec P_2}$
- 三个未知数 $t,b_1,b_2$;三个维度的三个方程
- 如果得出 $1-b_1-b_2,b_1,b_2$ 都是非负,可以立刻判定点在三角形内
- 具体计算方法如图
4 - Axis-Aligned Bounding Boxes(AABBs)
光线跟显式表面求交之二——Bounding Volumes
之前说过,逐像素、逐三角形求交计算量太大,无法接受,因此采用加速方法。前面讲了普通方法(分两步)和 Moller Trumbore 算法(直接求)。
还有别的加速方法:
- Bounding Volumes:用简单的形状把物体包起来
- 如果光线碰不到包围盒,那么一定碰不到里面的物体表面

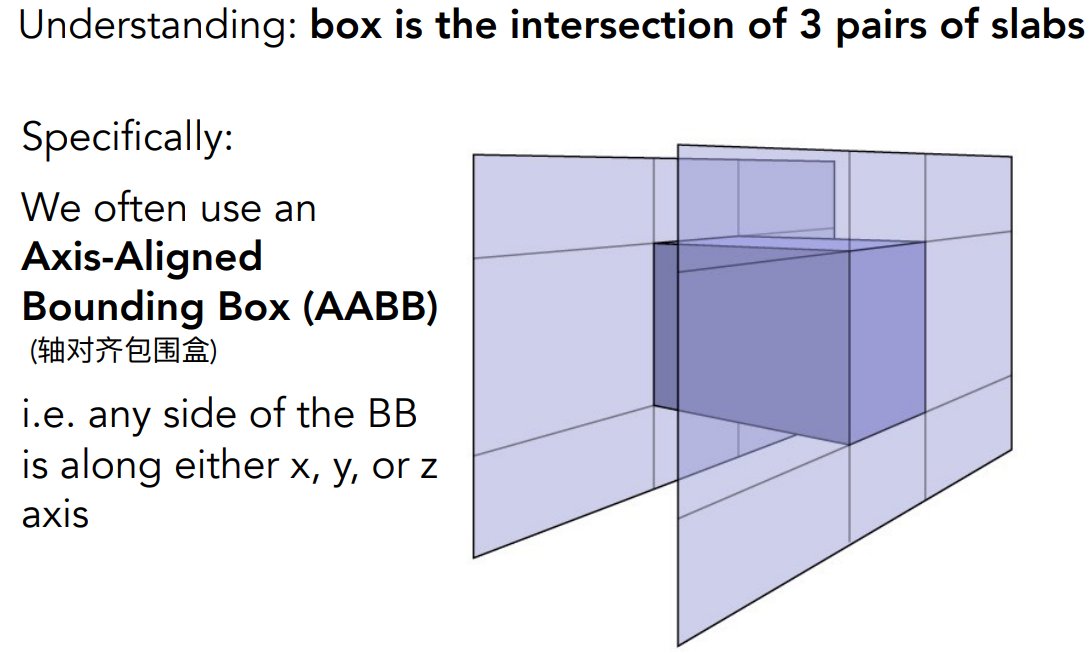
- 把长方体理解为:三个“对面”形成的交集
- 通常,使用 Axis-Aligned Bounding Box(轴对齐包围盒,AABB),长方体的面沿着坐标轴
- AABB的好处:计算方便
- 如图,对于任意平面,光线跟平面求交点的计算稍复杂,需要跟法向量 $\bold N$ 做点乘
- 如果平面跟坐标轴平行,可以直接用距离在轴上的分量、除以方向(法向量也就是速度)在轴上的分量,就得到时间 $t$ 。如图,就是把 $x$ 方向的距离跟时间相除
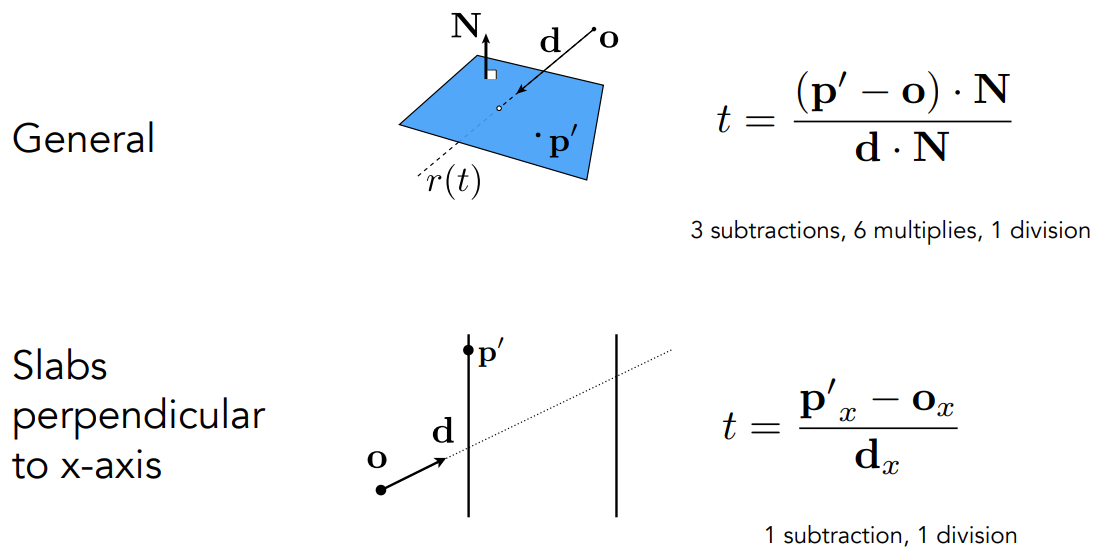
光线跟AABB求交
以2D来考虑,包围盒是两个“对面”形成的交集
对于每个“对面”,求出光线进、出的时间(先假设光线是直线,$t$ 可以< 0)
- “对面”的两个平面分别计算 $t$
- 对于两个竖直平面,在 $t_{min}$ 光线跟左边平面相交,在 $t_{max}$ 光线跟右边平面相交
- 对于两个水平平面,在 $t_{min}$ 光线跟底部平面相交,在 $t_{max}$ 光线跟顶部平面相交
- “对面”的两个平面分别计算 $t$
求线段的交集,就得到光线进、出包围盒的时间
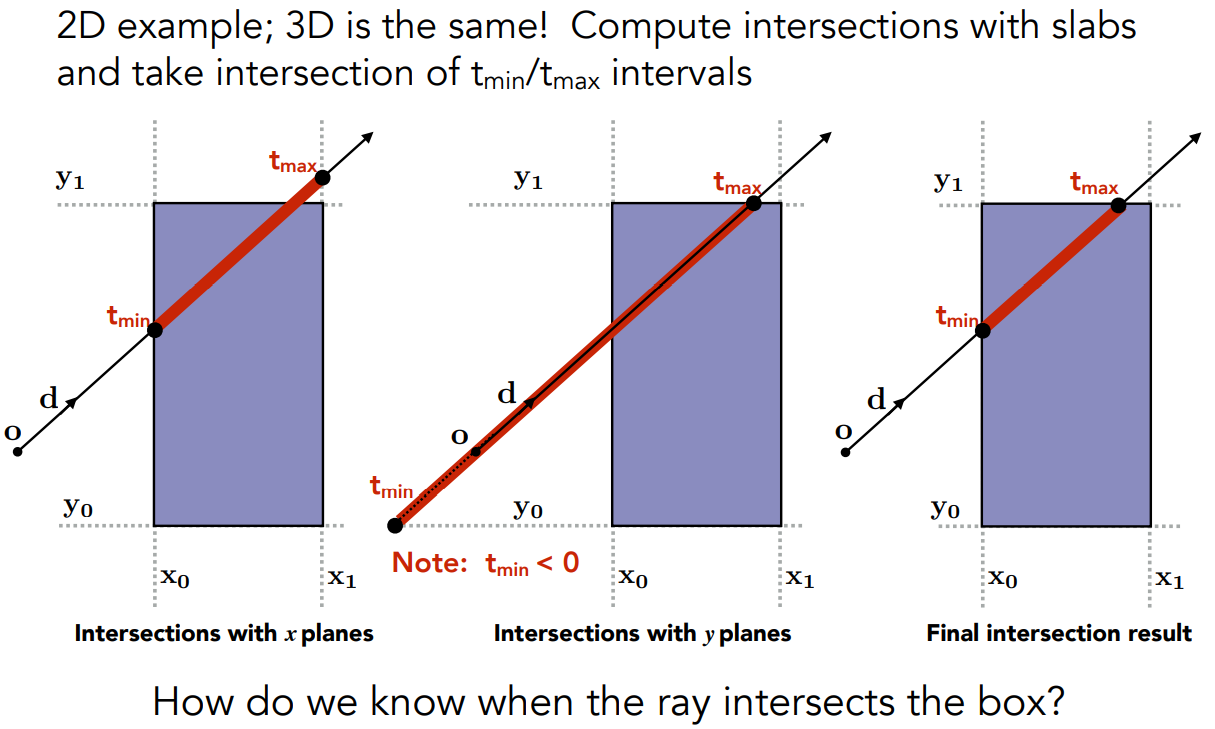
为什么求线段的交集?从3D考虑
- 只有当光线进入所有的“对面”,光线才进入了包围盒
- 只要光线离开任意一个“对面”,光线就离开了包围盒
3D场景的做法
- 对3个“对面”,计算 $t_{min},t_{max}$
- 取 $t_{enter}=\max(t_{min}),t_{exit}=\min(t_{max})$
- 如果 $t_{enter}<t_{exit}$,说明光线跟包围盒有交点(光线在这一段时间进入了包围盒)
光线是射线而不是直线
- 如果 $t_{exit}<0$,说明包围盒在光线的背后,不可能有交点
- 如果 $t_{enter}<0$、 $t_{exit}≥0$,说明光源在包围盒内部,光线一定跟包围盒有交点
综上,当且仅当 $t_{enter}<t_{exit}$ && $t_{exit}≥0$,光线跟AABB有交点


Lecture 14 - Ray Tracing 2 (Acceleration, Radiometry)
在讲这节课的时候,GTC2020有一些新技术
- DLSS 2.0,使用深度学习的超分辨率算法
- RTXGI,实时渲染中的全局光照。之后会讲离线渲染的全局光照
- 随着RTX的发展,很多离线的算法都能搬到实时中来
- 就算实时光线追踪普及,老的实时渲染算法(光栅化)也依然有一定的价值
上节课说到了AABB,以及光线如何跟AABB求交。如何应用AABB,来加速光线跟物体求交?
- 使用AABB来加速光线追踪
- Uniform grids 均匀格子
- Spatial partitions 空间划分
- 注意,这都是在光线已经跟AABB相交的前提下,在AABB内、求光线跟物体相交的加速方法
- Basic radiometry 辐射度量学
1 - Uniform Spatial Partitions (Grids) 均匀格子
思路
- 认为:计算光线跟盒子求交是简单的,计算光线跟物体求交是困难的
- 整体思路:场景中有若干包围盒,先判断光线是否跟包围盒相交;如果相交,再判断光线是否跟包围盒内的物体相交
- 在第二步的包围盒内使用均匀格子,加速判断光线跟物体相交
步骤
- 场景预处理
- 把包围盒划分成格子
- 标记跟物体表面相交的格子
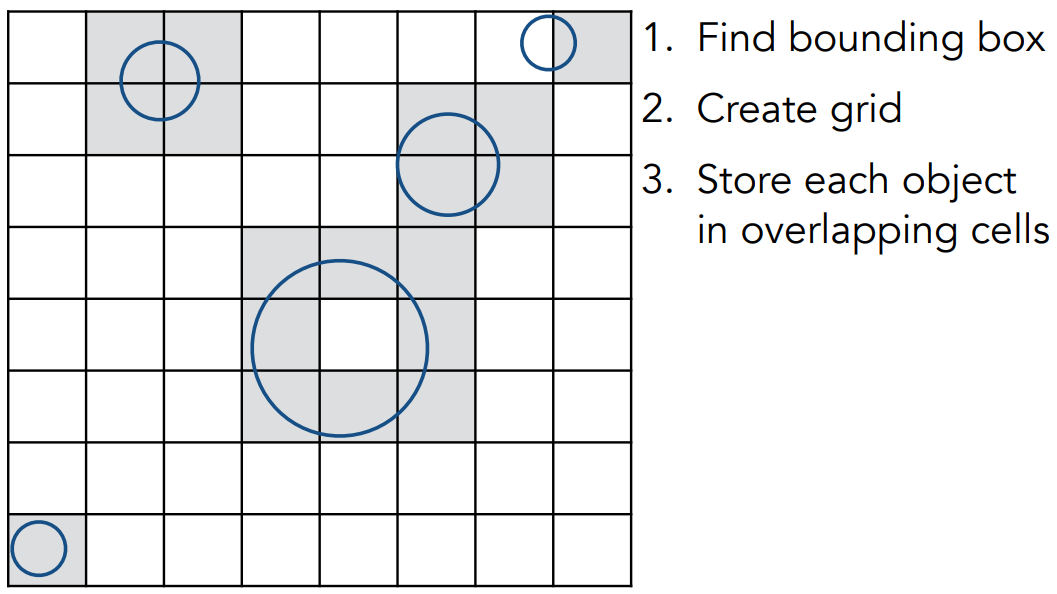
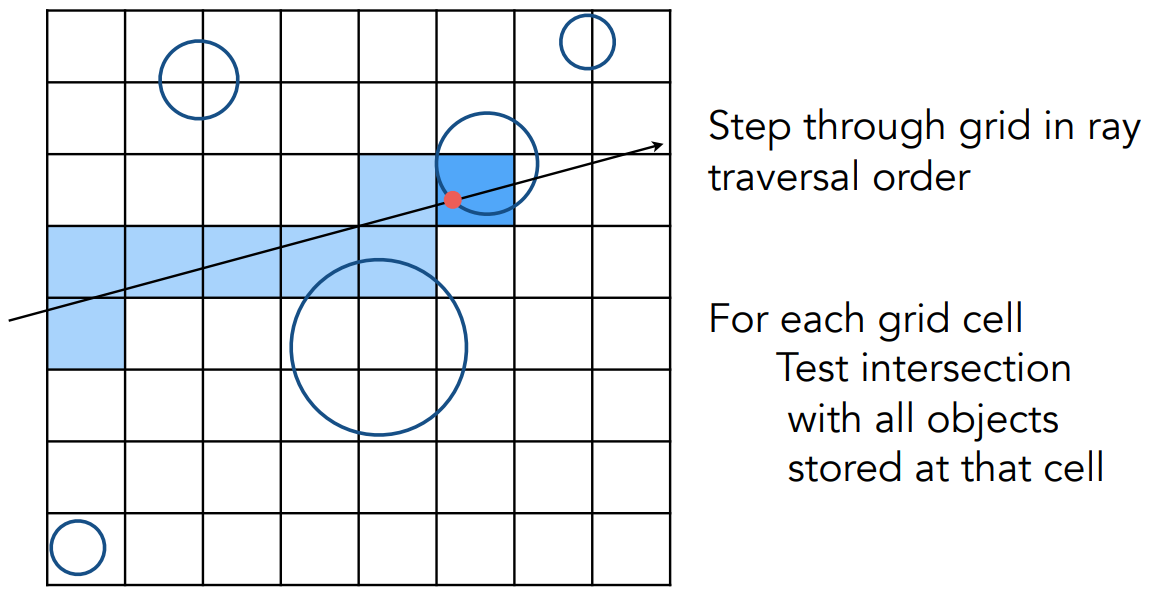
- 首先计算光线跟格子相交;如果格子内有物体,就做一次光线与物体求交
- 对于计算光线跟格子相交,不需要计算所有的格子。使用把光线的光栅化思想(bresenham,HW1里有),可以得到光线往那个方向去、下个格子是谁
- 对于计算光线跟物体相交,可以按照之前讲的跟三角形求交的方法做
加速效果分析
trade-off:格子不能太稀疏也不能太密集
格子越稀疏,如整个空间只有一个格子,没有加速的意义
格子越密集,做光线与格子求交更频繁
通过启发式的算法,计算出比较合理的格子划分方法是:#cells = C * #objs,3D空间C≈27
- 也就是划分27倍物体个数的格子
不同的场景,想要划分的格子也不一样
- 出现大规模集中或大规模空白的场景,不适合均匀划分格子
2 - Spatial Partitions 空间划分
树形空间划分方法
物体分布稀疏的地方可以少划分格子,物体密集的地方多划分格子。
当划分到足够少的物体,就停下来、不再划分。并且组织成树结构:
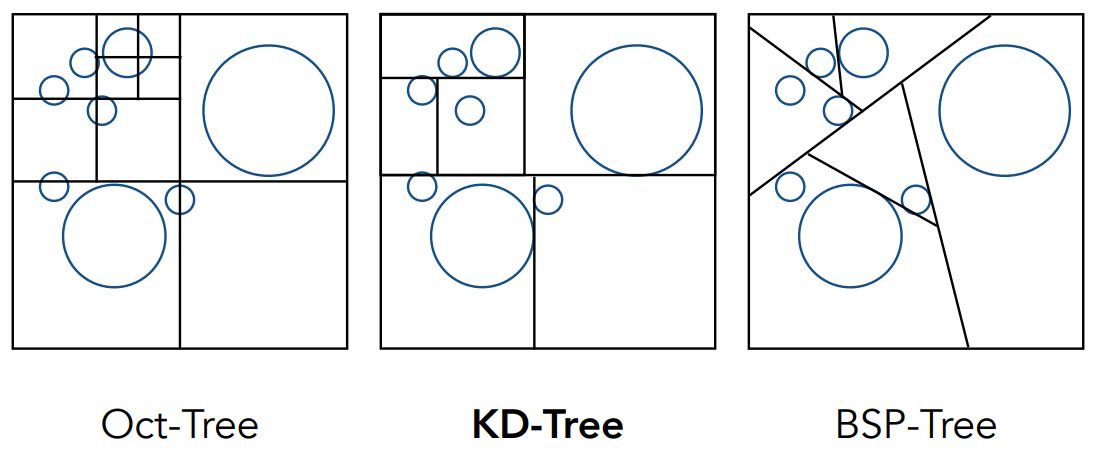
Oct-Tree 八叉树
- 把3D空间均匀划分成8份
- 缺点是如果维度继续上升,树的叉会指数级增长
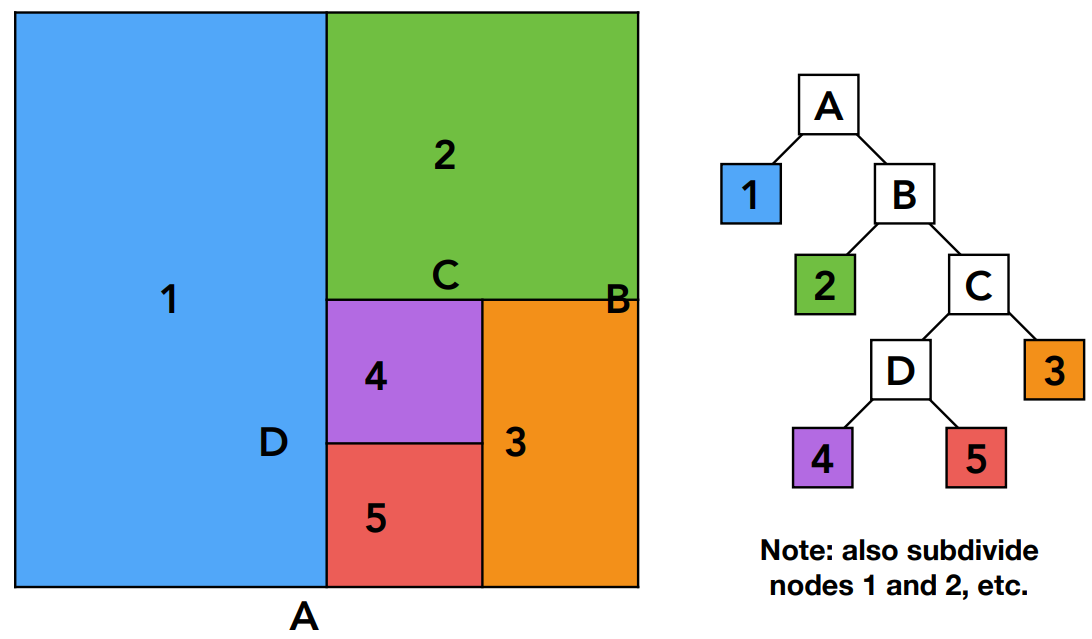
KD-Tree
- 空间能得到划分,并且跟维度无关
- 首先水平划分,形成两个格子;每个再竖直划分,分别形成两个格子;继续下去
- 如果是3D,就是沿x、沿y、沿z循环划分
- 可以保证空间的均匀划分,并且保持了二叉树的性质
BSP-Tree
- 空间的二分划分
- 每次选一个方向把空间分开,不同的空间再分开,只是不是横平竖直地分开
- 由AABB类比,斜着的线计算上不如 KD-Tree(AABB的优越性就是AA简化了光线跟平面交点的计算);在高维情况下,也会越来越不好计算(3D要用平面划分,再高维用超平面)
KD-Tree
上图是以一边为例的KD-Tree,实际上每个区域都会继续划分,总体是一个二叉树
- 在中间结点,只需记录被划分成什么样的格子
- 在叶子节点实际存储跟格子相交的几何形体
设计具体的数据结构,来存储KD-Tree
- 对于任何结点,需要知道
- 沿着哪个轴进行划分
- 划分的位置(不一定是中间)
- 两个子节点的指针
- 叶子节点存储实际的几何物体
在进行光线追踪之前,会把这个加速结构建立好。这个结构如何帮助我们做光线追踪的加速?
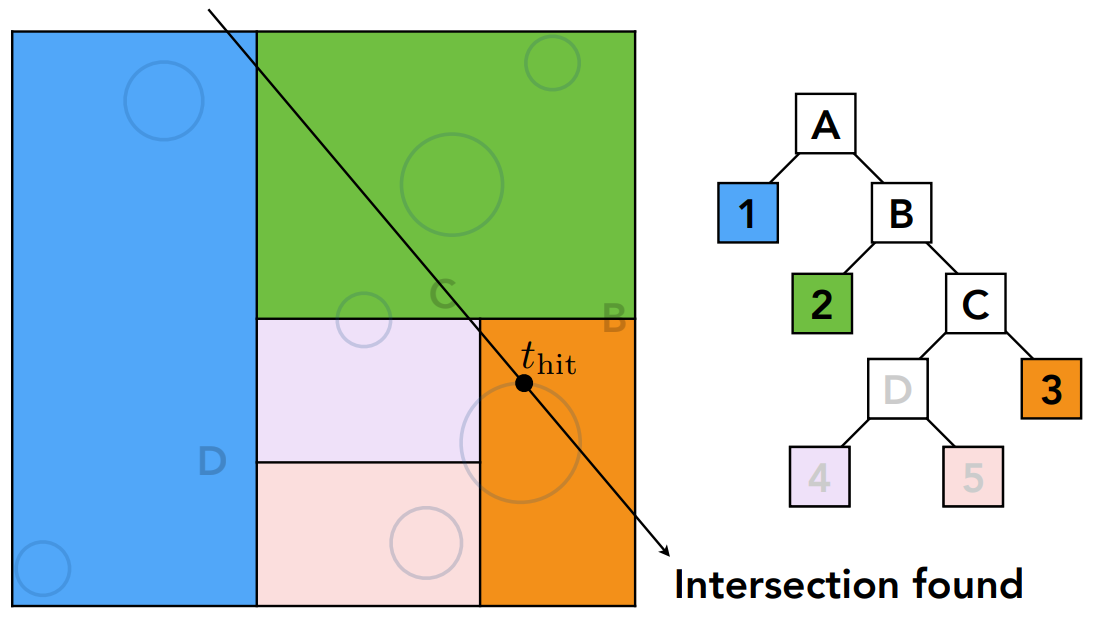
- 光线经过某个结点,就判断光线跟某个结点是否有交点
- 如果没有,什么都不做(跟包围盒不相交,就不可能跟其中物体相交)
- 如果有,则可能跟两个子结点有交点
- 判断是否跟两个子结点相交,如果相交则继续判定
- 如果是叶子结点,就跟结点内所有物体求交
- 以下图所示的结构为例,首先跟A相交,就判断跟1、B是否相交,然后判断2、C,3、D,到了3是叶子结点,就计算光线跟3中所有的物体求交
其他问题
- 知道了划分格子的方法,以及搜索的方式,还有一个问题:如何判定格子跟物体有交集?也就是如何判定物体存到哪个叶子结点
- 这是一个难点,需要判定一个3D立方体是否跟一个三角形有交集
- 有各种相交的情况,不能单纯通过顶点判断
- 这是一个难点,需要判定一个3D立方体是否跟一个三角形有交集
- 一个物体,可能跟很不同的格子有交点,那么在多个叶子结点中都要存这个物体
- 一个物体可能出现在多个叶子结点中,这个性质不好
- 概括来说,KD-Tree①物体可能存在于不同的格子里②建立并不简单,需要考虑三角形与格子的求交。由于这些问题的存在,KD-Tree在近10年用得少了
因此,寻求其他的划分方法,不从空间做起、而从物体做起
3 - Object Partitions & Bounding Volume Hierarchy (BVH)
在目前的图形学,不管做实时光线追踪还是各种离线的结构,BVH是被普遍应用的,它解决了KD-Tree的两个问题。
BVH结构
BVH的划分步骤
把一个盒子里的所有三角形组织成两部分,存在一些划分技巧
沿哪个轴划分
- 可以用KD-Tree相似的划分方法,即各个轴循环,得到尽量均匀的划分结果
- 也可以用不同技巧,比如每次按照最长的轴划分成两部分
在哪个位置划分
- 取“中间”的物体,如果有 n 个三角形,取中位数第 n/2 个三角形
- 所有三角形重心沿某个轴排序,O(nlogn)
- 任意一列数找第 i 大的数,都可以在 O(n) 时间解决:快速选择算法(TopK)
- 保证两部分的物体数量差不多,也就是保证树接近平衡
- 取“中间”的物体,如果有 n 个三角形,取中位数第 n/2 个三角形
我的理解:某种意义上,这样划分让BVH更加接近平衡二叉树,查找更快
对于这两个部分,分别再求它们的包围盒
再递归划分包围盒
当叶子结点内有足够少的三角形就可以停下了,同样将实际物体记录在叶子结点中
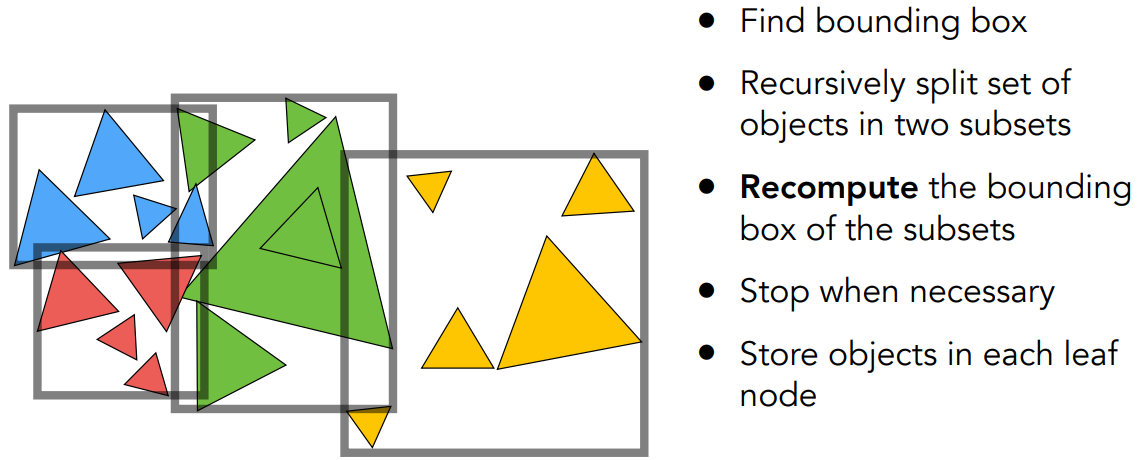
以上图为例
- 首先在水平方向,把所有三角形分成红蓝、黄绿两部分,然后划分包围盒
- 对于红蓝,纵向坐标更长,因此纵向划分成红、蓝两部分,求各自的包围盒
- 同样,对于黄绿,横向坐标更长,取个数中间的三角形,划分成两部分,再分别求新的包围盒
BVH的性质
避免了KD-Tree的老问题
一个物体只可能出现在一个格子中
给一堆三角形求包围盒是容易的,取所有维度上顶点坐标的最小最大值即可
省去了三角形跟格子求交的事情
带来一个新问题
- 对空间的划分不严格,不同的包围盒可以相交
- 对于每个三角形划分到哪个区域,图中是比较好的划分。也有不同包围盒相交特别多的情况
- 因此,关于怎样更好地划分,有很多不同的研究
当物体位置移动,或者加了新物体,就需要重新计算新的BVH
BVH的数据结构
- 中间结点
- 包围盒
- 两个孩子指针
- 叶子结点
- 包围盒
- 实际的物体
BVH伪代码
Intersect(Ray ray, BVH node){
// 不相交
if(ray missed node.bbox) return ;
// 相交,是叶子结点,就查找所有物体
if(node is a leaf node){
test intersection with all objs;
return closest intersection;
}
// 相交,不是叶子结点,就查找子结点
hit1 = Intersect(ray, node.child1);
hit2 = Intersect(ray, node.child2);
return the closer of hit1, hit2;
}物体划分和空间划分
我的理解:对于AABB内部的空间,前面讲了各种划分方法。实际上,一种是按照空间划分,在划分过程中忽略物体跟空间的关系,也带来了两个问题,分别是物体归属多个格子、树难建立;而BVH是按照物体进行划分,再建立各自的包围盒作为格子空间
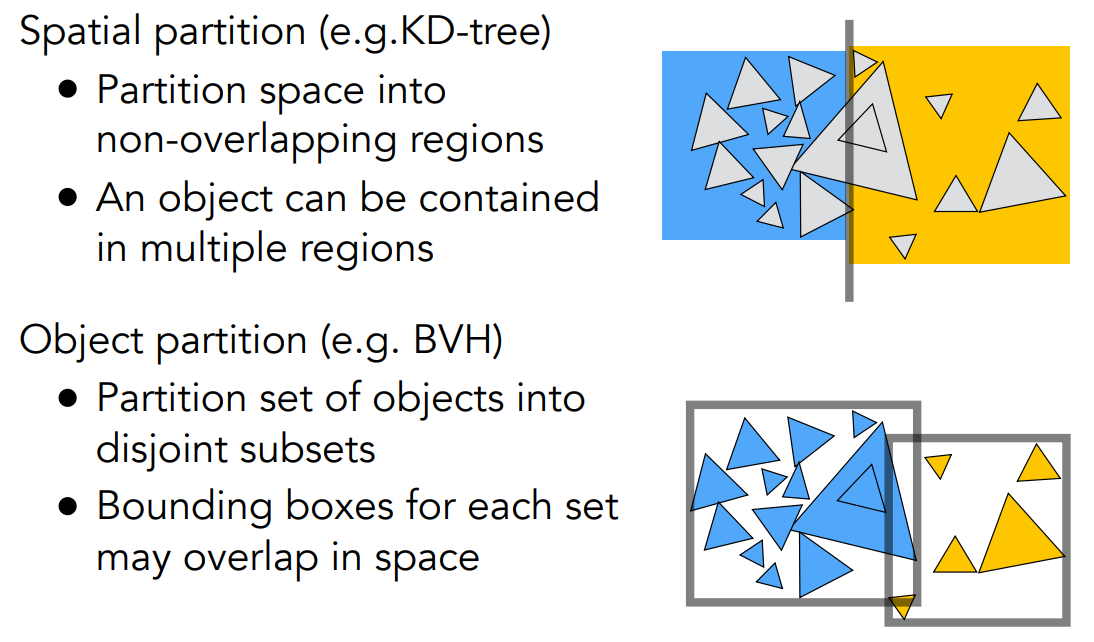
- 按照空间划分(KD-Tree)
- 物体可能存在于多个格子
- 需要计算三角形跟包围盒相交问题
- 按照物体划分(BVH)
- 物体只存在于一个格子
- 不同的包围盒可能有相交
到此,光线跟场景的求交都讲完了(光线跟三角形、AABB、各种加速结构求交)。这些都是 Whitted-Style 光线追踪的内容。
以下就是非Whitted-Style的内容。
4 - Basic Radiometry 辐射度量学
为了更好地模拟真实世界中的光照,需要引入辐射度量学的基础内容。
动机
前面成像方法的问题
HW3,实现了Blinn-Phong光照模型,其中光的强度 $I$ 的物理意义是什么?
- $\begin{array}{ll}L = L_a + L_d + L_s = k_aI_a+k_d (I/r^2)\max(0, \bold {n\cdot l})+k_s(I/r^2)\text{max}(0, \bold n\cdot\bold h)^p\end{array}$
- 光栅化的shading过程,有些数值只用作计算,没有实际的物理意义
Whitted-Style光线追踪,得到的图像看上去真实吗?
- 在很多地方的计算做了简化,比如反射、折射的能量衰减方式
辐射度量学:在物理上准确定义光照的方法
- 把光精确地定义出来,包括物体表面跟光如何精确地作用
- 定义3D空间中光的一些属性(无时间)
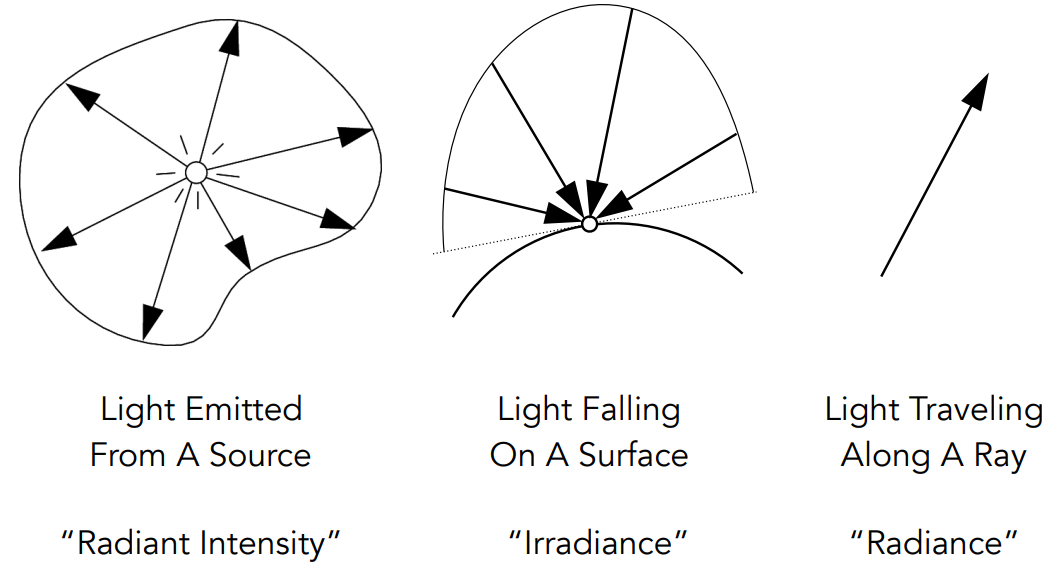
- radiant flux,intensity,irradiance,radiance
- 翻译过来可能是:辐射通量,辐射强度,辐射照度,辐射亮度
- 依然基于几何光学来做(光是直线而不是波)
属性一:Radiant Energy and Flux (Power)
Energy:能量 [J];Flux (Power):功率 [lm]
物理量定义
- Radient Energy:电磁辐射的能量,用焦耳表示
- Radient energy is the energy of electromagnetic radiation. It is measured in units of joules, and denoted by the symbol:
- $Q\space [\text{J=Joule}]$
- Radient flux / power:单位时间的能量(功率)
- Radiant flux (power) is the energy emitted, reflected, transmitted or received, per unit time.
- $\Phi \equiv\frac{\text{d}Q}{\text{d}t} \space[\text{W=Watt}] \space[\text{lm=lumen}]^\bold *$
- 为了分析能量变化,自然需要定义单位时间的能量。在整套辐射度量体系中,考虑的都是单位时间的性质
- 类比power,如灯泡的功率(亮度)是多少瓦特。在辐射度量学中使用lumen作为flux的单位
- 另外一个角度定义flux:给定单位时间,通过平面的光子数量就是flux
- 用 flux 衡量一个点光源的总亮度
- 通过energy和power,定义其他的物理量,如:光源辐射的能量(Radiant Intensity),物体表面接收多少能量(Irradiance),光在传播中的能量(Radiance)
属性二:Radiant Intensity
Intensity:单位立体角上的能量;立体角:空间中的一个角度
角和立体角
The radiant (luminous) intensity is the power per unit solid angle emitted by a point light source.
- power per unit solid angle:单位立体角上的flux
- $I(\omega)\equiv\frac{\mathrm d \Phi}{\mathrm d\omega}$
- 单位:$[\frac{\text W}{\text {sr}}]\space[ \frac{\text{lm}}{\text{sr}}\text{=cd=candela} ]$
角和立体角
- 角(弧度)
- 用弧度来定义一个角 $\theta = \frac{l}{r}$,弧长和半径同步放大不影响角度的大小
- 圆对应的 radians 是 $2\pi$
- 立体角是角在3D空间中的延申
- 从球心出发,形成一个锥,打到球面上形成一个面积
- $\Omega=\frac{A}{r^2}$
- 整个球对应的 steradians 是 $4\pi$

- 角(弧度)
微分立体角
- 通过 $\theta,\phi$ 可以定义球面上唯一的方向,分别表示向上方向的夹角、绕向上方向的偏转角度
知道了一个方向 $\omega$,就可以求出这个方向上的单位(微分)立体角 $\mathrm d\omega$
在球上一个单位的面积为 $\mathrm dA=(r\mathrm d\theta)(r\sin \theta \mathrm d\phi)=r^2\sin\theta\mathrm d\theta\mathrm d\phi$ ,矩形面积
微分立体角是单位面积除以 $r^2$,即 $\mathrm d\omega=\frac{\mathrm dA}{r^2}=\sin\theta\mathrm d\theta\mathrm d\phi$
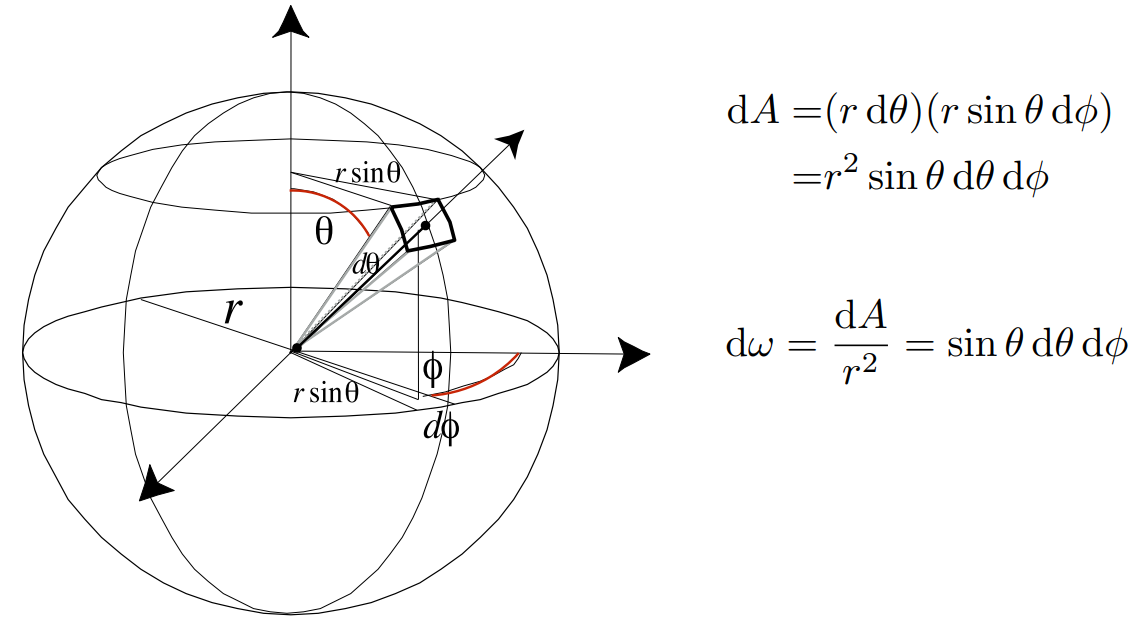
把整个球上的单位立体角积分,肯定就是 $4\pi$
- $\Omega=\int_{S^2}\mathrm d\omega=\int^{2\pi}_{0}\int^{\pi}_{0}\sin\theta \mathrm d\theta \mathrm d\phi=4\pi$
总结:在辐射度量中,如果表示三维空间的一个方向,通常使用 $\omega$ 来表示。可以通过 $\theta,\phi$ 定义它的位置,并且可以通过 $\sin\theta \mathrm d\theta\mathrm d\phi$ 算出它的微分(单位)立体角。
微分立体角的含义是:当 $\theta,\phi$ 各变化一点点,会引起多大的立体角的变化
回到 Intensity 上来
- 定义一个点光源的 flux,作为它的总亮度
- intensity 是光源在任何一个方向上的亮度
- $\Phi=\int_{S^2}I\mathrm d\omega=4\pi I$,可以通过积分计算总的 flux
- $I=\frac{\Phi}{4\pi}$ ,可以计算任何方向上光的 intensity
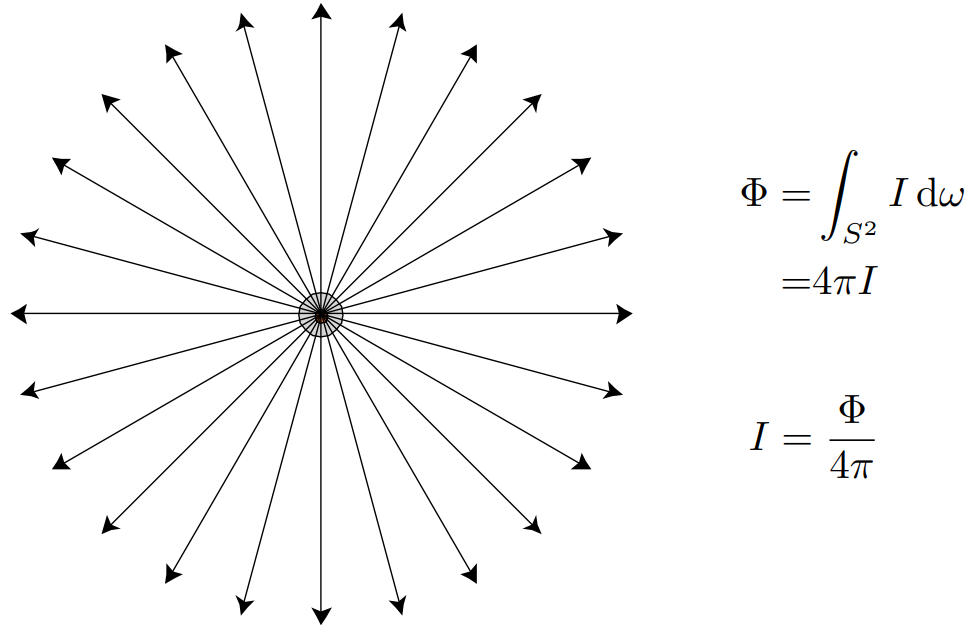
- 以一个灯泡举例
两个属性总览:
属性三:Irradiance
Irradiance:单位面积上的能量
irradiance
- The irradiance is the power per (perpendicular / projected) unit area incident on a surface point.
- power per unit area:$E(\bold x)\equiv\frac{\mathrm d\Phi(\bold x)}{\mathrm dA}$ ,入射单位面积上的能量(flux)
- 单位:$[\rm \frac{W}{m^2}]\space[\frac{lm}{m^2}=lux]$
- 默认都是垂直入射。跟Blinn-Phong光照模型的漫反射的 Lambert’s Cosine Law 一样,如果光照不是直射,需要乘以 $\cos\theta$
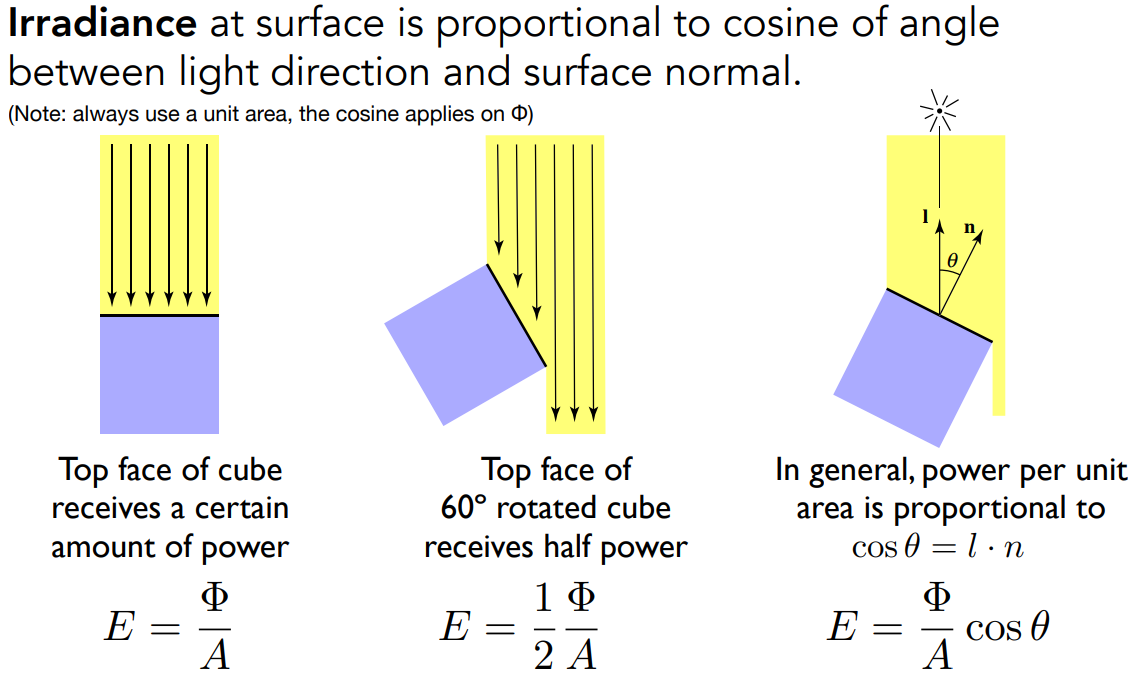
- 用 irradiance 分析光照传播的递减:
- 本质上,立体角没变,intensity 也没变,irradiance 以 $r^2$ 在衰减
- 在辐射度量学里,Intensity 是不变的,因为是固定的立体角,随着传播,面积会变大。真正缩减的是 irradiance。在之前,Blinn-Phong 模型认为衰减的是 Intensity
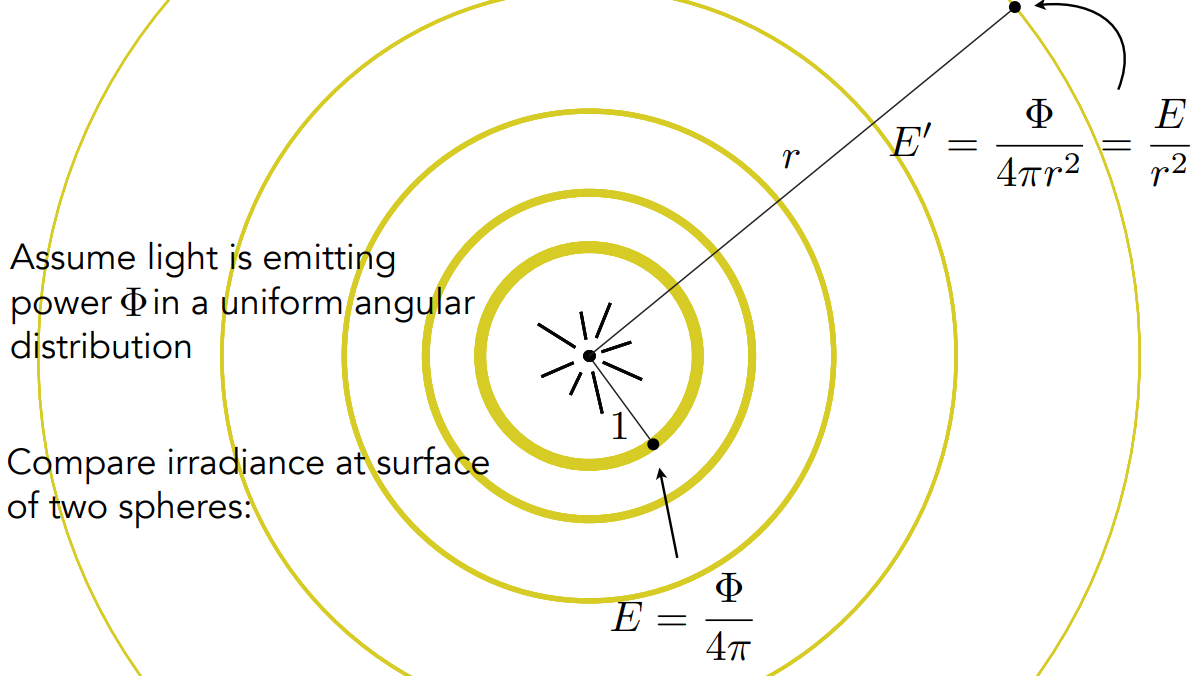
属性四:radiance
动机
- Radiance is the fundamental field quantity that describes the distribution of light in an environment
- Radiance is the quantity associated with a ray,定义 radiance 是为了用来描述光线的一些属性
- Rendering is all about computing radiance,光线追踪需要计算
定义
- The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area.
- 在单位立体角、并且在单位投影面积上的能量
- 有一个单位大小的面,从这个面、向某一个方向上辐射出的能量。微分两次的概念
- 面的大小可能不同,考虑单位大小
- 面会向各个方向辐射能量,考虑某一个方向
- $L(\mathrm p, \omega)\equiv \frac{\mathrm d^2\Phi(\mathrm p,\omega)}{\mathrm d\omega\mathrm dA\cos\theta}$
- 单位:$[\rm \frac{W}{sr\space m^2}]\space [\rm\frac{cd}{m^2}=\frac{lm}{sr \space m^2}=nit]$
- 把 radiance 跟 irradiance、intensity 联系起来
- 定义
- radiance:power per unit solid angle per projected unit area
- irradiance:power per projected unit area,光源发出的能量入射到单位面积
- intensity:power per solid angle,光源在任意方向的flux
- 因此
- radiance:irradiance per solid angle
- radiance:intensity per projected unit area
- 定义
- 以两种方式理解 Radiance
- Incident Radiance,从接收能量理解(ir-词根的意思是向内)
- radiance 是单位立体角的 irradiance
- irradiance 跟 radiance 的区别:是否有方向性
- radiance 表示从某一个方向照射到单位面积上,并且被接收的能量
- irradiance 表示这个单位面积在所有方向上接收的能量,把所有方向 radiance 积分起来
- $L(\mathrm p, \omega)=\frac{\mathrm dE(\mathrm p)}{\mathrm d\omega\cos\theta}$

- Exiting Radiance,从发出能量理解
- intensity:单位立体角上的能量,radiance :单位(垂直)面积上的 intensity
- 一个小面积向各个方向发出能量,intensity 就是 $\mathrm dA$ 往某个方向辐射出去的能量
- radiance 是单位面积上发出的 intensity
- $L(\mathrm p, \omega)=\frac{\mathrm dI(\mathrm p,\omega)}{\mathrm dA\cos\theta}$

- Incident Radiance,从接收能量理解(ir-词根的意思是向内)
理解 irradiance 和 radiance 的关系
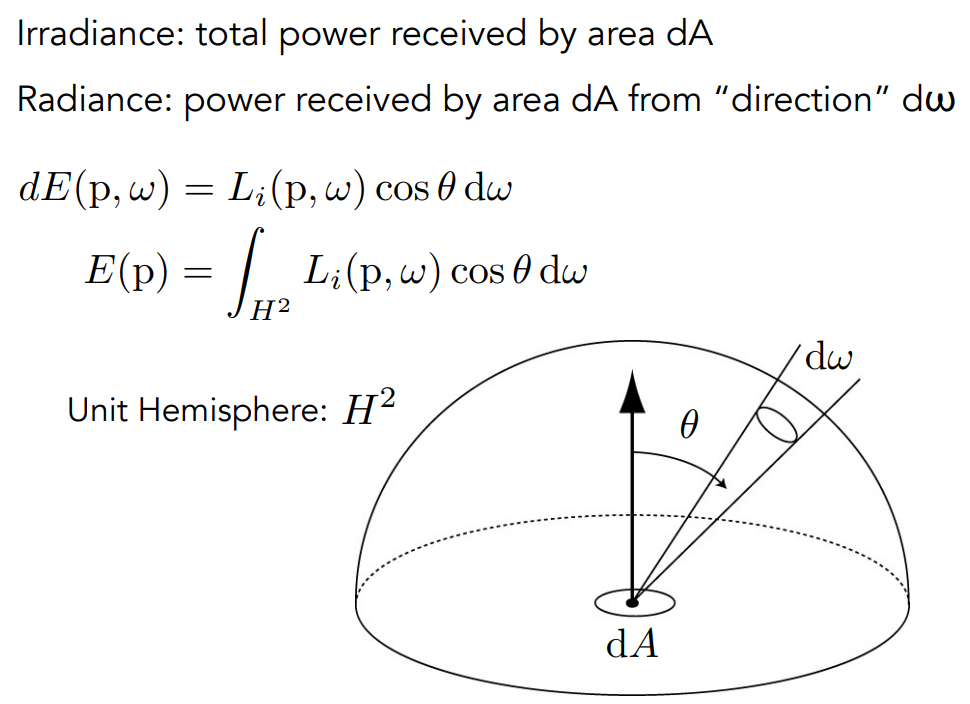
- irradiance:一个小范围收到的所有能量是多少
- radiance:一个小范围收到能量,从某个方向进来收到多少能量
- 图中的微分、积分式把 irradiance 和 radiance 联系起来
有了 Radiance 的概念,就可以定义辐射度量学中的光照了。
Lecture 15 - Ray Tracing 3 (Light Transport & Global Illumination)
通过 irradiance、radiance 的概念,定义所有的物体表面上的光线传播过程
- Light transport
- the reflection equation
- the rendering equation
- Global illumination
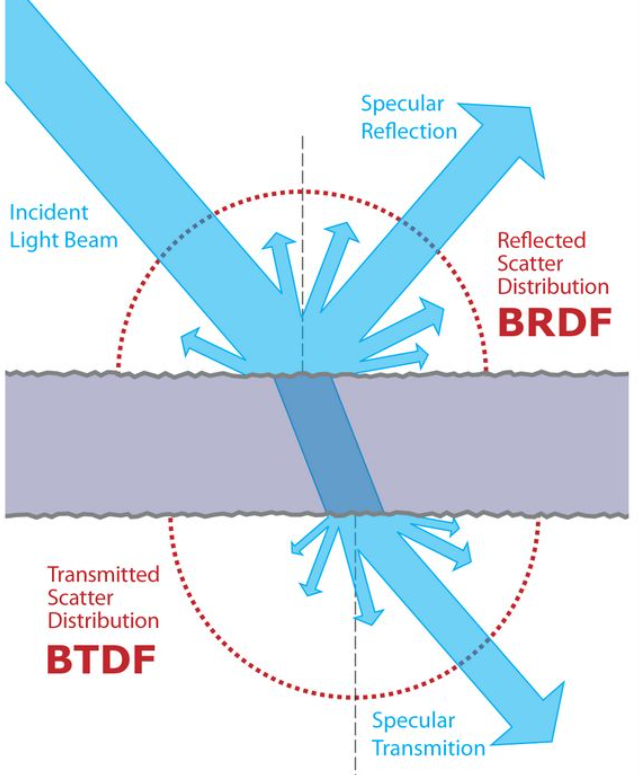
1 - Bidirectional Reflectance Distribution Function (BRDF)
BRDF 双向反射分布函数
由 irradiance、radiance 的概念,已知入射光的能量,射到物体表面会向各个方向辐射。BRDF用于描述:光线从某个方向进来,并反射到某个方向去,它的能量是多少。
- 反射的一种理解:光线打到某个物体表面,被吸收了,物体表面再把这部分能量发出去(经过一个中间过程)
- 一个小区域 $\text dA$,接收到一个方向的光线的能量作为 irradiance,然后反射到各个方向、转化成各个方向的 radiance
- 对于 $\text dA$
- 入射能量:接收到某一个方向立体角的 radiance 的能量,即 $L(\omega_i)\cos \theta_i \text d\omega_i$,这也是这块区域接收的 irradiance $dE(\omega_i)$
- 辐射能量:能量发射到四面八方,每个立体角上的 radiance $dL_r(\omega_r)$

- 即,对于一个单位面积,我们知道它从一个立体角上接收 irradiance,也知道它将会把这些能量发射到各个方向去
- BRDF 定义了:发射能量的方式,能量如何被分配到各个立体角上去。计算各个出射方向的能量的占比,也就是所有出射立体角的 radiance,除以这块区域接收到的总的 irradiance
- $f_r(\omega_i\rightarrow\omega_r)=\frac{\mathrm dL_r(\omega_r)}{\mathrm dE(\omega_i)}$
再次理解 BRDF 的定义:
- 定义 BRDF 函数来描述这个 radiance:考虑微小面积 $dA$,从某一个微小立体角 $d\omega_i$ 接收到的 irradiance,会如何被分配到各个不同的立体角上去
- 对于任何出射方向,算出 radiance $dL_r(x, \omega_r)$,去除以微小面积接收到的 irradiance $dE(\omega_i)$
- 这就是 BRDF,它告诉我们如何把一个方向上收集到的能量反射到其他方向上去
- $f_r(\omega_i\rightarrow\omega_r)=\frac{\mathrm dL_r(\omega_r)}{\mathrm dE(\omega_i)}=\frac{\mathrm dL_r(\omega_r)}{L_i(\omega_i)\cos\theta_i\mathrm d\omega_i}$
- 单位:$[\frac{1}{\rm sr}]$
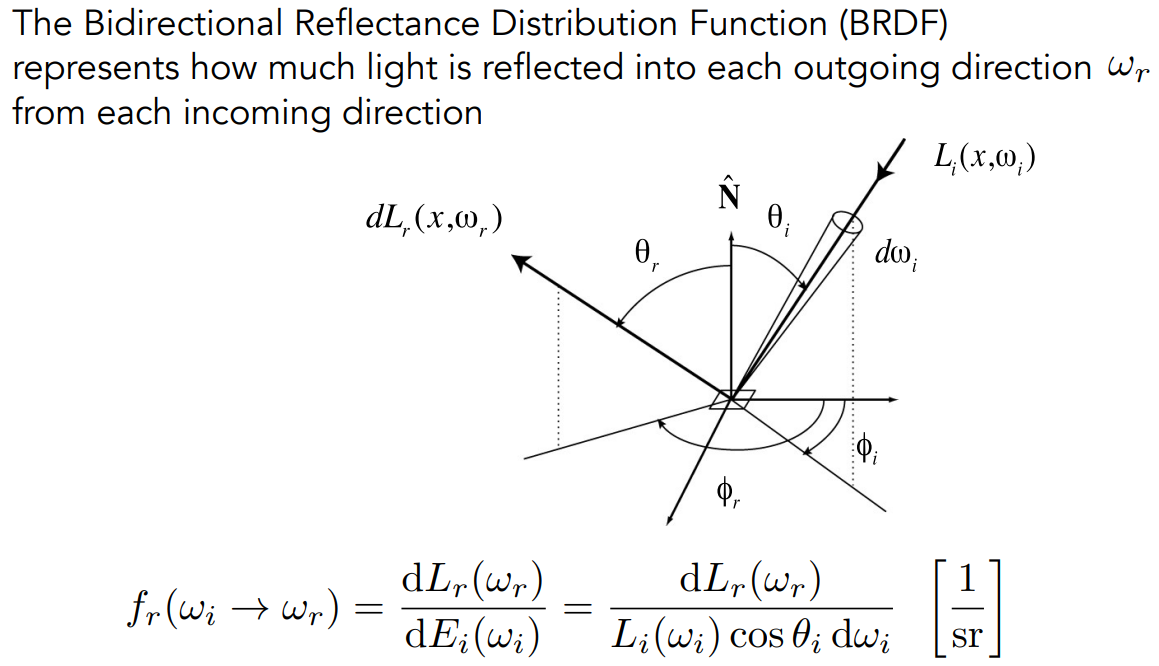
- 以上就是 BRDF 的数学或物理上的定义。如果只从理解的角度来看
总的来说,BRDF 是光照打到物体、进行反射,它的能量分布
- 如果是镜面反射,在镜面反射方向分布了所有能量,非镜面反射方向不会有能量
- 如果是漫反射,接收的能量会被均等地分布到所有方向
概念上,BRDF 描述了光线和物体是如何作用的。BRDF 定义了物体不同的材质是怎么回事
2 - Reflection Equation 反射方程
一个点可以接收四面八方的光照,而 BRDF 定义了每一个方向上接收光照、进行的能量反射情况。
对于每个入射方向,都对应一个BRDF。考虑每一个入射方向,对于出射方向的贡献
- 一个入射方向对于一个出射方向的能量贡献:irradiance = $L_i(\mathrm p,\omega_i)\cos\theta_i \text d\omega_i$
- irradiance 乘以 BRDF(到某个方向的比例),就是反射到出射方向的能量
- 所有半球面方向上的贡献积分起来,就是反射方程,得到在所有入射光下、最后反射到该方向上的能量
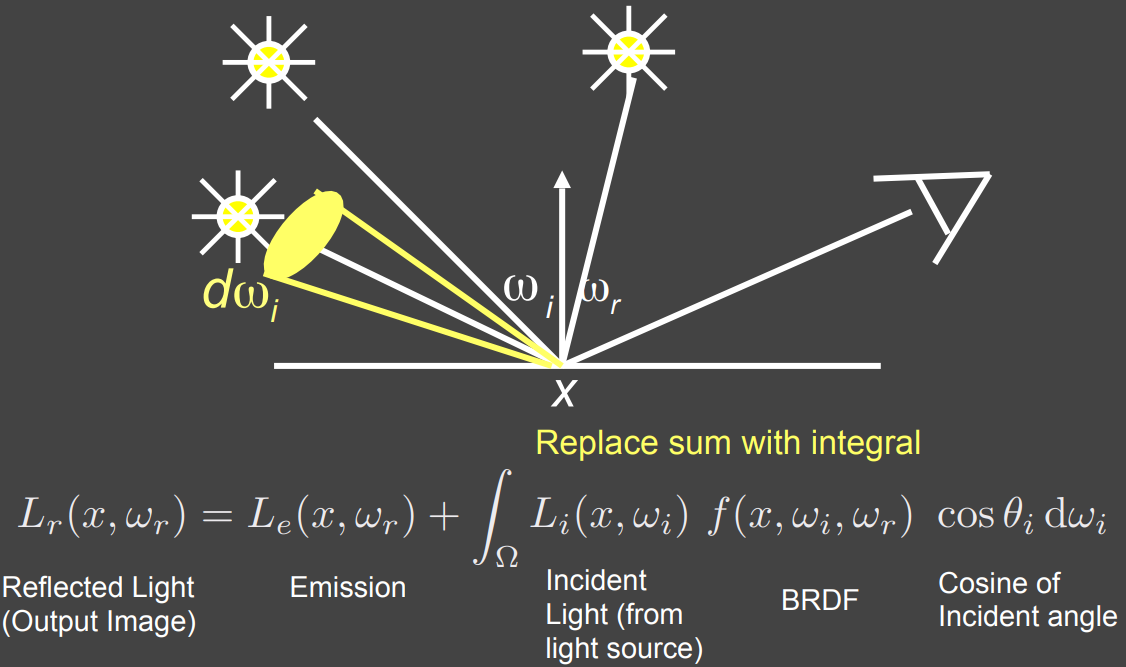
- $L_r(\mathrm p,\omega_r) =\int _{H^2}f_r(\omega_i\rightarrow\omega_r)L_i(\mathrm p,\omega_i)\cos\theta_i\mathrm d\omega_i$
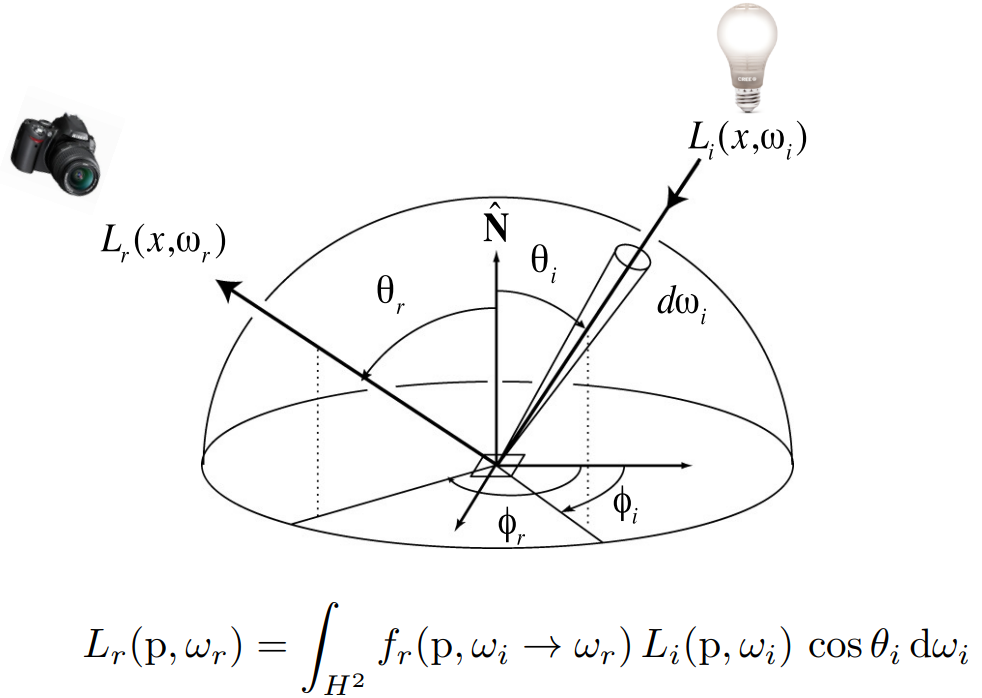
这是一个递归的过程:入射光可能来自光源,也可能是其他物体反射而来的 radiance。之前说的“光线不止弹射一次”也体现在这里。
3 - Rendering Equation 渲染方程
推导
通过反射方程,可以推出更加通用的渲染方程。
反射方程定义了物体反射光线的方法,但没有考虑物体自身会发光的情况。因此把物体发的光加上就可以了。
我们看到一个物体,它对某一个方向出射的光由两部分组成:它自身发的光 + 反射其他光。
通过渲染方程,就用一个公式描述了所有光线的传播。所有限制在物体表面上的光线传播都满足这个方程。
理解
渲染方程再理解
对于一个点光源,最终射出的光 = 自发光 + 反射
对于多个点光源,在反射项是多个反射光线相加
- 灯开得多就越亮,不难理解
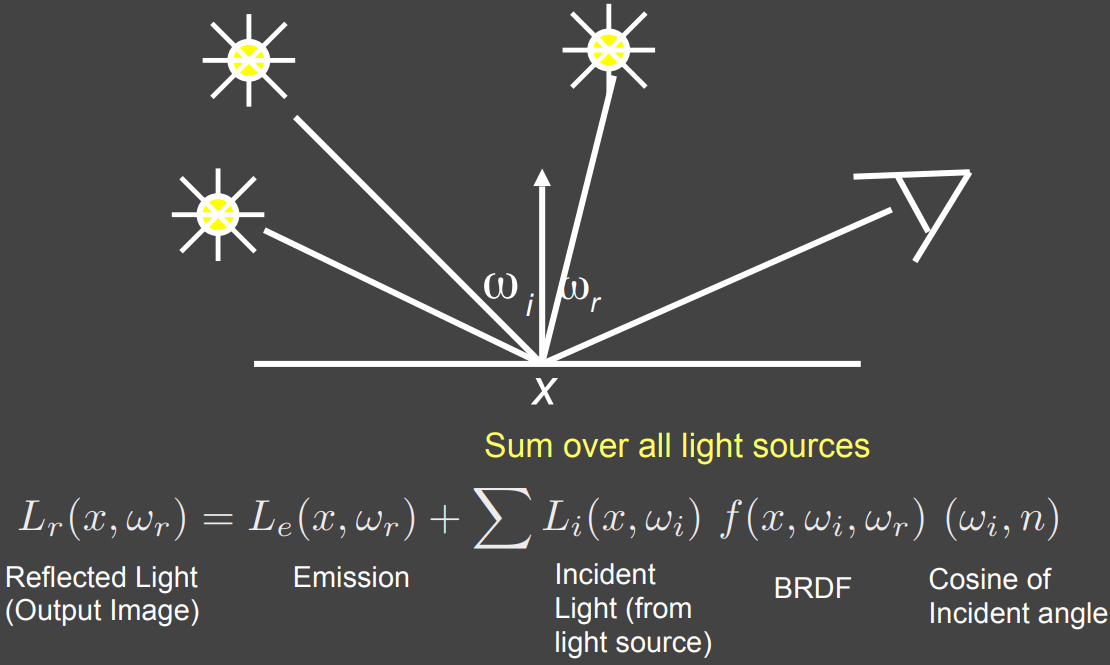
对于面光源,反射项对立体角 $\mathrm d\omega$ 进行积分
如果不是从光源处直接接收光照,而是接收其它反射光
- 这一点 $X$ 往某个方向辐射的 radiance,依赖于其他点 $X’$ 辐射出来的radiance(递归的过程)
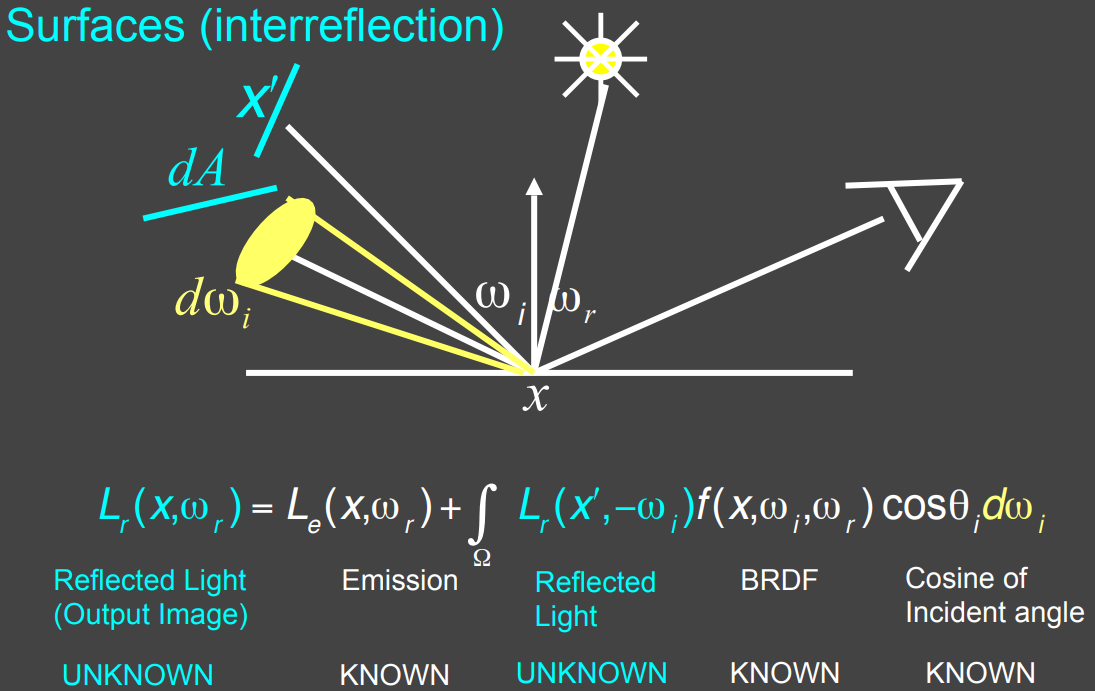
通过递归关系,把方程写成一个简单的形式来理解
- unknown 不知道的项
- 从某个方向看向一个点,不知道看到的能量是多少 $L_r(X,\omega_r)$
- 从其他物体反射到该点的radiance $L_r(X’,-\omega_i)$
- known 知道的项
- 物体的自发光方式 $L_e(X,\omega_r)$
- 物体不同的材质 $f(X,\omega_i,\omega_r)\cos\theta_i\mathrm d\omega_i$
- 在数学上,简单表达为 $l(u)=e(u)+\int l(v)K(u,v)dv$
- 两个不同的位置分别用 $u,v$ 表示
- $K(u,v)$ 是从其他点的 $l(v)$ 反射到 $u$ 点上的能量系数

- unknown 不知道的项
算子
- 进一步简写成算子形式
- $L=E+KL$
- 物体辐射的能量 = 光源辐射的能量 + 辐射出来的能量被反射之后的能量
- $K$ 是反射操作符,可以把辐射出来的能量反射掉
- $E,L$ 是向量,$K$ 是矩阵
- 关于算子的严格定义,查看数学内容
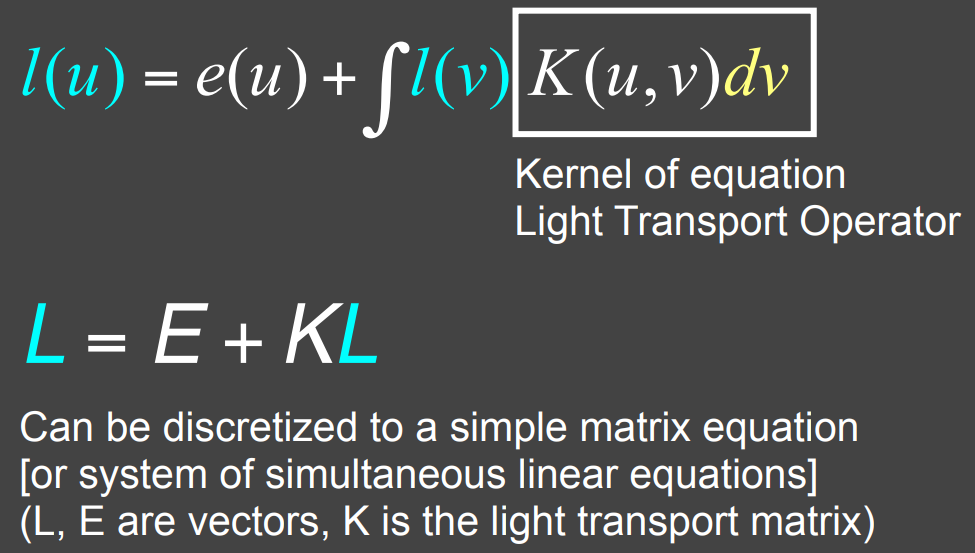
- $L=E+KL$
- 把算子方程进行数学展开
- 我们需要解 $L$(解渲染方程),得到任意一个方向能观测的能量,而通过简写,$L$ 是递归定义的
- 通过算子,可以求得 $L$ 的表达式(使用单位矩阵、分配律),并且算子有类似泰勒展开的性质
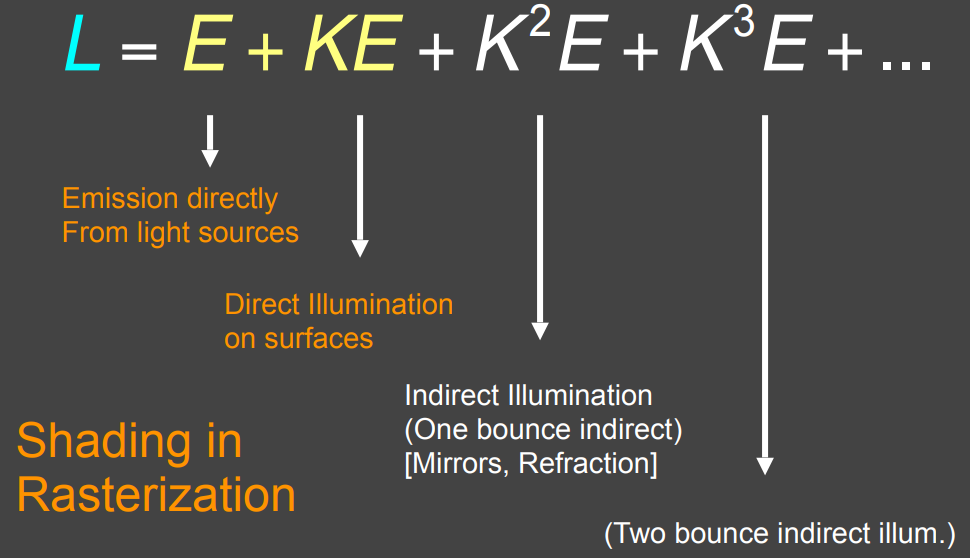
- 最终,写为 $L=E+KE+K^2E+…$,并且 $K$ 是反射操作符
- 理解为:可以把最后看到的一张图,分解为:
- 光线对弹射次数的一种分解
- 直接看到光源会看到 $E$
- + 光源辐射出来的能量经过一次反射后会看到 $KE$
- + 光源辐射出的能量经过两次反射,会看到 $K^2E$
- + …
- 光线对弹射次数的一种分解
全局光照
全局光照的概念
- 这样,引入了全局光照的概念
- 光线不弹射,就是光源
- 光线弹射一次,直接光照 direct illumination
- 光线弹射两次,间接光照 indirect illumination
- 所有不同的光线弹射次数的结果全部加起来,就是全局光照 global illumination
- 全局光照不仅是间接光照,而是直接光照、间接光照的集合
- 通过这个式子,再次理解光栅化 (图中橙色部分)
- 光栅化把物体投影到屏幕上,通过屏幕上任意一个着色点、物体位置、光源位置,可以做shading
- 光栅化 shading 做的就是直接光照
- 如 Blinn-Phong 模型计算环境光 + 漫反射 + 镜面反射,光线到物体到观测点,只有0次和1次的弹射
- 从间接光照之后,光栅化就难以计算了。这也是使用光线追踪的原因:更方便地计算多次反射后的光照
- 光栅化把物体投影到屏幕上,通过屏幕上任意一个着色点、物体位置、光源位置,可以做shading
全局光照的效果

- 观察图像
- 直接光照看不到的地方就是黑色。从一次间接光照开始(一次间接光照是光弹射两次),阴影部分变亮了
- 图片上方的玻璃灯,光线弹射次数少的时候,光线出不来。比如双层玻璃,光线需要两次才能弹进去
- 随着光线弹射次数再增多,画面之间的变化变小了。如果弹射无数次,图片会收敛到一个亮度,而不是一直变亮(过曝)
- 从观察上,图片变化越来越小了
- 从事实上,自然界中所有东西都是全局光照,没有越来越亮
- 能量守恒,能量是不会一直增加的
- 联想到摄像时,一直按快门就会过曝,这是因为对于能量,图形学一直考虑的是 flux,也就是单位时间。摄像在时间上积累了能量
- 也就是第一节课说的:画面越亮,全局光照做得越好
还剩一个问题:我们知道并理解了渲染方程,如何解全局光照的渲染方程?——路径追踪就是解渲染方程的一种方式。
Lecture 16 - Ray Tracing 4 (Monto Carlo Path Tracing)
1 - Probability Review
随机变量和概率(Random Variables & Probabilities)
期望(Expected Value)
- 不断取随机变量,求它们的平均

连续情况下的描述
- 概率密度函数(Probability Density/Distribution Function,PDF)
- PDF的概念在蒙特卡洛积分中会用到

除了随机变量的分布、期望,考虑随机变量的函数的分布、期望
依然是函数值×概率密度,积分起来

2 - Monte Carlo Integration
之前讲了 Radiometry;通过 radiance、irradiance 去解释反射问题,并得出了 reflection equation、rendering equation;通过算子把渲染方程拆成弹射形式,并定义 global illumination。
关于概率论相关知识,需要知道对于连续的概率分布函数,积分得到总体概率 1: $\int p(x)\text d x = 1$。
总览
Why
- 给定任何一个函数,需要求它的定积分
- 这个函数可能很复杂、写不出解析式;或者不关心解析式,因为定积分只要一个数作为结果,不定积分才关心解析式
- 使用数值方法,来求解这个定积分
How
- 回想黎曼积分:把定积分分为100份,每份取中点的函数值、计算矩形面积,最后相加
- 蒙特卡洛积分:直观上解释,考虑随机的采样方法
- 求 $\int_{b}^{a}f(x)\text dx$
- 取 $(a,b)$ 之间随意的值 $x$,计算它的函数值
- $f(x)$ 作为高、$b-a$ 作为宽,将矩形的面积作为定积分的近似值
- 重复采样多次,把所有的近似值平均起来,得到相对准确的结果
蒙特卡罗积分
定义
- 定积分:$\int_a^bf(x)\text dx$,求它的值是多少
- 随机变量:$X_i\sim p(x)$
- 蒙特卡洛近似:$F_N=\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}$
理解
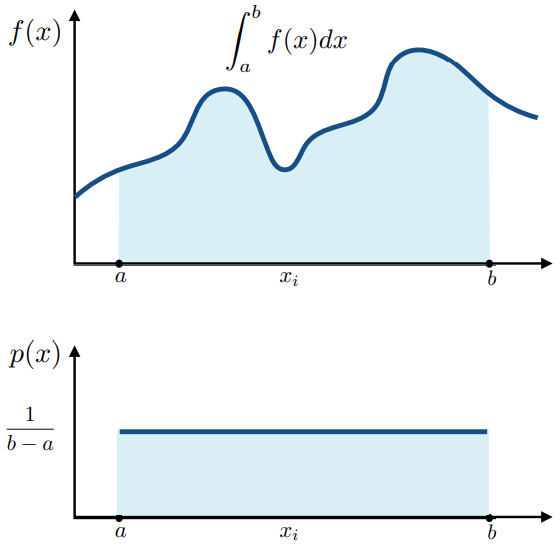
一个例子——均匀分布
- PDF:$p(X)=\frac{1}{b-a}$
- $F_N=\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}=\frac{b-a}{N}\sum_{i=1}^{N}f(X_i)$
- 用矩形的面积理解上式
- $b-a$ 是宽
- 高:该区间内取 $N$ 次函数值求平均
- 因此,当随机变量均匀采样,蒙特卡洛积分是合理的
一般地
对于任何积分 $\int_a^bf(x)dx=\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}$
结论:在积分域内,以一个 PDF 采样。采样出来的值 $f(X)$ 跟概率 $p(X)$ 相除,多次求平均,就能得到积分的值
只需知道采样对应的 PDF,就能近似计算定积分的值
notes
- 采样数量越多,近似结果越准
- 蒙特卡洛积分的要求:在 $X$ 上求积分,需要在 $X$ 上采样
3 - Monte Carlo Path Tracing
回想 Whitted-Style Ray Tracing
- Whitted-Style 光线追踪:

- 从摄像机发出光线,穿过每一个像素格子,射入场景中
- 不断弹射光线,在任何一个弹射位置,跟光源连一条 shadow ray 判断光源可见性,分别做着色,计算颜色值
- 当光线打到光滑物体,发生镜面反射 / 折射
- 当光线打到漫反射物体,光线停止
- 把每条光路所有点的着色加到像素的值里去
- 以上两个步骤,有不基于物理的部分:
- Whitted-Style 光线追踪无法处理 Glossy 物体:Glossy 表面不是镜面反射,而是把光线集中打到周围一块区域
- 打到漫反射物体,光线不应该停止,而应该向四面八方散射
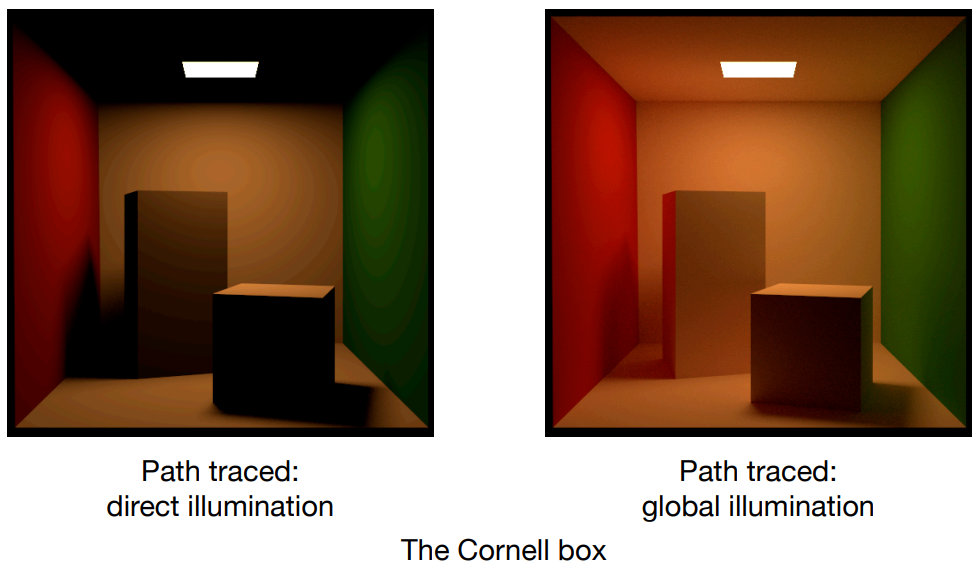
- 前面讲过,光栅化其实是全局光照中的直接光照。左图是直接光照,右图是加上间接光照、成为全局光照
- 使用全局光照后,观察天花板的全局光照,方块也展示出了 colour bleeding 现象(被墙“染色”)
- Whitted-Style 光线追踪无法处理 Glossy 物体:Glossy 表面不是镜面反射,而是把光线集中打到周围一块区域
- Whitted-Style Ray Tracing 是错的,渲染方程是对的:是完全按照物理量推导出来的
$L_o(p,\omega_o)=L_e(p,\omega_o) + \int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)\mathrm d\omega_i$
需要正确地解出渲染方程,有两个问题
- 考虑来自各方向的光照,需要计算半球的定积分
- 对于光线是直接还是反射而来,不做区分(递归)
它是定积分,采用蒙特卡洛方法来做
直接光照情况下的蒙特卡洛方法
问题
以一个简单情况为例,考虑一个着色点的直接光照是什么
- 场景有其他物体会挡住光,有一个大的面光源
- 考虑着色点接收各个方向 $\omega_i$ 的光线,观测方向 $\omega_o$,方向都向外
- 该点不发光
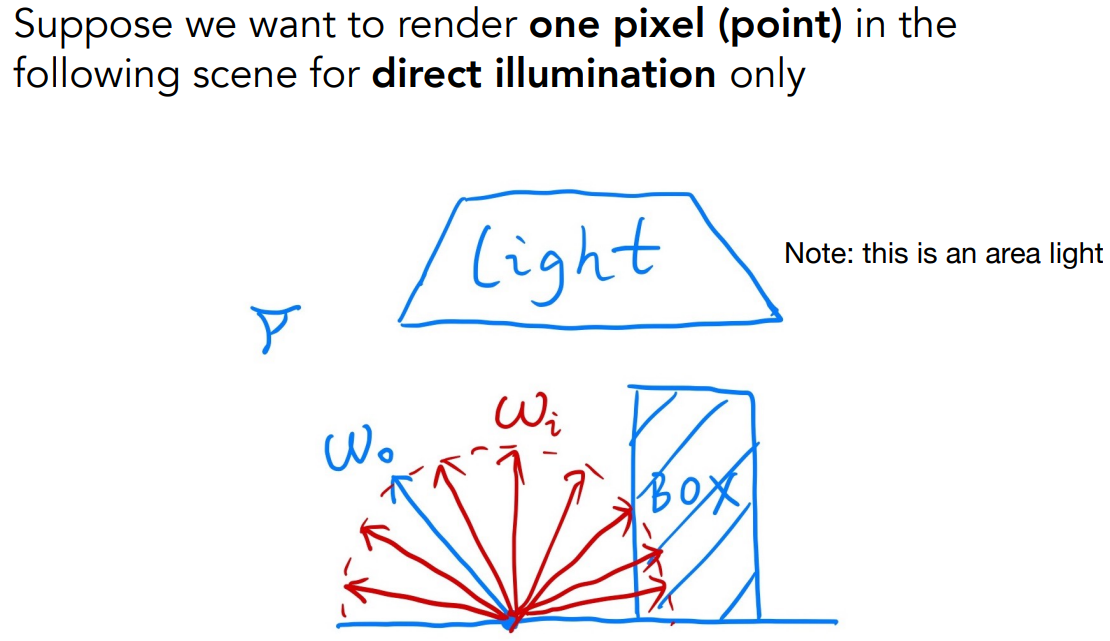
求解该点的渲染方程
- 该点的光照,就是各个方向的入射光 $L_i$ 经过 BRDF 反射到出射方向 $\omega_o$ 的光照之和
- 由于只考虑直接光照、不考虑多次反射,如果 $\omega_i$ 方向不是光源,$L_i =0$
- 使用蒙特卡洛方法:
- 求方向的积分,就在不同方向上采样
- 随机选一个方向,作为随机变量。需要知道采样的 PDF
蒙特卡洛方法
- $x$:方向,随机变量
- $f(x)$:$L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)$
- PDF(对半球的采样方法):均匀采样 $p(\omega_i)=1/2\pi$
- 立体角 $\Omega=\frac{A}{r^2}$
- 半球对应立体角 $2\pi$
- 近似渲染方程:
- 由此,写出只考虑直接光照情况下,任何点 $p$ 向 $\omega_o$ 方向的着色算法
shade(p, wo)
Randomly choose N directions wi ~ pdf # 对于p点,在N个入射方向采样
Lo = 0.0
for each wi # 对每一个方向取平均
Trace a ray r(p, wi) #建立入射方向wi到p点的光线
if r hit the light # 如果wi方向有光源,则计算该点求和式
Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
return Lo引入间接光照的光线追踪
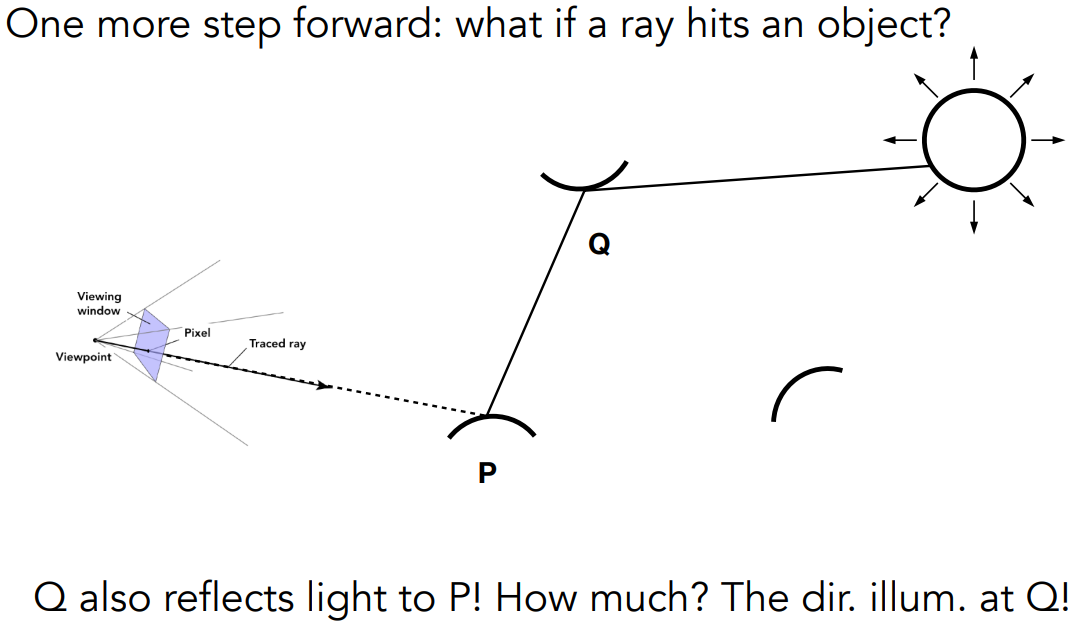
- 要算出在 Q 点反射多少 radiance 到 P 点,就是在 P 点观察 Q 点、计算 Q 点的直接光照
- 支持全局光照的路径追踪算法
shade(p, wo)
Randomly choose N directions wi ~ pdf
Lo = 0.0
for each wi
Trace a ray r(p, wi)
if r hit the light
Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
else if r hit an object at q
Lo += (1 / N) * shade(q, -wi) * f_r * cosine / pdf(wi) # 递归计算q点出射光
return Lo存在的问题
问题一:光线爆炸
- 此过程考虑在着色点上按 PDF 发出 N 个光线,如果打到物体再发出 N 个光线。光线弹射指数级递增
- 只有 N=1 时,光线数量才不会爆炸
shade(p, wo)
Randomly choose ONE directions wi ~ pdf # 在每个点只采样一次
Trace a ray r(p, wi) # 这条光线hit到什么就返回什么
if r hit the light
return L_i * f_r * cosine / pdf(wi)
else if r hit an object at q
return shade(q, -wi) * f_r * cosine / pdf(wi)- 用 N=1 来做蒙特卡洛积分,叫做 Path Tracing(路径追踪)
- 如果 N ≠ 1,叫做 Distributed Ray Tracing(分布式光线追踪),会产生光线爆炸
- 而 N = 1 就只剩一条光路,称为 Path
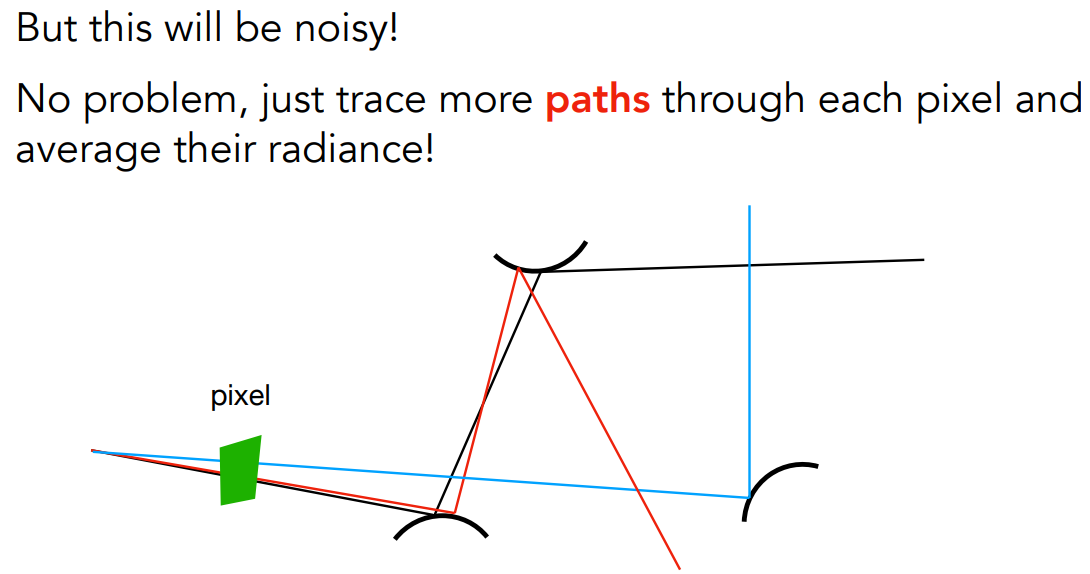
- 对于蒙特卡洛积分,N=1 的误差很高。然而,在成像问题上,ray tracing 是从摄像机穿过一个像素打出多条 path,分别计算其着色,再在多个 path 求平均。因此,对于每个像素发出的 path 数量够多,着色的误差会减小
- 每个 path 只向一个方向反射,形成了一条连接光源和摄像机的路径(path)
- 在一个像素内多次采样,path tracing 不仅解决了锯齿问题,而且解决了 texture mapping 中的走样问题
shade(p, wo)
Randomly choose ONE directions wi ~ pdf # 在每个反射点只采样一次
Trace a ray r(p, wi) # 这条光线hit到什么就返回什么
if r hit the light
return L_i * f_r * cosine / pdf(wi)
else if r hit an object at q
return shade(q, -wi) * f_r * cosine / pdf(wi)
ray_generation(camPos, pixel)
Uniformly choose N sample positions within the pixel # 每个像素均匀取采样点
pixel_radiance = 0.0
for each sample in the pixel
Shoot a ray r(camPos, cam_to_sample) # 对像素的采样点发出path
if r hit the scene at p
pixel_radiance += (1 / N) * shade(p, sample_to_cam) # 对这条path计算着色。像素所有采样点的结果取平均
return pixel_radiance- 代码中可以看到,path 由于只是一条光路,不需取平均;而对于像素的每个采样点计算出的 shading 结果取平均
问题二:递归结束
递归需要停止;然而在真实世界中,光线弹射次数也不会停,让递归停止意味着能量损失。
引入方法:Russian Roulette(RR,俄罗斯轮盘赌)
在之前的 path tracing 过程中,每个 shading point 稳定射出一条光线,并得到着色结果 $L_o$
引入一个概率 $P$
- 当生效时,着色结果变为 $L_o/P$
- 当概率 $1-P$ 时,得到着色结果为 $0$
这样,总体的期望没有改变:$E=P*(L_o/P)+(1-P)*0 = L_o$
在 shading point 上,不是稳定、而是以概率 $P$ 向外发出一条光线。最后返回的结果除以概率 $P$。这样,算法最终一定会停下来。
- 发出第 n 条光线的概率:$P+P^2+…+P^n=\frac{P(1-P^n)}{1-P}$
shade(p, wo)
Manually specify a probability P_RR
Randomly select ksi in a uniform dist. in [0, 1]
if(ksi > P_RR) return 0.0;
Randomly choose ONE directions wi ~ pdf
Trace a ray r(p, wi) # 这条光线hit到什么就返回什么
if r hit the light
return L_i * f_r * cosine / pdf(wi) / P_RR
else if r hit an object at q
return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR到此,就得到了正确的 path tracing 方法了。
4 - 对光源积分
之前方法的问题
目前的方法并不高效:改为 Path Tracing 后,平均化依赖于每个像素取的采样点个数 SPP。当 SPP 小,噪声高。如何在小 SPP 的情况下提高表现?
当前的 Monte Carlo Path Tracing,对于每个 shading point,使用均匀的 PDF $1/2\pi$,向四面八方采样(为了解决爆炸问题让 N=1,但采样的方向是随机的),也就是打出光线寻找光源。
光源大,需要打出的 path 就少;光源少,可能每 50000 根 path 才能打到光源一次,其他的 path 就浪费了。
思路:对于着色点,不再向四面八方采样,而是向光源采样。(蒙特卡洛积分是可以选择 PDF 的。当然此处换到光源上也是用均匀的 PDF)
对于图中场景,如果对面光源均匀积分,PDF是 $1/A$。然而之前提过,计算哪个区间的积分、就在哪里采样,此处求半球面的积分、在面光源上采样,不能直接用蒙特卡洛方法。
因此,需要把蒙特卡洛方程写成在光源表面上的积分。需要得知 $\text d\omega$ 和 $\text dA$ 之间的关系。
- $\text d\omega$ 是立体角,几何意义是该立体角在半径为 1 的球面上覆盖的面积
- 立体角的概念:面积 除以 距离平方
- $\text d\omega = \frac{dA\cos\theta’}{||x’-x||^2}$
重写蒙特卡洛渲染方程到光源的积分域:
到此,把问题转化为:在光源上进行采样,计算光源上的定积分。又可以使用蒙特卡洛方法了
- PDF:$1/A$
- $f(x)$:积分里面的式子
Sampling the Light
考虑最终看到的着色结果(radiance)的来源:
- 来自光源:对光源平均采样,进行求解。是直接光照,不涉及RR(直射,不需要让光停下)
- 来自其他非光源:用之前的方法做。是间接光照,进行RR(作为递归终点)

shade(p, wo)
# 计算直接光照
# Contribution from the light source. 对光源采样
Uniformly sample the light at x' (pdf_light = 1/A)
L_dir = L_i * f_r * cosθ * cosθ' / |x'-p|^2 / pdf_light
# 计算间接光照
# Contribution from other reflectors. 对半球采样,应用RR
L_indir = 0.0
Test Russian Roulette with probability P_RR
Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
Trace a ray r(p, wi)
if r hit a non-emitting object at q # 点q不再是光源,才计算。光源已经在L_dir算出来了
L_indir = shape(q, -wi) * f_r * cosθ / pdf_hemi / P_RR
return L_dir + L_indir一个小问题:
- 对于光源采样,考虑它对 shading point 的贡献,这里假设了光源没有被遮挡
- 在shading point跟光源采样点连一条线,查看是否遮挡即可
其他
到此,路径追踪已经讲完了。
- 对于点光源,路径追踪是很难处理的(难以对点光源采样,也难以做出直接光照),在此处不谈。可以把它做成一个很小的面积光源
- Path Tracing is indeed difficult
- 涉及到物理(辐射度量学)、概率、微积分(蒙特卡洛方法)、编码
- 对于本课程,Path Tracing 的“入门”的意义较轻,“现代”的意义较重
- Path Tracing 是几乎 100% 正确的算法,Path Tracing 可以做到照片级真实感

Ray Tracing 和 Path Tracing
- 以前说 Ray tracing,就是 Whitted-style Ray Tracing(光栅化的 shading 步骤)
- 现在说 Ray tracing,可以理解为:所有光线传播方法的大集合
- (Unidirectional & bidirectional) path tracing
- Photon mapping
- Metropolis light transport
- VCM / UPBP …
- 怎么生成一张图?现在通常回答:光栅化 or 光线追踪
过程中略过的问题——相关研究领域
- 怎样对半球均匀采样?generally,给定一个函数、一个 PDF,怎样进行采样?
- 蒙特卡洛积分可以用于任意 PDF,目前使用了均匀分布。
- 选择什么样的PDF是最好的?怎样针对性地对某个函数选择最好的采样方法。(importance sampling 重要性采样理论)
- 不同的随机数实现方法,能实现不扎堆的分布采样,性能更好
- low discrepancy sequences 低差异序列
- 能否把采样半球、采样光源两种方法结合起来,得到更好的效果?
- multiple importance sampling,MIS
- 从像素射出若干 path,为什么把它们平均起来就是像素的 radiance(是否要加权平均)?像素代表着什么?
- pixel reconstruction filter
- 每个像素的 radiance 算出来了,并不是一个颜色。并且 radiance 跟颜色不是线性对应的。如何进行映射?
- gamma correction 伽马矫正,HDR 图,curves,color space
Lecture 17 - Materials and Appearances
接下来的课程安排:17、18 是材质的内容,18 是前沿的做法;然后是 19 光场、20 颜色的专题知识;最后两节课是物理模拟 / 动画的入门内容。
有不同的材质,在不同的光照下,表现为不同的外观。光线追踪的渲染主要研究的是:不同的光照与不同的材质之间的作用方式。
在光线追踪中,材质 = BRDF,本节课就是讲各种不同材质的 BRDF。
1 - Materials
Material = BRDF
在 rendering equation 中,BRDF 定义了光从一个方向反射到另一个方向上的能量。BRDF 项决定光的反射方式,也就是物体表面的材质。
$L_o(p,\omega_o)=L_e(p,\omega_o) + \int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)\mathrm d\omega_i$
$f_r(\omega_i\rightarrow\omega_r)=\frac{\mathrm dL_r(\omega_r)}{\mathrm dE(\omega_i)}=\frac{\mathrm dL_r(\omega_r)}{L_i(\omega_i)\cos\theta_i\mathrm d\omega_i}$
本节课就是讲各种不同材质的 BRDF
不同的物体表面材质
漫反射材质
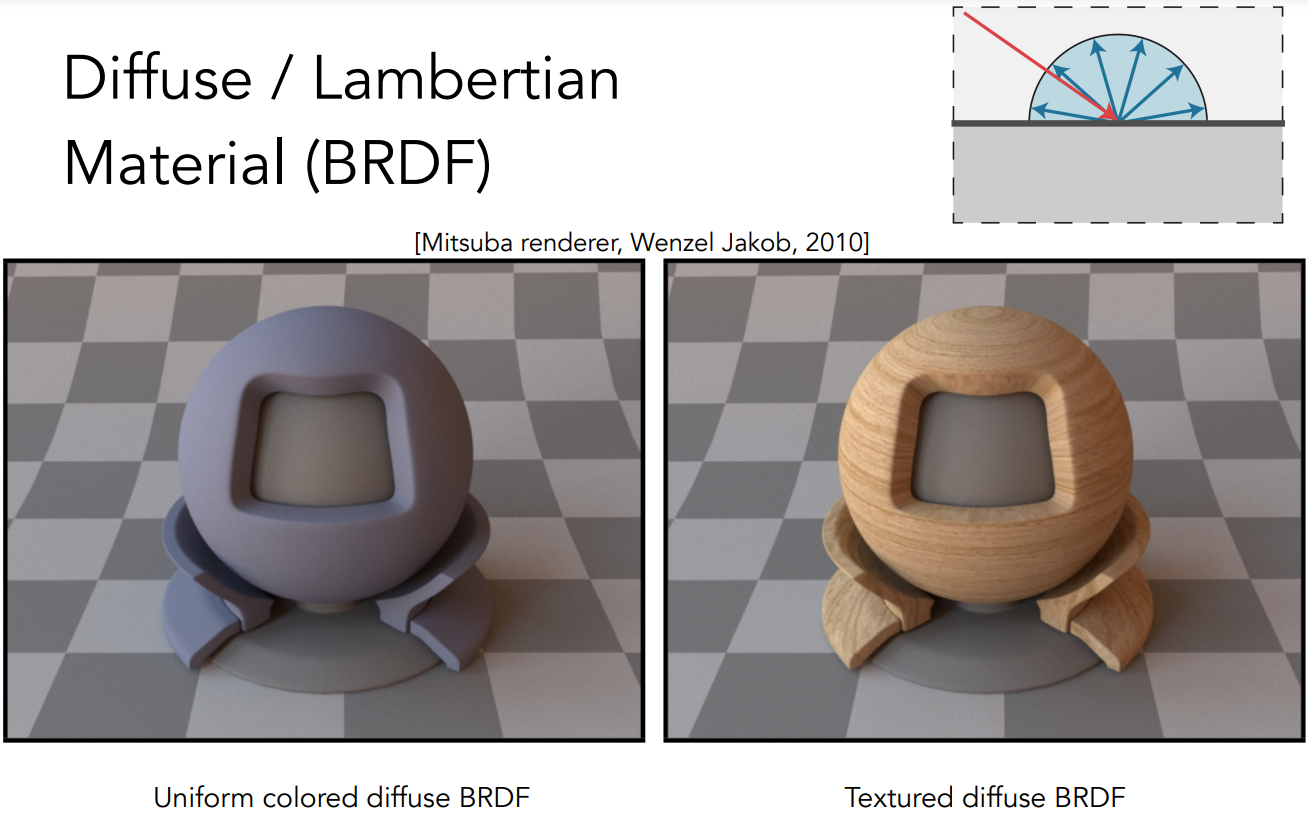
漫反射材质均匀向外发出光线
如果假设入射光也是 uniform 的,并且 shading point 不自发光,就可以从能量守恒的角度理解漫反射:接收各方向的均匀光线即 irradiance,把它们全部散射出去。从每个立体角考虑,入射 radiance=出射 radiance (因为入射和出射都是 uniform 的,并且能量守恒)
计算:
- 由于都是均匀的,假设入射光 $L_i(\omega_i)$ 是常数,BRDF $f_r$ 也是常数
- 半球上的立体角积分是 $2\pi$,cosine积分是 $\pi$
由于入射 radiance = 出射 radiance,$L_o=L_i$
得 $f_r=\frac{1}{\pi}$
定义一个漫反射的反射率 albedo,在0~1,可以引入不同颜色的 albedo。入射、出射方式依然是均匀的,但出射更少
Glossy 材质(不是很光滑的金属)
光线向一个方向集中反射
玻璃 / 水的材质
有反射也有折射
2 - 反射和折射,菲涅耳项
完美的镜面反射 Reflection
入射、出射方向沿着法线方向对称。可以通过这个关系,计算出射方向 $\omega_o$
回想 Blinn-Phong 模型,考虑出、入射方向的 half vector 跟法线方向是否接近,不考虑出射光和观测方向是否一致。这是因为如图所示,计算出射方向确实不简单,涉及到点乘操作。而计算half vector只需两个向量相加、normalize 即可。
所有的反射都能用 BRDF 来描述。镜面反射的 BRDF 是什么?这个值很难求,涉及到 delta 函数,此处不提。
折射 Refraction
右下角是 caustics 现象:海水反射阳光,海底的区域有几率同时被很多光线打到,表现为很亮。(这个现象 path tracing 不好做)
Snell’s Law 折射定律
相关概念
- 定义入射角 $\theta_i$,折射角 $\theta_t$
- 不同材质有不同的折射率 $\eta$,材质间的折射满足 $\eta_i\sin\theta_i=\eta_t\sin\theta_t$
- 入射、出射的方位角关系跟反射一样,都是正相反
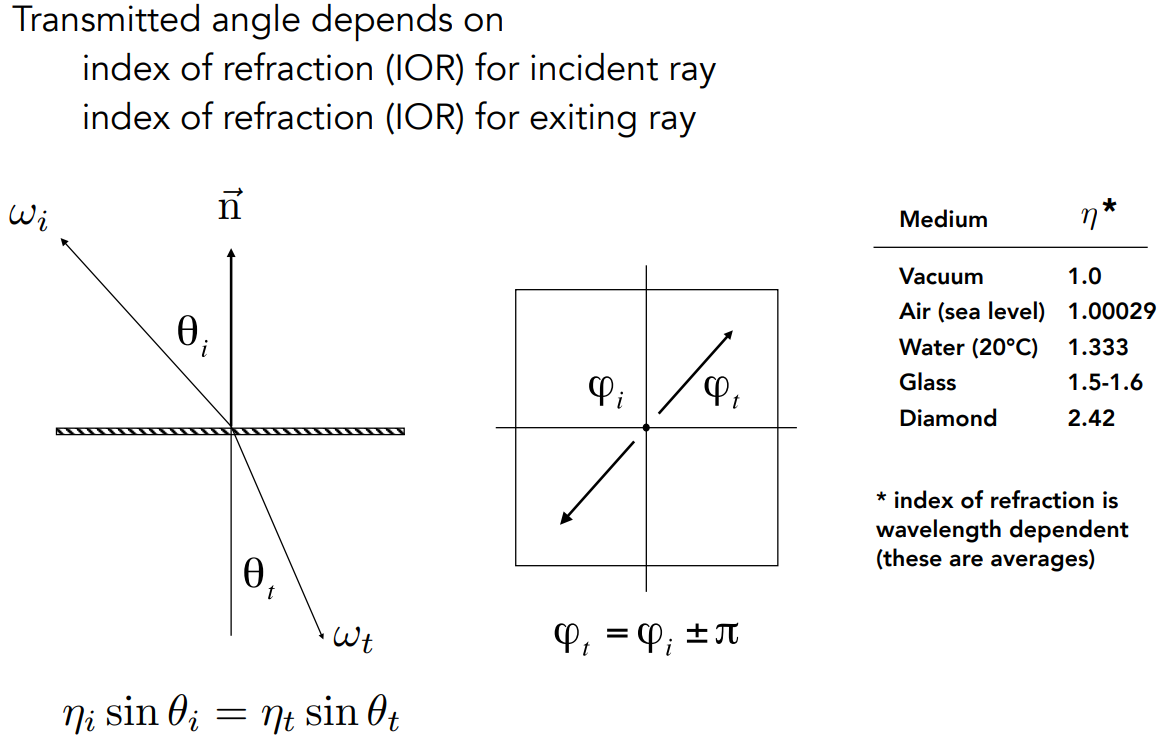
由折射定律,就能计算折射角 $\theta_t$
- 观察此式,当 $1-(\frac{\eta_i}{\eta_t})^2(1-\cos^2\theta_i)<0$ 时,公式是没有意义的,此式可以推出 $\frac{\eta_i}{\eta_t} > 1$、$\eta_i > \eta_t$
- 也就是说:光从某个介质来、到某个介质去,入射介质的折射率大于折射介质的折射率时,可能会出现没有折射的现象,称为全反射现象 (从稀疏的地方打到密的地方才折射,比如从空气入水)
- Snell’s Window / Circle:人在水底只能看到 97.2° 的锥形区域
- 考虑光线从水下射向大气,超过角度的光线都在水下发生全反射、不会进入空气中

- 为了把光线追踪做对,很多物理现象都需要考虑。对于之前作业里的球,球的性质是光线入射和反射有对称性,而对于复杂的物体,可能会在内部发生全反射,需要更细致的判断
关于折射的 BRDF,应该叫 BTDF。(BRDF 是描述物体表面的反射的。)通常,认为折射、反射都是散射 scatter,会把两者统称为 BSDF
菲涅耳项
反射和折射的性质——菲涅耳项(Fresnel Reflection / Term)
放在墙边的书,从高处看不到反射,接近平视时可以看到明显的反射
入射光(指观测方向)跟法线的角度,决定了有多少能量会被反射
光打到物体表面,有一部分反射、有一部分折射。通过菲涅耳项,可以解释有多少能量进行反射、有多少能量进行折射。
- 图中是折射率1.5的绝缘体
- 如图红线,入射光跟法向量垂直(跟物体表面平行),很多能量被反射;入射光跟物体表面垂直,很多能量被折射。
- 联想日常生活中,垂直看玻璃会看到窗外,平行看玻璃(坐车看前排的玻璃)会看到反射。
- 另外两条线反映极化性质,S、P是两个不同方向的偏振方向,渲染中不考虑
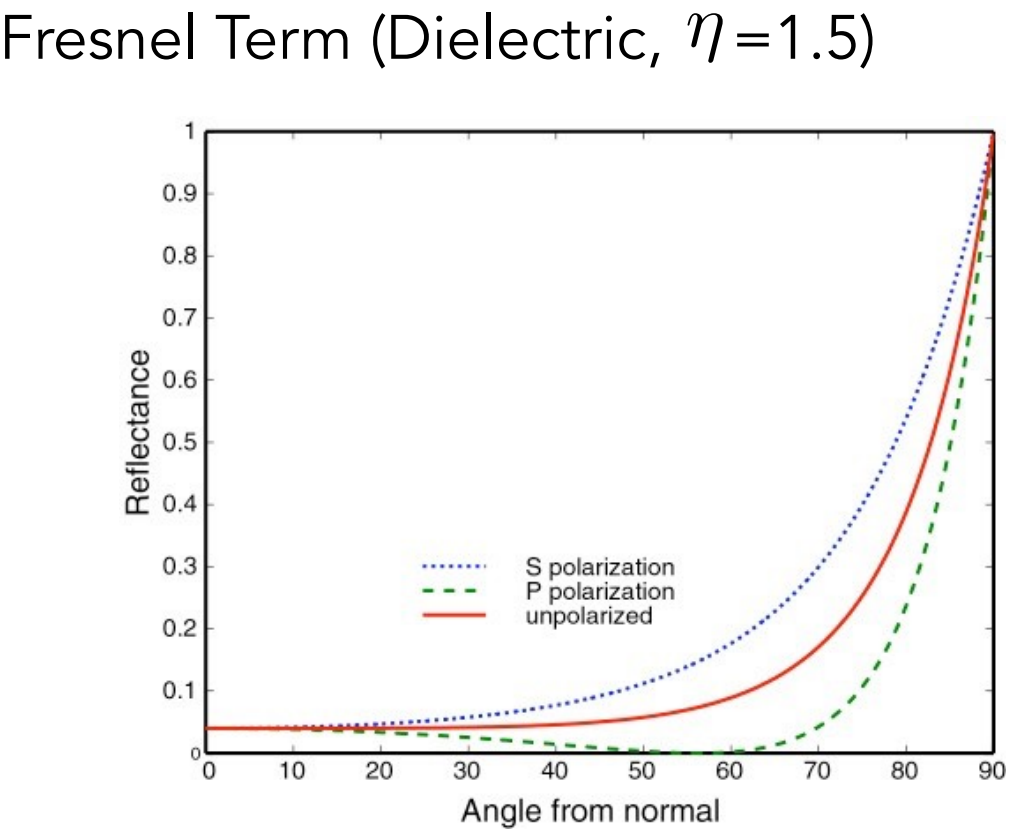
- 对于导体(金属),菲涅耳项跟绝缘体不一样
- 即使是垂直看,也是光线中的大部分被反射
- 因此使用铜、银制镜子,在所有情况下反射率都很高,而不用玻璃
- 理解:导体的折射率是一个复数
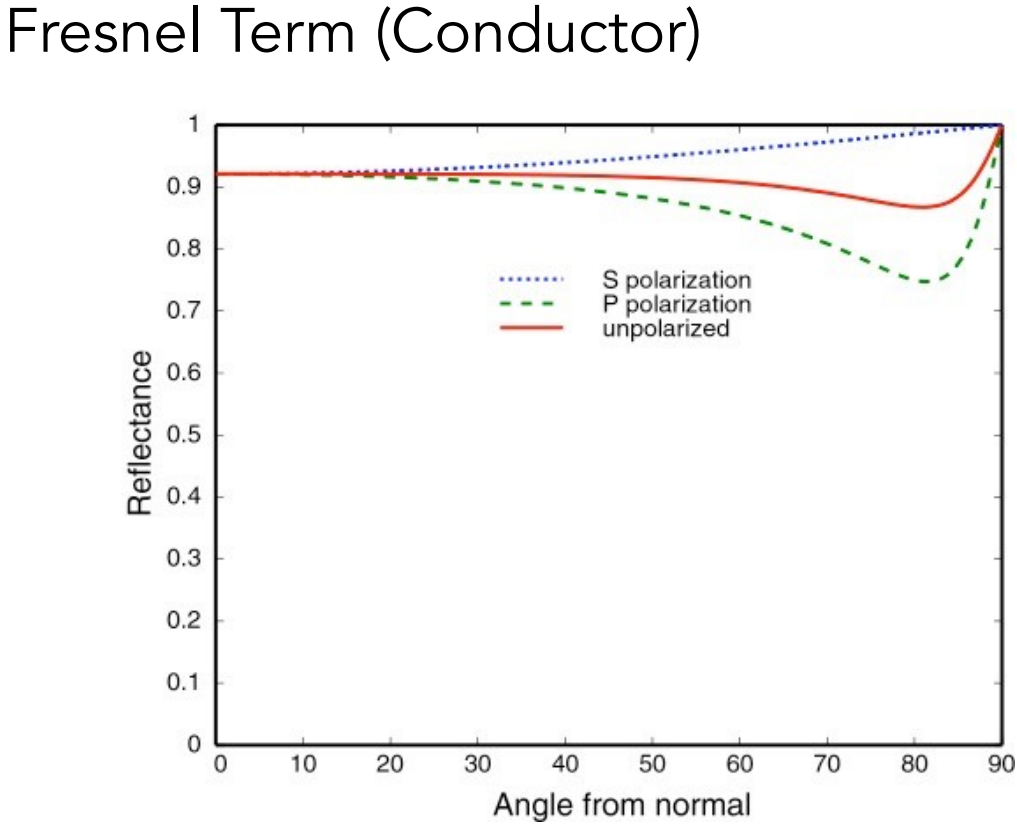
- 图中是折射率1.5的绝缘体
菲涅耳项的计算
- 可以精确计算反射出多少能量。可以看到,跟入射光跟法线的夹角有关,也跟介质有关
- 由于不关心极化,把S、P两个极求平均即可
- 也有简化方法:Schlick’s approximation,认为曲线在0°~90°的反射率一直是上升的过程
- 0°时为 $R_0$,90°为 $1$
- 只要不对材质的要求非常高,这就是图形学中被广泛应用的近似方法
- 如图为具体计算方法

3 - Microfacet Materials 微表面模型
定义一个真正的基于物理的材质
动机
- 基于一个假设:当离得足够远,在看向一个物体时,看不到微小的具体,只看到了最终对光的总体效应
- 图中,在空间站上看到地球陆地发生了完美的镜面反射,没有被细节的地形起伏所影响
微表面模型
假设物体表面是粗糙的,从近处可以看到 microsurface,但从远处看就是平的 macrosurface
Macroscale:flat & rough
- 从远处,看到平坦、粗糙的平面
- 从远处看到的是材质
Microscale:bumpy & specular
- 从近处看到凹凸不平的表面,并且每个表面的微元都认为是完全的镜面反射
- 每个微表面都有自己的法线
- 在物理上也是这样的:大量的微小镜子分布不规则,把光线均匀地反射到各个方向,形成漫反射
- 从近处看到的是几何
镜头拉远后,几何就变成材质。
微表面模型的 BRDF
由于每个微表面有自己的法线,可以研究每个微表面的法线分布
如果表面平滑,所有法线都跟整体平面法向量差不多,这就是 glossy 材质
- 如果全在一个方向,就是 镜面反射材质
如果表面粗糙,所有微表面朝向各不相同,形成 漫反射材质

发现:可以通过微表面的法线分布,表示不同的材质
- $h$:half vector
- $F(i, h)$:菲涅耳项
- 总共反射的能量
- $G(i,o,h)$:shadowing-masking
- 微表面之间可能会发生遮挡,有一些微表面会失去作用
- 当光线平着打到微平面,或者观测方向平行于微表面(grazing angle),容易发生这种现象
- 这一项用来修正这个现象
- $D(h)$:法线的分布
- 只有微表面的法线方向跟 half vector 完全一致(因为微表面是镜面反射),才能把入射方向反射到出射方向
- 把所有的微表面在该方向的法线方向做查询
- 这一项决定了的反射方法,决定了集中还是发散
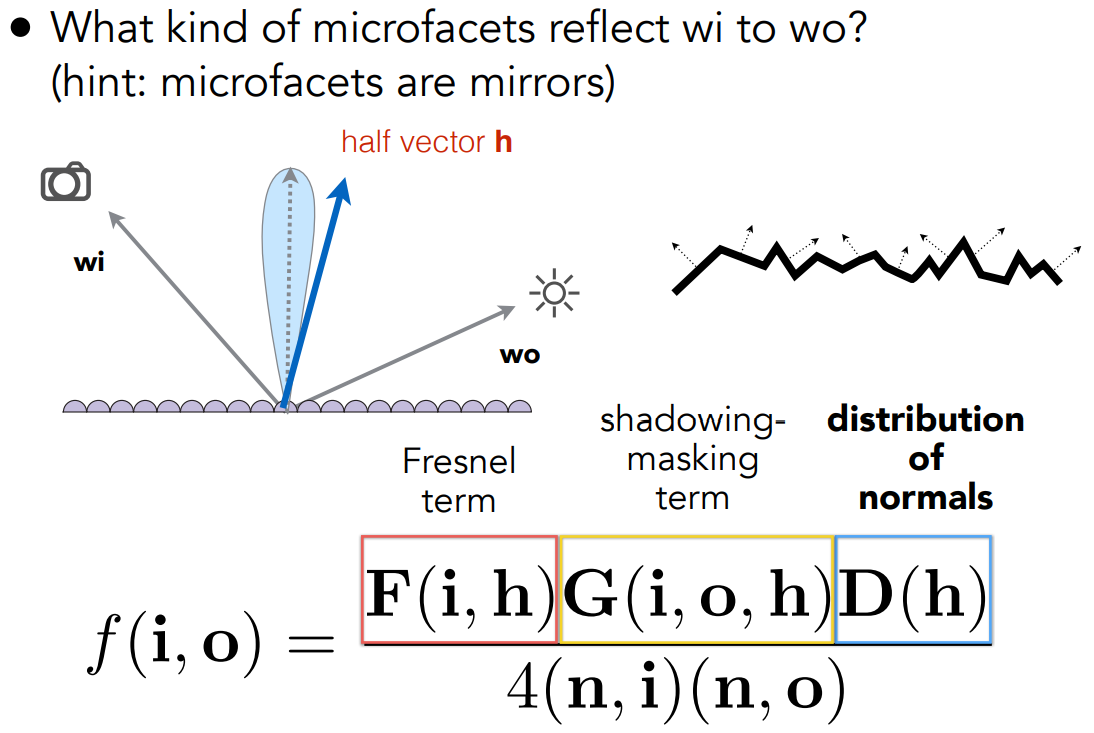
效果
微表面模型非常强大,可以渲染出很高质量的图片。是最近 state-of-art 的模型。
目前提到 PBR(Physics-based Rendering),就一定会使用微表面模型。
微表面模型是一个统称,有很多不同的模型,都遵循划分微表面这一套。
4 - 各向同性材质 Isotropic、各向异性材质 Anisotropic
拉丝金属反射的光:
区别:微表面的方向性
- 各向同性 Isotropic:微表面并不存在方向性,或者方向性很弱
- 各向异性 Anisotropic:水平和竖直完全不一样,微表面的法线分布有明确的方向性
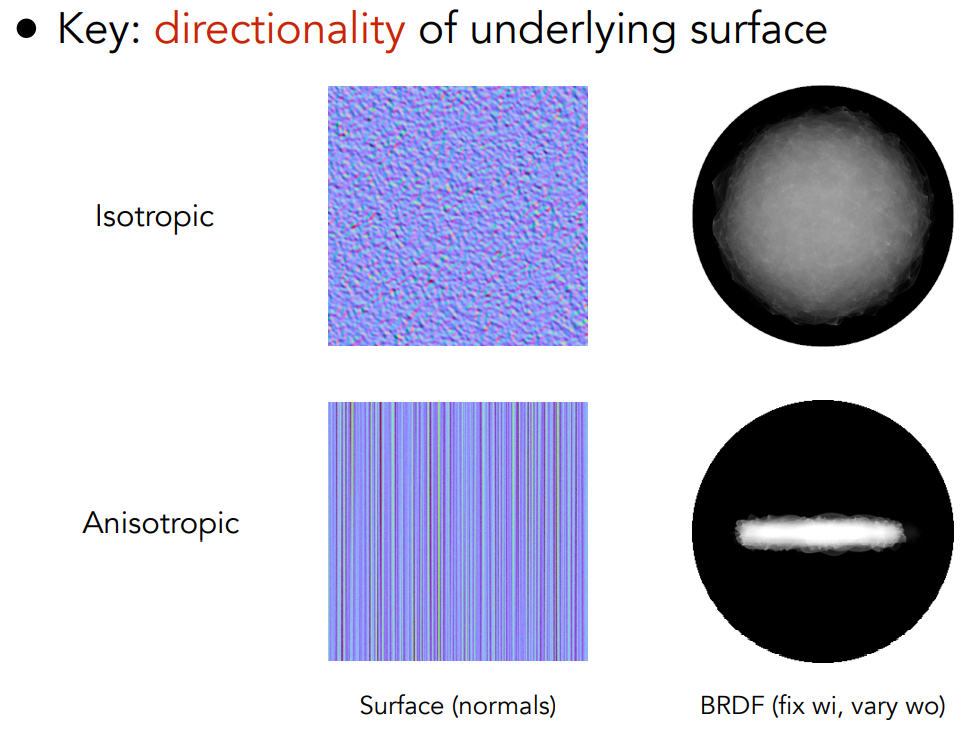
各向异性 BRDF
- 输入方向 $\theta_i,\phi_i$,输出方向 $\theta_r,\phi_r$,BRDF $f_r(\theta_i,\phi_i;\theta_r,\phi_r)$
- 如果不满足在相对方位角上旋转、得到相同的BRDF,就是各向异性的材质:$f_r(\theta_i,\phi_i;\theta_r,\phi_r) \ne f_r(\theta_i,\theta_r,\phi_r-\phi_i)$
- 入射、出射方向的相对方位角不变、绝对方位角改变,得出的BRDF不一样

- 生活中的各向异性:
- 锅的底部,一圈圈刷的
- 尼龙,上下叠起来
- 天鹅绒,把毛都刷到一边
5 - BRDF的若干性质
- Non-negativity 非负性
- BRDF 表示能量的分布,永远是非负的
- $f_r(\omega_i\rightarrow\omega_r)\ge0$
- Linearity 线性性质
- 对于 Blinn-Phong 模型,分成 difused、specular、ambiant,分别计算后把结果相加
- BRDF 本身也可以拆成很多块,可以分别计算并相加,得到的结果等同于整个做BRDF

- Reciprocity principle 可逆性
- 光路是可逆的:入射、出射方向互换,一定得到相同的BRDF值
- $f_r(\omega_r\rightarrow\omega_i)=f_r(\omega_i\rightarrow\omega_r)$
- Energy conservation 能量守恒
- BRDF 不会让能量变多
- 在 path tracing 时,经过无限次的光线弹射后,能量最终收敛,本质上就是能量守恒性质
- $\forall\omega_r\int_{H^2}f_r(\omega_i\rightarrow\omega_r)\cos\theta_i\mathrm d\omega_i\le 1$
- Isotropic vs. anisotropic 各向同性各向异性
- 如果各向同性,$f_r(\theta_i,\phi_i;\theta_r,\phi_r) = f_r(\theta_i,\theta_r,\phi_r-\phi_i)$
- 入射、出射方向的相对方位角不变,BRDF 就不变
- 原本四维的 BRDF,如果是各向同性材质,就是三维的
- 并且,由可逆性质,$f_r(\theta_i,\theta_r,\phi_r-\phi_i)=f_r(\theta_i,\theta_r,\phi_i-\phi_r)=f_r(\theta_i,\theta_r,|\phi_r-\phi_i|)$
- 相对方位角的正负也不必考虑了
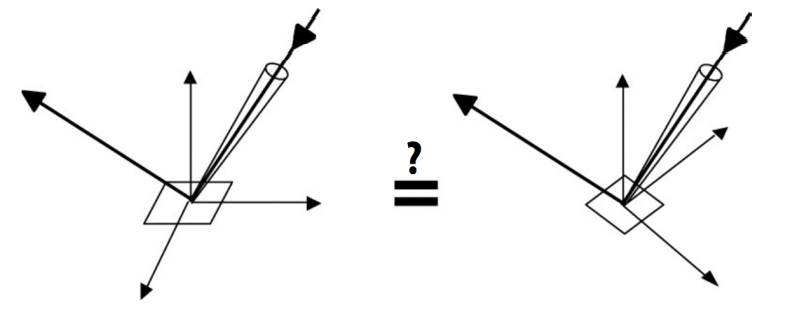
- 如果各向同性,$f_r(\theta_i,\phi_i;\theta_r,\phi_r) = f_r(\theta_i,\theta_r,\phi_r-\phi_i)$
6 - BRDF的测量与储存
BRDF 可以用各种基于物理的模型来描述(近似),但只有测出来的才是真正准确的 BRDF
- 推出的 BRDF 跟实际值有一定的差距
- 如果可以测量,就可以不去推模型了
怎么测?
- BRDF 就是两个方向的函数
- 盯着某一点看,改变入射方向(用灯在四面八方照),相机从四面八方拍,这样就覆盖了 BRDF 所有可能的输入、输出方向对
- 枚举所有入射、出射方向,测量四维的 BRDF(对于每个入射方向,让出射方向在球面上全走一遍,二维乘二维)
- 改进方法:
- 如果测各向同性的 BRDF,就把四维降成三维
- 如果考虑可逆性,减少一半的测量
- 设计更好的思路,不采样所有的方向对,测量某些样本、猜剩下的
测量完 BRDF 的存储要求:表示简洁、测量数据的精确表示、任意方向对的有效评估、重要采样的良好分布
一个 BRDF 数据库:MERL
测量了很多不同的材质(刚开始只有各向同性的,测量三维数据,即两个 $\theta$、相对方位角的绝对值)
最终结果存到三维数组里
每个材质做 90*90*180 次,需要进行压缩

Lecture 18 - Advanced Topics in Rendering
1 - Advanced Light Transport
总览
- Unbiased light transport methods 无偏光线传播方法
- Bidirectional path tracing (BDPT) 双向路径追踪
- Metropolis light transport (MLT)
- Biased light transport methods 有偏光线传播
- Photon mapping 光子映射
- Vertex connection and merging (VCM)
- Instant radiosity (VPL / many light methods) 实时辐射度
Biased vs. Unbiased Monte Carlo Estimators
蒙特卡洛方法的有偏和无偏
- An unbiased Monte Carlo technique does not have any systematic error
- The expected value of an unbiased estimator will always be the correct value, no matter how many samples are used
- 不管使用多少采样个数,蒙特卡洛方法估计的结果,期望是真实值,就是无偏的
- Otherwise, biased
- 估计出的值的期望跟最后要的值不一样,就是有偏的
- One special case, the expected value converges to the correct value as infinite #samples are used — consistent
- 特殊情况:
- 有偏:取多少样本,结果都是有偏的
- 在极限的定义下,取无限多的样本,得到的期望值会收敛到正确值
- 这种情况叫 consistent,也是有偏的
对于进一步有偏和无偏的理解(biased == blurry),在下面的光子映射方法中引出
方法一 Bidirectional path tracing (BDPT)
无偏方法之双向路径追踪
- 原来的光线追踪,利用光路的可逆性,从相机发射光线、判断跟物体相交,连接光源判断可见性
- BDPT:
- 从光源、摄像机生成两个子路径
- 把半路径的端点连起来,形成整条路径
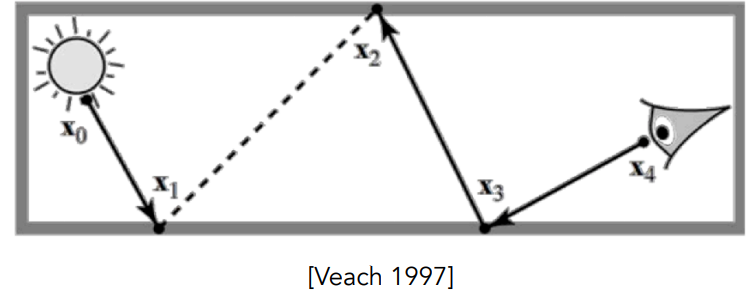
- 如图,光线打到墙壁全部进行漫反射。在这种情况下,使用仅从摄像机发出光线的单项路径追踪就难以计算
- BDPT 实现很难,运行慢

方法二 Metropolis light transport (MLT)
无偏方法之 MLT
- A Markov Chain Monte Carlo (MCMC) application
- 蒙特卡洛积分:在区间上均等概率采样,两次采样之间没有关系
- 可以用任意 PDF 采样一个函数,不知道用什么样的 PDF 是最合适的
- 实际上,用跟被积函数形状一致的采样函数 PDF,近似效果更好
- 用马尔科夫链(统计学上的采样工具):当前有一个样本,马尔科夫链可以生成跟这个样本靠近的下一个样本
- 蒙特卡洛积分中,可以用任意函数的形状的 PDF 采样
- 因此可以通过马尔科夫链采样 PDF,让 PDF 跟被积函数形状一致
- 蒙特卡洛积分:在区间上均等概率采样,两次采样之间没有关系
- 是一个局部的方法,给定任何路径,可以生成相似的路径
- 优点:特别适合做复杂光路的传播
- 找到一条光路作为 seed,可以在它周围不断找到更多
- 图中右侧是游泳池类似的现象,SDS-pass(specular - diffuse - specular)

- 缺点:
- 很难在理论上分析收敛速度,不知道何时停止(path tracing 是可以的,蒙特卡洛方法分析 variance)
- 所有操作都是局部的,相邻像素之间没有关系、收敛速度不同,导致图片看上去“脏”
- 不会作为渲染动画的方法,只渲染场景或单张图片(两帧之间像素收敛可能不统一)
方法三 Photon Mapping
有偏方法之光子映射
优点
- 特别适合渲染 caustics(光线聚焦产生的图案)
- 适合困难的光线如 SDS

做法:两步
- 第一步——photon tracing
- 从光源出发,向外辐射光子(光线),碰到物体就反射、折射,直到光子打到 Diffuse 的物体上,光子就停在那里
- 所有光子打完后,记录停留的位置
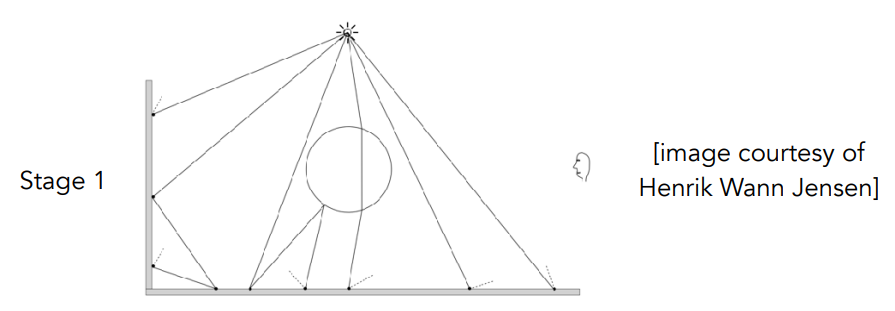
- 第二步——photon collection (final gathering)
- 从摄像机出发,打出若干 sub path,反射、直射,直到打到 Diffuse 的物体上
- 这样,光源光线(光子)和摄像机的光线都停留在物体表面上
- 计算 local density estimation
- 对任何着色点,取它最近的 n 个光子(nearest neighbor 问题,把光子组织成加速结构来解)
- 计算这些光子占据的着色点周围的面积、计算光子的密度
- 光子越集中的地方越亮
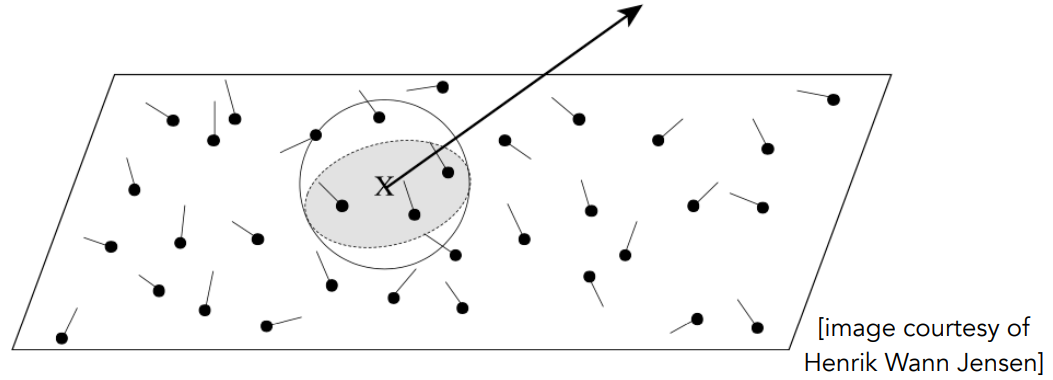
- 第一步——photon tracing
在计算过程中,如果找周围很少的光子数量,噪声会更大;如果找的很多,结果会模糊。用这个现象,分析为什么光子映射是有偏的方法,“biased” 意味着什么
- 从这个角度,光子映射可以理解为 variance(噪声)和 bias(模糊)之间的妥协
- photon collection 中,找的是数量(附近 n 个)而不是范围。因此对于密度的估计是不对的:
- 正确应该是微分来算 $\text dN/\text dA$,需要取着色点周围无限小的区域
- 但光子映射过程中是用实际数量来算 $\Delta N/\Delta A$
- 从极限的角度,如果光源打出特别多的光子,那么相同数量的光子覆盖的范围更小。在极限情况下 $\Delta A\rightarrow \text dA$
- 光子打出的数量无限多,就能得到正确的结果;光子打出的数量不够,结果会“糊”,也就是有 bias
- 因此,光子映射是有偏的方法,但是是一致(consistent)的方法
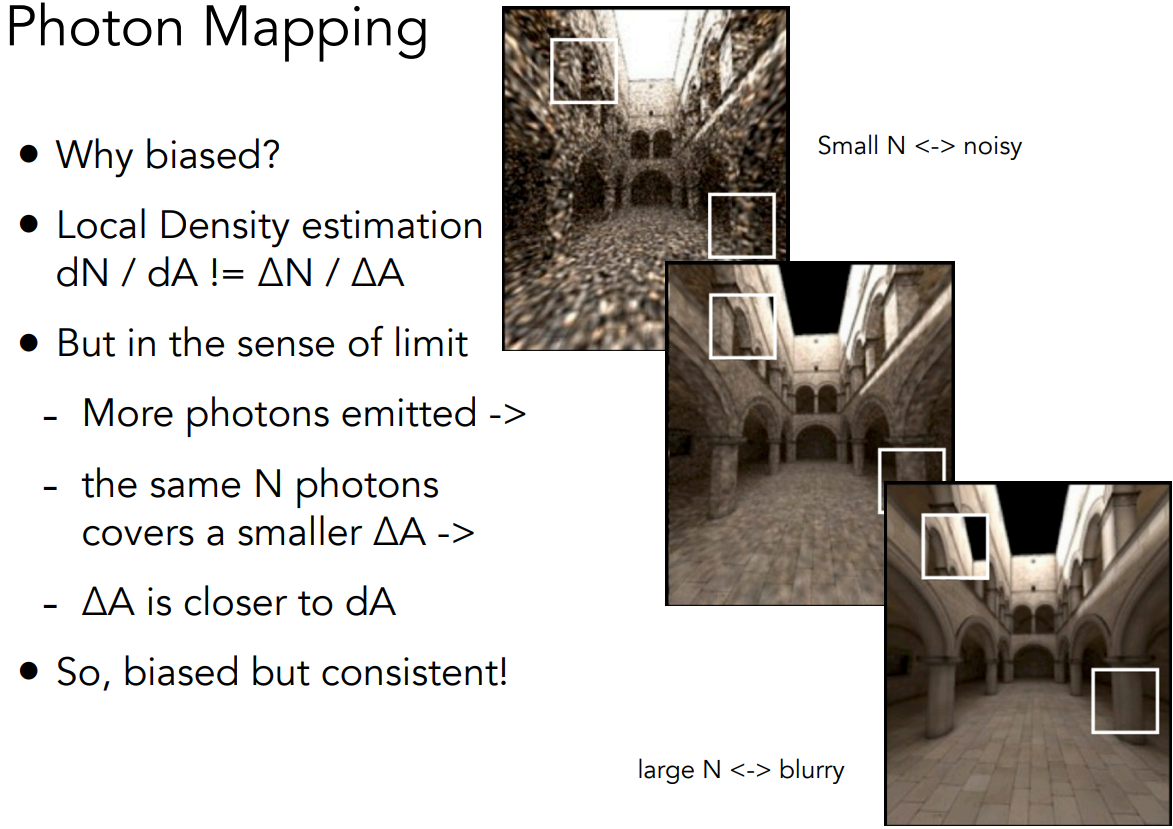
再看有偏和无偏
- Biased == blurry,得到的结果只要有模糊,就是有偏的
- Consistent 一致性意味着虽然有模糊,但只要样本足够多、最终会收敛到不模糊的结果
- 如果在 shading point 按固定小面积计算密度,得到的结果一定是有偏的、不一致的
- 在这种情况下,如果光子数量增多,范围内密度会增大,$\Delta A$ 不会趋近于 $\text dA$
方法四 Vertex connection and merging (VCM)
有偏方法之 VCM
双向路径追踪和光子映射的结合体,在电影中得到了广泛应用
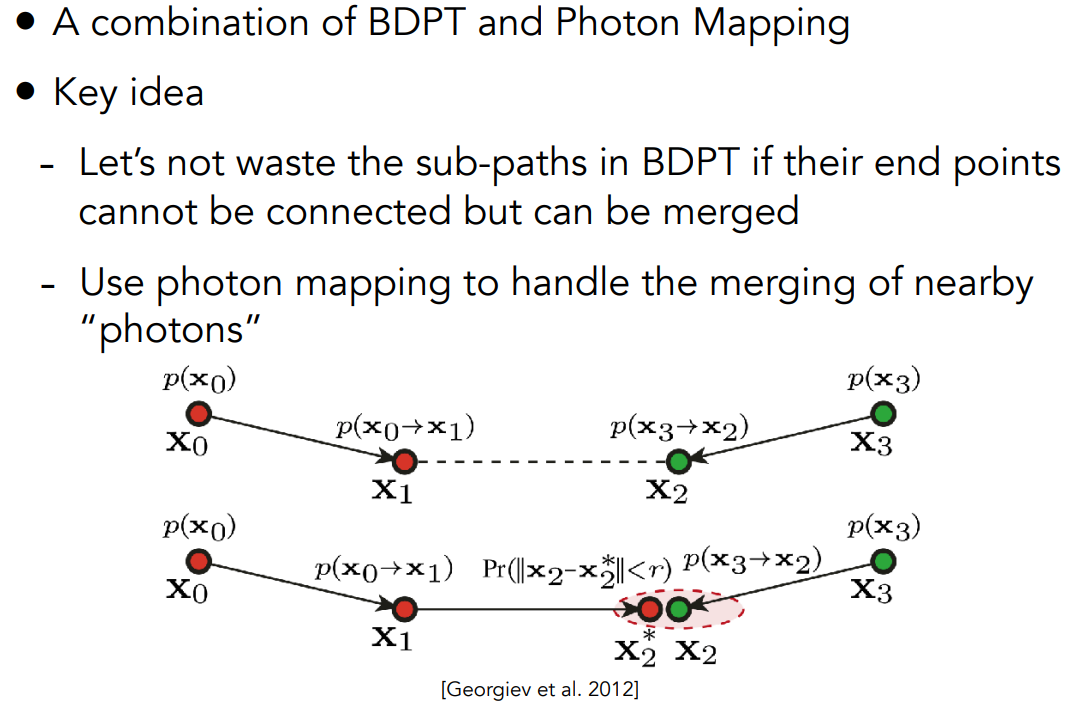
方法五 Instant radiosity (IR, VPL / many light methods)
其他光线传播方法之实时辐射度
在之前的光线传播中,并不区分光线是反射而来、还是自己发出来。把它们都作为 radiance。
实时辐射度利用了这种思想:已经被照亮的地方,都认为它们是光源,再用它们照亮其他地方。
从光源打出 light sub-paths ,停在哪里,这个地方就变成新的光源(VPL)
当看到某个点时,就用所有新的光源去照亮这个着色点
图中实际上是考虑了光线弹射两次,用直接光照的方法(都从光源发光)得到了间接光照的结果
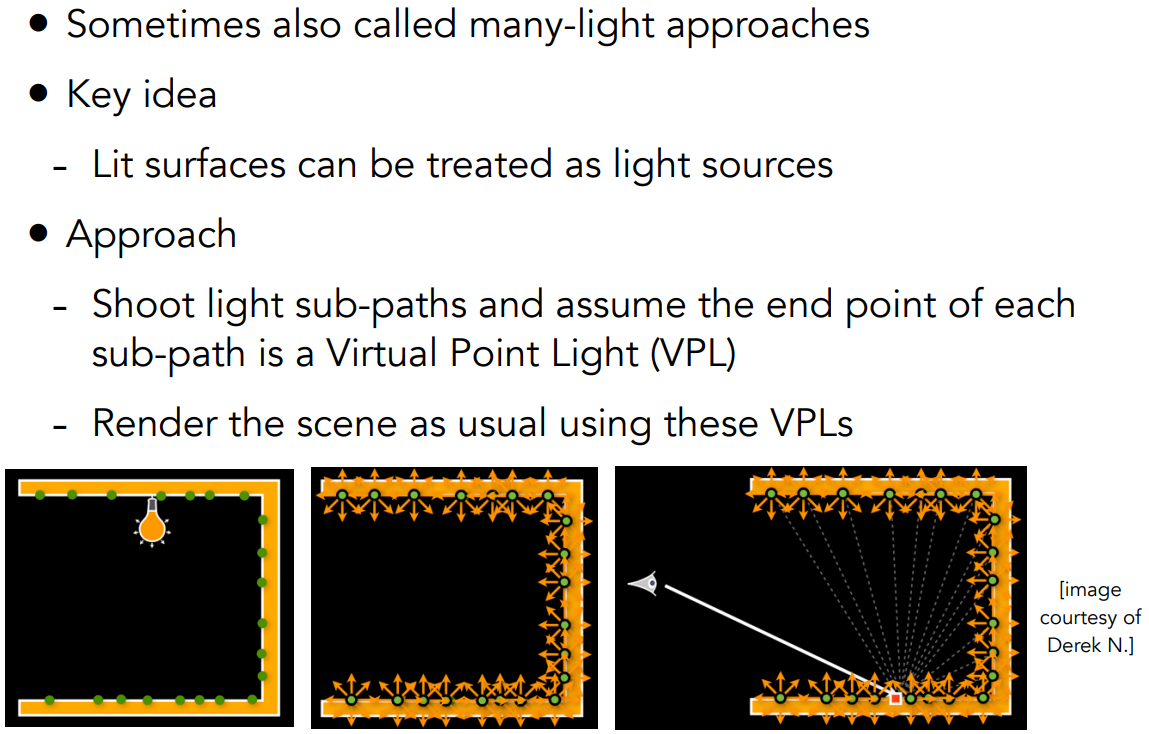
除了 IR,类似的 many-light rendering 也是一个研究领域
对于 Light Transport,至今没有一个完美的方法。很多公司还在使用 Path Tracing。
2 - Advanced Appearance Modeling
总览
Appearance = Material = BRDF
- Non-surface models
- Participating media
- Hair / fur / fiber (BCSDF)
- Granular material
- Surface models
- Translucent material (BSSRDF)
- Cloth
- Detailed material (non-statistical BRDF)
- Procedural appearance
是否是表面模型,取决于是否定义在物体表面上
2.1 - Non-surface models
模型一 Participating media
参与介质 / 散射介质定义在空间中(不只是一个表面),如雾、云。光线打进去,会被吸收、被散射。
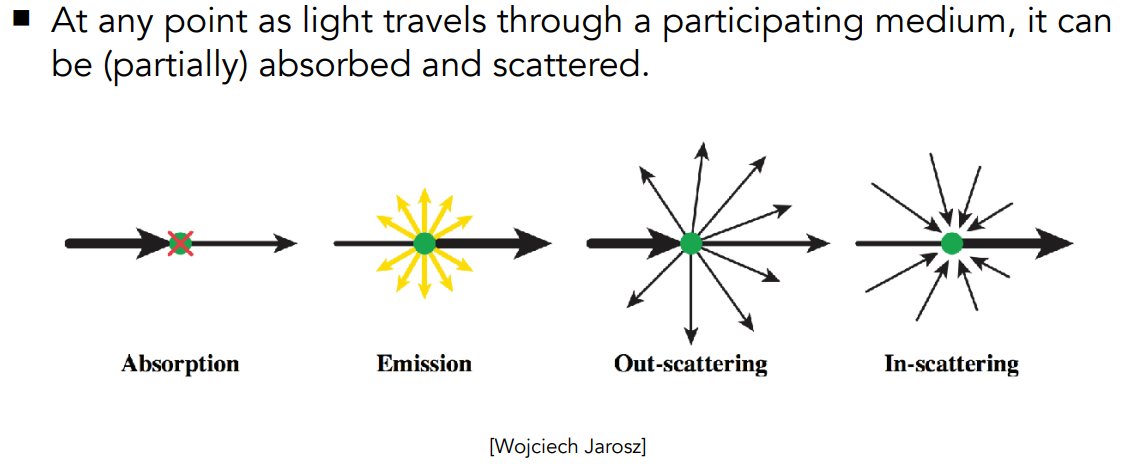
- 就像 Diffuse 表面会进行均匀散射,使用 Phase Function 来定义散射介质发生的散射
- 类比 BRDF 规定光线如何反射,Phase Function 规定了光线如何散射。具体的函数不再提
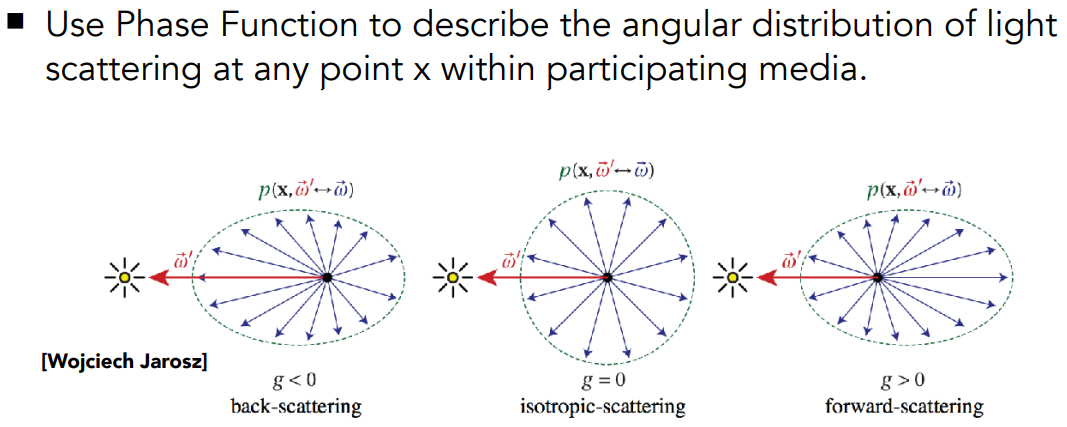
对于散射介质的渲染
假设光线身处其中,往某个方向走,能走多远决定了介质的吸收能力有多强,停下来后考虑把光线往哪个方向再次发射
由此,任何一个点都可能发生方向的改变
把散射点相连,找到一个 path,计算此路径对 shading 的贡献
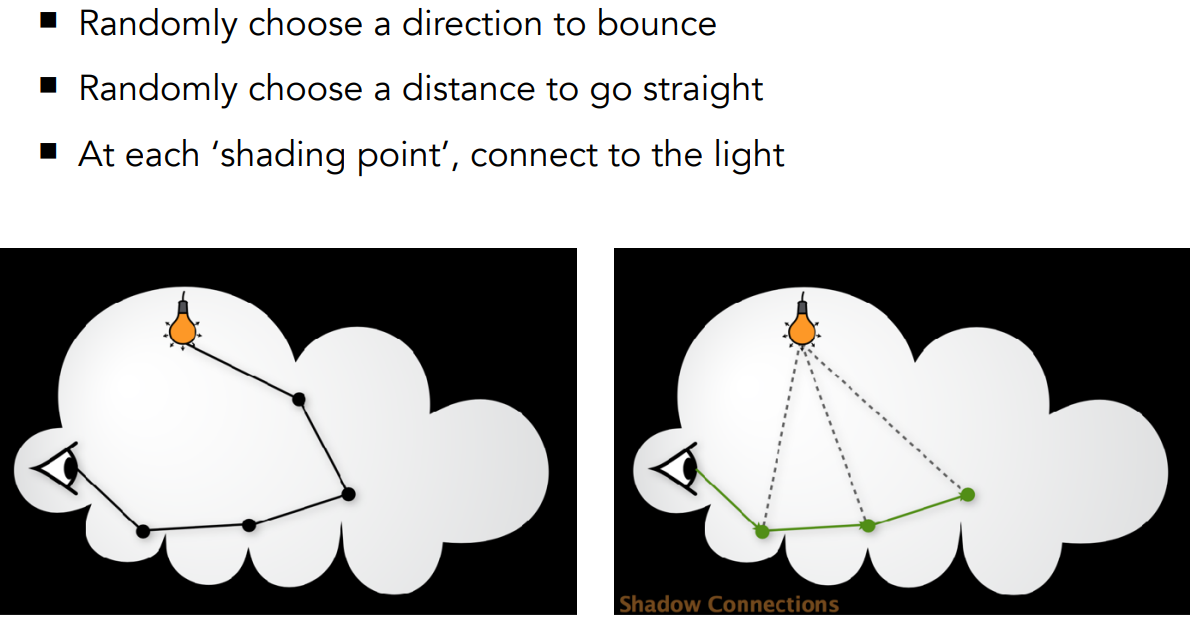
被用在电影(离线)、游戏(实时)中渲染烟和雾:
也不只是烟和雾。很多物体看上去是一个表面,实际上光线会进入其中并发生散射。比如展示的巧克力,或者手挡住闪光灯还能看到光线。光线会进入一个物体,可能发生比较少的散射。
模型二 Hair Appearance
头发会梳成一个面,也会单根表现出一些性质。对于头发的高光,分有色高光和无色高光(白色的)。
- 如图,头发整体有一个高光,同时每根头发也各不同

从研究头发开始,人们广泛采用一个简单的模型:Kajiya-Kay Model
- 一根光线打到一个圆柱上,考虑每根头发会把光线散射成一个圆锥。约等于 Diffuse + Specular
- 使用这种模型渲染的头发看上去不太合理
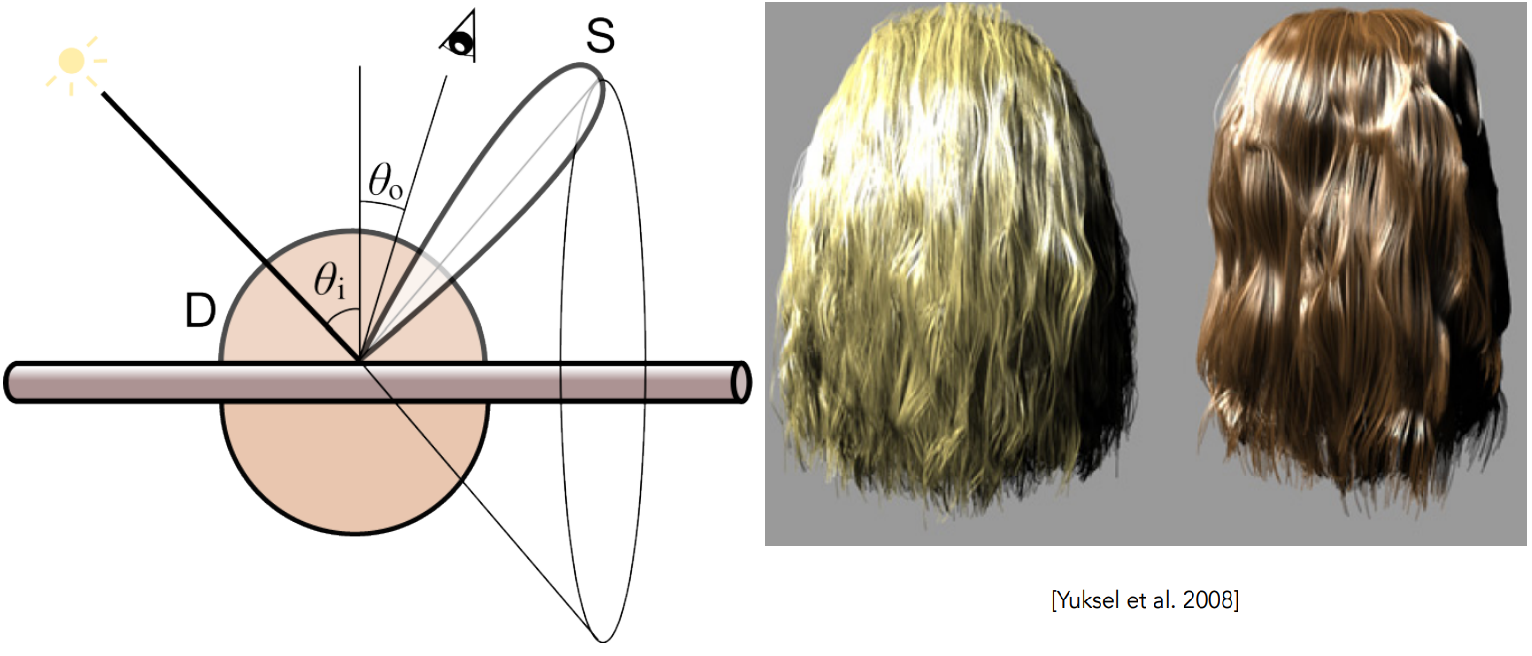
后面,使用一个复杂的模型:Marschner Model
- 考虑光线打到圆柱,有一部分会被直接反射;也有一部分会穿进头发,发生折射,再穿出去
- 记反射是 R,穿进穿出一个表面是 T。光线穿过头发就是 TT,还有 TRT(穿透、内部反射、穿透回去)
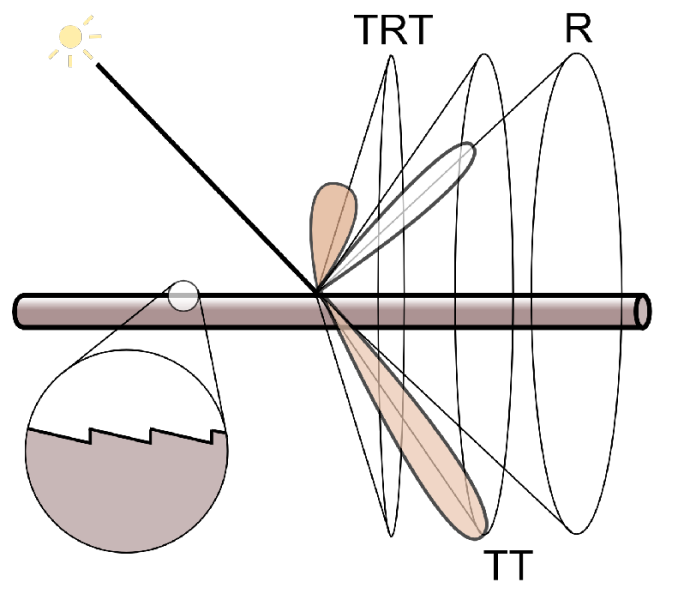
- 具体来说,头发表示为一个玻璃柱。分 cuticle(表皮)、cortex(内部),cortex 代表头发的颜色,模拟了光线进入头发、会被部分吸收的现象,黑发吸收得多,金发吸收得少
- Marschner 模型模拟了三种圆柱的作用:R,TT,TRT
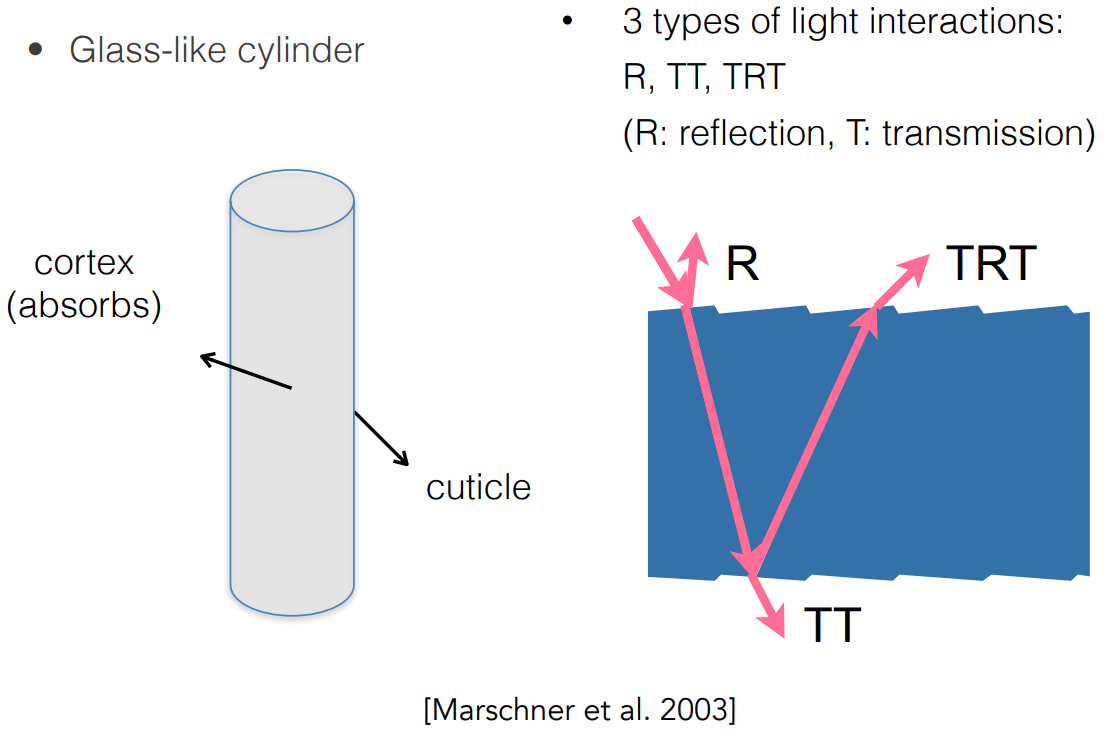
- 头发有很多,光线会发生多次散射。头发的渲染是困难的
此外,对于动物,使用人的头发的渲染方法,得不出真实的效果。

在生物上,人和动物的毛发除了 cuticle、cortex,还有中间的 Medulla(髓质),髓质内部非常复杂,光线打到髓质会像进入散射介质一样、被打到四面八方。动物的髓质比人的髓质大很多,光线更容易发生散射
因此,Marschner Model 的玻璃柱模型忽略髓质是不好的。对于人类头发,加入髓质的模型也会提高渲染质量
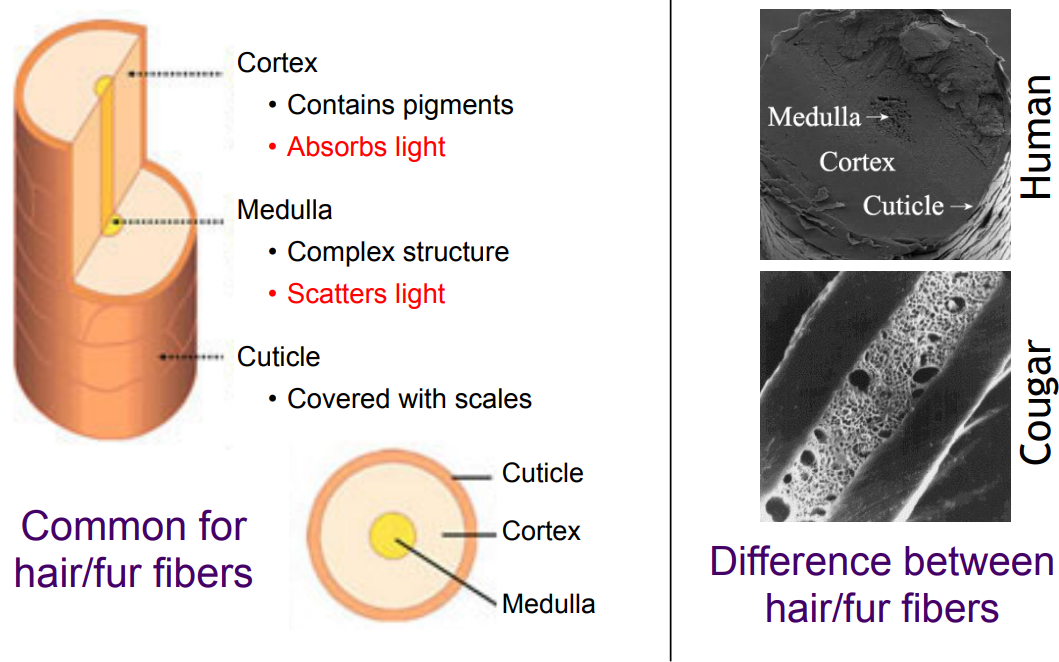
加入髓质,定义 Double Cylinder Model
在圆柱模型中间加一个圆柱,来模拟Medulla。光线打到Medulla会进行散射,记为s
同样,定义五种光线模型,具体如图
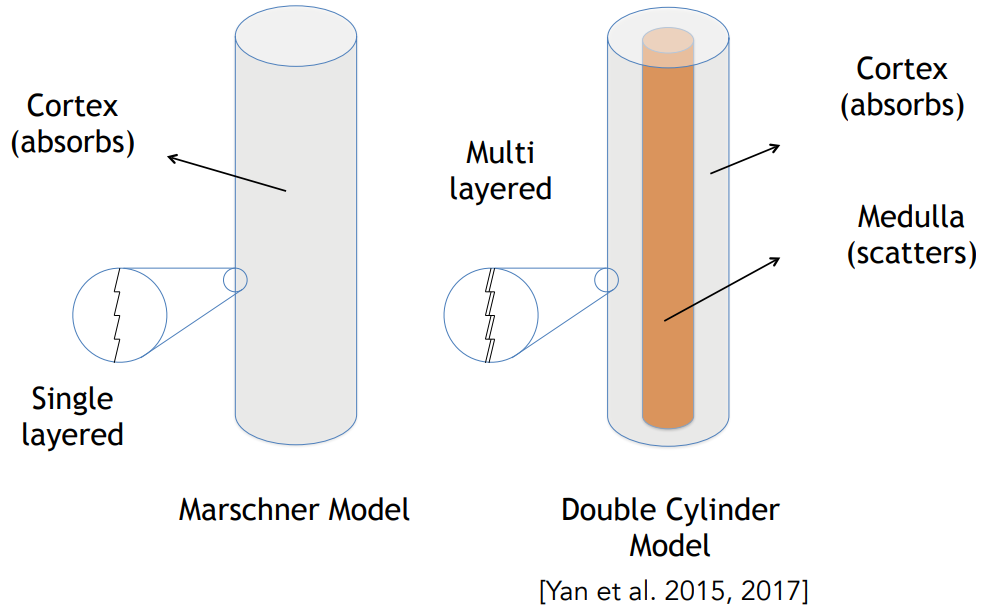
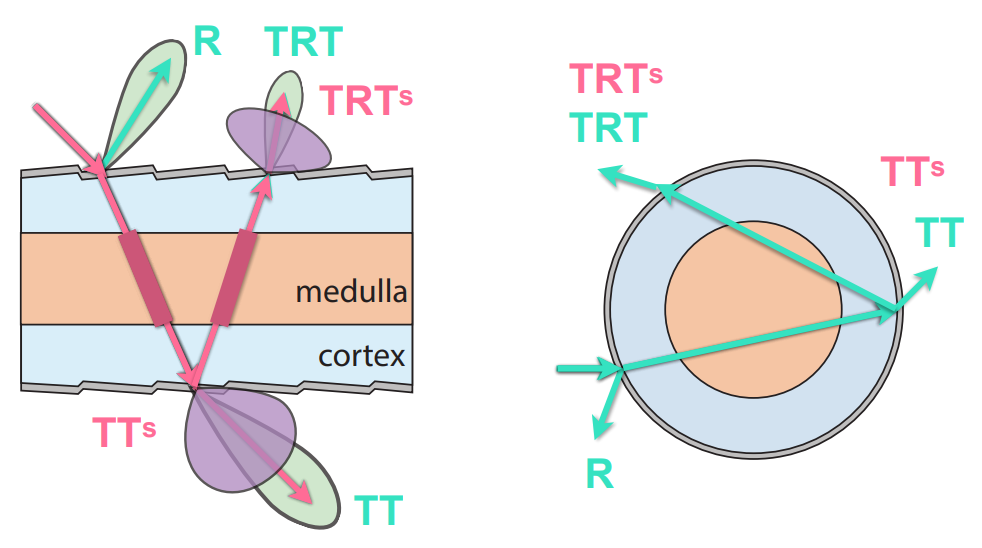

模型三 Granular Material
似颗粒状的,一堆小东西形成的模型,如沙子、香料等

- 如果渲染每个颗粒,计算量巨大。可以简化整个模型,认为每一个单元上由很多石子构成,各部分成分有多少
- Granular 模型的计算量依然巨大,至今没有比较好地应用
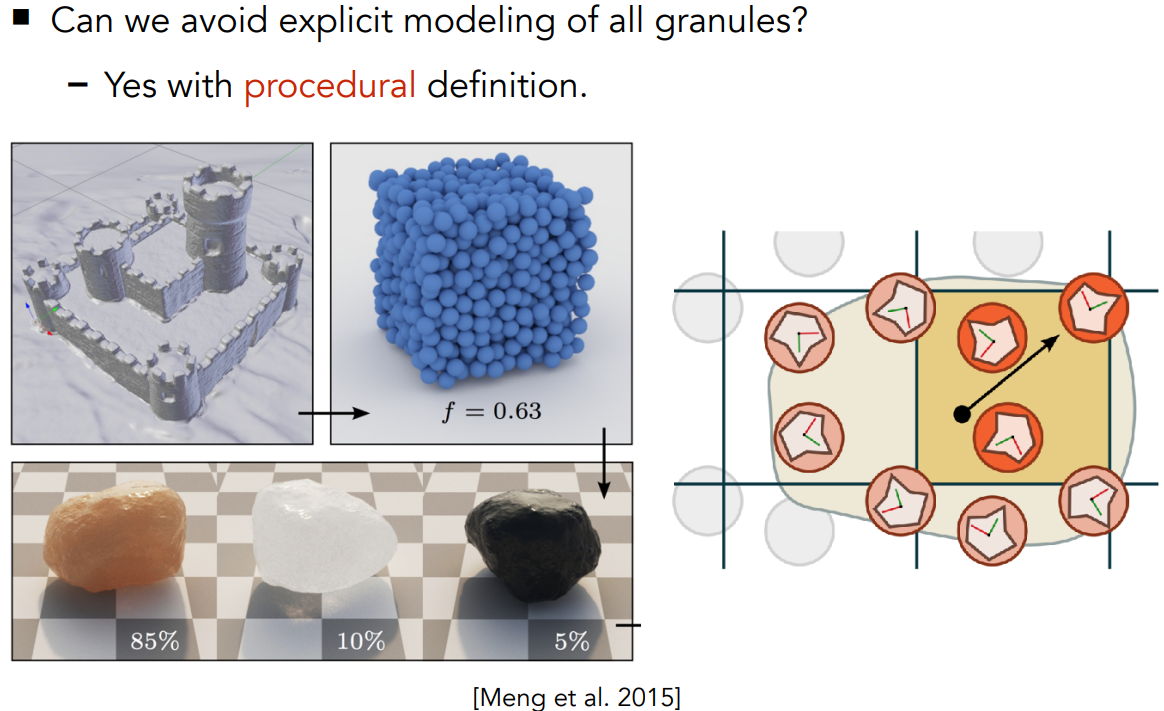
2.2 - Surface Models 表面模型
模型一 Translucent Material
以玉石、水母为代表的透光性材质(Semi-transparent 半透明,Translucent 透光性),光线在物体内部发生一些散射,然后再射出物体。
把这种现象称为:Subsurface Scattering 次表面散射
次表面散射可以看作 BRDF 的延申,定义 BSSRDF
- BRDF 所有的作用都发生在一个点上,定义光线打到一个点上、从这个点反射出去的能量;BSSRDF 光线进入一个点,可以从很多个地方出去
- BSSRDF 不仅考虑任何点、接收任何方向的光照,而且要考虑不同点对于某个方向射出能量的贡献。因此,不仅对半球积分,也对面积积分
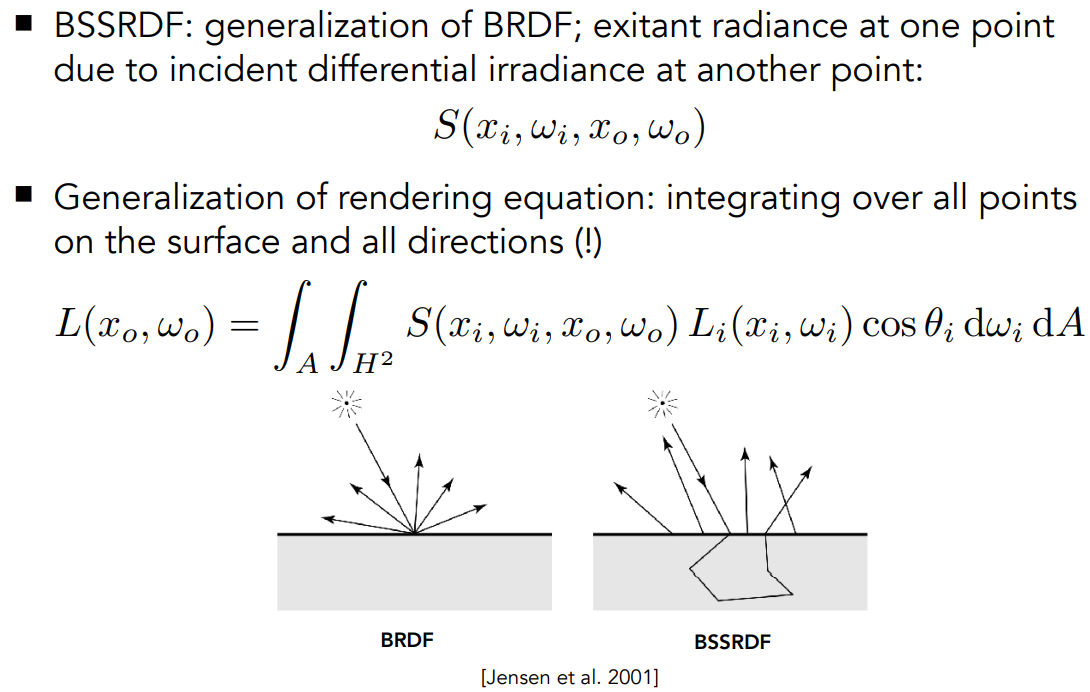
这样计算很复杂,使用近似方法:Dipole Approximation
- 用物体内部、外部两个光源照亮物体着色点区域,就很像次表面反射的结果
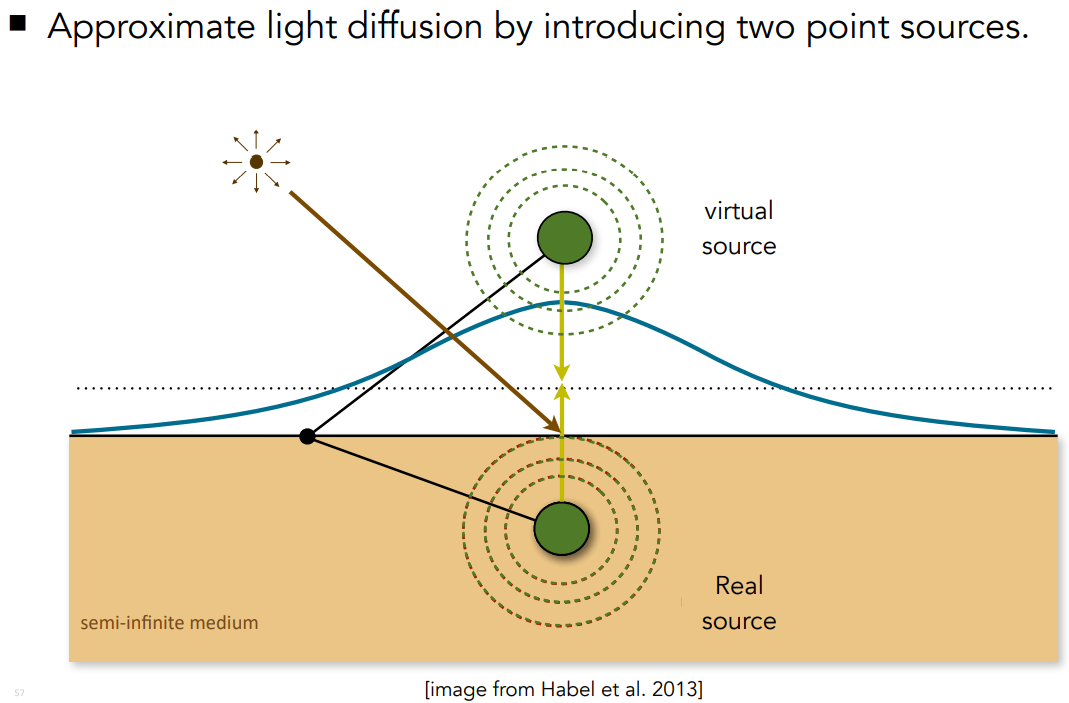
BSSRDF模拟了真实世界中,光线进入物体、在局部进行散射的现象,尤其是在渲染人的皮肤时效果很好
模型二 Cloth
布料:由一系列缠绕的纤维构成,缠绕有不同的层级
- 最基础的纤维(一根羊毛、化纤)经过缠绕,可以得到不同的股 Ply
- 不同的股再缠绕,会形成线 Yarn
- 有了线,可以做成布(编织和纺织)
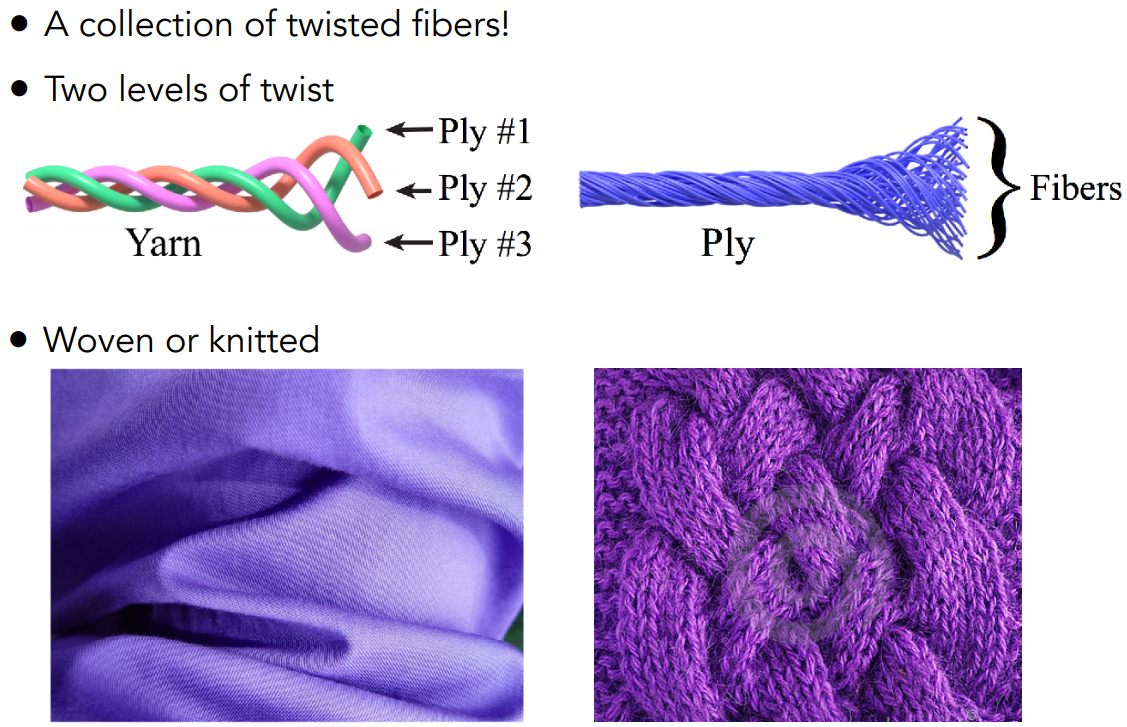
对于这类布的渲染,光线肯定跟纤维的缠绕方式有关。
第一种方法,如果认为布料就是物体表面,对于布料的渲染,通过给定任意的编制图案,计算出最终的光照结果(一个 BRDF 的关系) 。
然而,(前面的各向异性提过)对于天鹅绒等所有毛发向外的布料,正常情况下不是一个平面,不能用 BRDF 来表示。
因此,另一种方法是:认为织物是空间中分布的体积,当作反射介质来做
- 把它划分成细小的格子,每个格子内知道纤维的分布,能计算光线的吸收和散射
- 这样把渲染布料(面),转化成渲染云、烟、雾等反射介质(体积)的问题
- 计算量非常大,但结果更好
还有一种方法:布料是由一根根的实际纤维组成的,直接暴力渲染每一根纤维(当作头发)
直到今天,散射介质、实际纤维、物体表面,这三种布料渲染的方法都有人使用。
模型三 Detailed Appearance
动机:在渲染时,往往得到过于完美的结果,带来不真实感。在生活中有各种各样的细节,比如划痕等。
回顾:微表面模型
微表面模型最重要的是微表面的法线分布,在描述分布时用比较简单的模型(如正态分布),导致看上去结果缺少细节
可以通过不同方法(高度贴图,加亮片)定义细节,但渲染它们非常困难,因为微表面是镜面,从摄像机 / 光源射出的光线,经过镜面反射,很难打到光源/摄像机上去,渲染高光需要很长时间
在这里,考虑一个像素会覆盖很多的微表面,如果能算出一个小范围内的微表面法线分布,就能替代光滑的分布,并用在微表面模型里
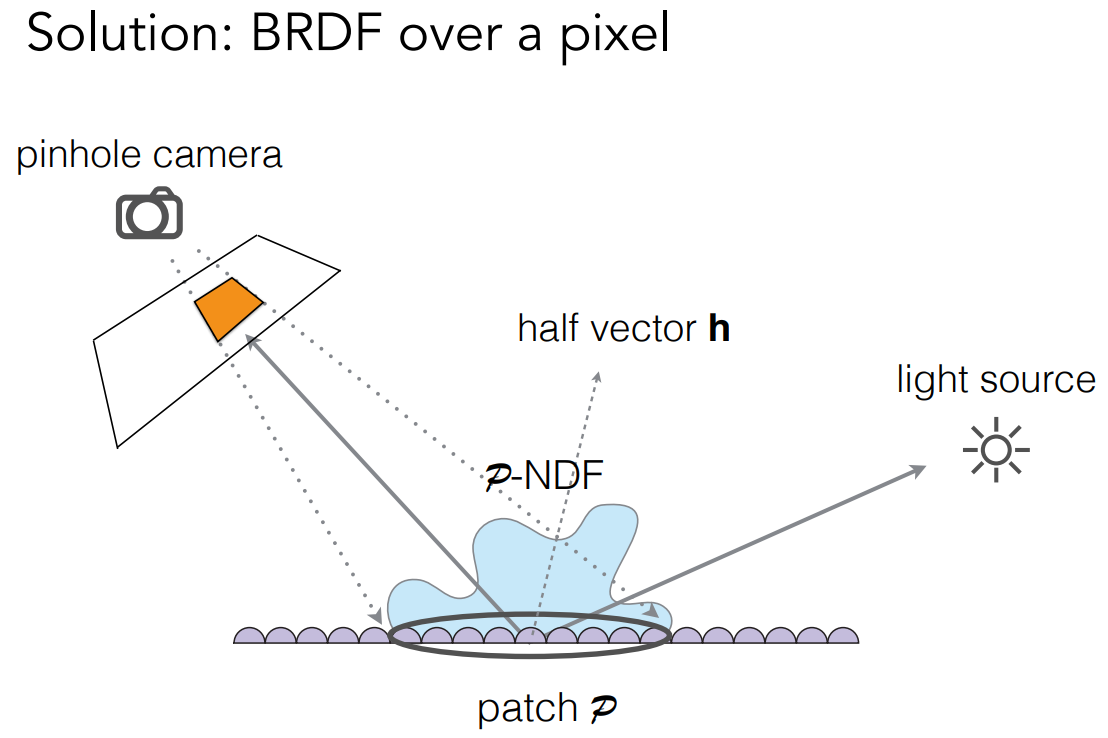
考虑覆盖的范围,会得到各种不同的法线分布(NDF)。如果像素覆盖的微表面多,就会显示出一定的统计规律;如果覆盖的少,可能会有更独特的性质
不同类型的法线贴图,也会引起不同的法线分布。刷过的平面会得到各向异性的法线分布;离散的亮片会得到很多离散的点
当物体小到一定程度(跟光波大小相似),就不能再使用几何光学进行分析了,而必须考虑对光波的衍射、干涉等现象进行模拟

波动光学的 BRDF 跟几何光学的 BRDF 相似,但多了不连续的特点。因为光会发生干涉,引起一些地方加强、一些地方减弱,形成不连续的效果
2.3 - Procedural appearance 程序化生成
程序化生成:用一定的方式指导模型 / 表面 / 材质的生成,并且不需要真正生成,可以动态进行查询。定义一个三维的纹理(可以看到物体内部长什么样子),但不需要进行存储,什么时候用到、什么时候查询。有一个空间中的函数$f(x,y,z)$,给定坐标、返回该点的纹理值。
这种函数叫做 noise function。可以对函数进行一系列处理,以得到任意不同的效果。
- 比如:设置一个阈值进行二值化,生成车子上的锈迹

噪声函数非常有用,比如生成复杂的地形、生成水面等等、生成木头的纹理等等。
再次提醒:并不是真正地生成,而是一个支持三维查询的函数。
一个专门做程序化材质的软件:houdini,在工业界被广泛地使用,它的程序化材质是真的生成。
Lecture 19 - Cameras, Lenses and Light Fields
19、20两节课是相对独立的话题,了解图形学背后的一些简单知识:相机,透镜,光场;颜色,感知
1 - 相机的曝光度(快门和光圈)
成像
成像方法:Imaging = Synthesis + Capture
- 图形学的两种成像方法:光栅化和光线追踪。这两种其实都是合成(Synthesis)的方法:物体在世界中并不存在,成像过程是合成一些不存在的东西
- 另一种方法是通过捕捉(Capture)方法来成像:真实世界中已经存在一些东西,把它们变成照片,这就是成像。一种简单的方法是用相机拍照
- 此外,也有针对其他 Imaging 方法的研究(计算摄影学),考虑其他的成像方法
相机的成像
- 小孔相机和透镜相机
- 针孔相机没有“景深”效果
- 针孔相机没有深度,每个地方拍出来都是锐利的
- 做光线追踪时也是用的针孔相机的模型
- 透镜相机带有深度,模拟其成像过程可以做出带有景深的渲染
- Shutter 快门:控制光能否进入机身,控制光在 1/n 秒内进入相机
- Sensor 传感器:把进入相机的光捕捉下来,上面的任何一个点记录 irradiance
- 不能不通过快门直接用传感器接收光,因为如果没有快门,传感器区分不出方向,传感器上的每个点都会接收来自不同方向的光(只能收集 irradiance,不能收集 radiance)
- 也有人在研究能区分方向的传感器
概念1:Field of view(FOV)视场
FOV 视场
- 视野角度大小,“广角”相机就是 FOV 大
- Focal Length(焦距)可以决定 FOV 的大小
- 定义:sensor 的高度 $h$,焦距 $f$,$\text {FOV}=2\arctan(\frac{h}{2f})$
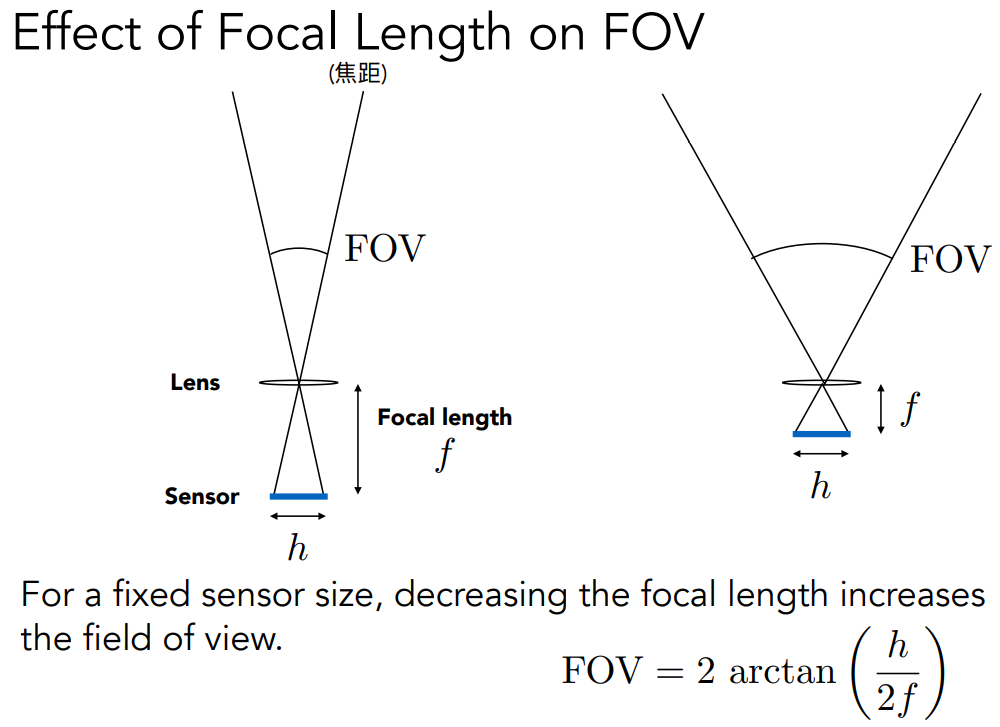
- 定义 FOV 和焦距
- 由于 FOV 跟传感器大小、焦距都有关,当定义 FOV 时,通常认为以 35mm 的胶片为传感器大小,再给出焦距的长度,以此定义 FOV 。比如单反镜头的 xx mm 说的就是焦距
- 而对于手机,给出的是等效焦距长度。手机本身很薄、胶片也更小。也就是同时缩小了 $h,f$,可以保持大的 FOV
- 同样的胶片,焦距越长,视场越小。焦距越长,看到的地方更远,视野更小
- 目前可以混淆传感器和胶片的概念。在后面的渲染中,sensor 用来记录每个像素的 irradiance,film 决定最后存储成什么样的格式
- 传感器也有不同的大小,同样能决定分辨率、视场大小
概念2:Exposure 曝光度,光圈和快门
- $H = T\times E$,Exposure = time × irradiance
- 理解:
- 在辐射度量学中,考虑的都是单位时间:单位时间光打到一个表面、单位时间光又辐射出去。irradiance 是单位时间进来多少光
- 而对于现实照相,考虑累计的时间,时间段内的所有光都进入相机、被传感器捕捉
- 对着一个明亮的场景,拍照得出的结果就亮
- 对着一个暗的场景,快门按下的时间长(曝光时间长),也可以得到亮的照片
- 对应到相机中
- T:按下快门的时间
- E(irradiance):光打到 sensor 上的一个单元的多少
- 由光圈大小 aperture、焦距 focal length 决定
- 光圈是一个仿生学的设计,仿照人的瞳孔,控制单位时间内接收光的多少。在暗处瞳孔放大,让单位时间看到更多光
- 理解:
- 曝光度可以度量为照片亮的程度。相机中影响成片亮不亮的因素:
- Aperture size:光圈的大小,f-stop 参数可以控制光圈的大小
- Shutter speed:快门开放的时间
- ISO gain(ISO增益,感光度):一个后处理,给感光的结果乘上一个数
- 观察图中的参数变化对应照片变化
- f-stop 越大,光圈越小,图像越锐利。光圈越大,在一定范围内图像更虚
- shutter speed 开放时间越长,捕捉到的运动信息越多
- ISO 乘上的数越大,在放大信号的同时也放大了噪声
- 再看快门和光圈
- 光圈的 f-number(f-stop)就是 Exposure Levels
- 调节光圈就调节了固定时间内进入相机的能量,也就是直接调节了曝光度
- 非正式的理解:f 数是光圈的直径的倒数
- 机械快门有一个快门打开的过程
- 如果过程中物体产生了运动,就发生运动模糊。时间段内所有的信息都被传感器记录下来并取平均。这也是手抖拍照模糊的原因
- 减小快门时间,运动模糊的程度就降低了,但为了维持亮度,要调大光圈或用大 ISO
- 运动模糊也不一定是坏事!
- 在人的感知方面,运动模糊可以体现物体的动态感
- 以采样的角度考虑:对于光栅化的采样,如果采样率不够、即两个像素之间距离远,就会产生走样(锯齿),需要进行反走样,即先模糊、再采样。而运动模糊相当于在对时间的采样中做了反走样
- 快门打开的过程同样造成 Rolling shutter 问题,光进入相机的时间不一样,导致照片中不同位置记录的是不同时间进入的光。视觉上,极高速运动中的物体会产生扭曲的效果
- 如果过程中物体产生了运动,就发生运动模糊。时间段内所有的信息都被传感器记录下来并取平均。这也是手抖拍照模糊的原因
- 需要进行光圈和快门的权衡
- 如 f-stop 从4到8,对应光圈面积变为1/4,那么需要快门时间变成4倍
- 对于高速摄影,要求快门时间小,那么光圈面积就要调大(f-stop 调小)
- 对于延时摄影,用小面积的光圈长时间曝光
- 在摄像时,不能兼顾景深和运动模糊两个效果

- 光圈的 f-number(f-stop)就是 Exposure Levels
2 - 相机的镜头(透镜)
Thin Lens Approximation
真正相机的镜头是很多复杂透镜的组合,我们研究理想的薄透镜作为近似。
- 平行的光线经过透镜后汇聚到一点,称为 Focal Point 焦点,透镜到焦点的水平距离称为焦距。
- 光线是可逆的,过焦点的光通过透镜后变成平行光
- 任意一条光线,如果过透镜的中心,它的方向不会发生改变
- 假设薄透镜的焦距可以动态任意更改(模拟现实相机的透镜组)
薄透镜方程
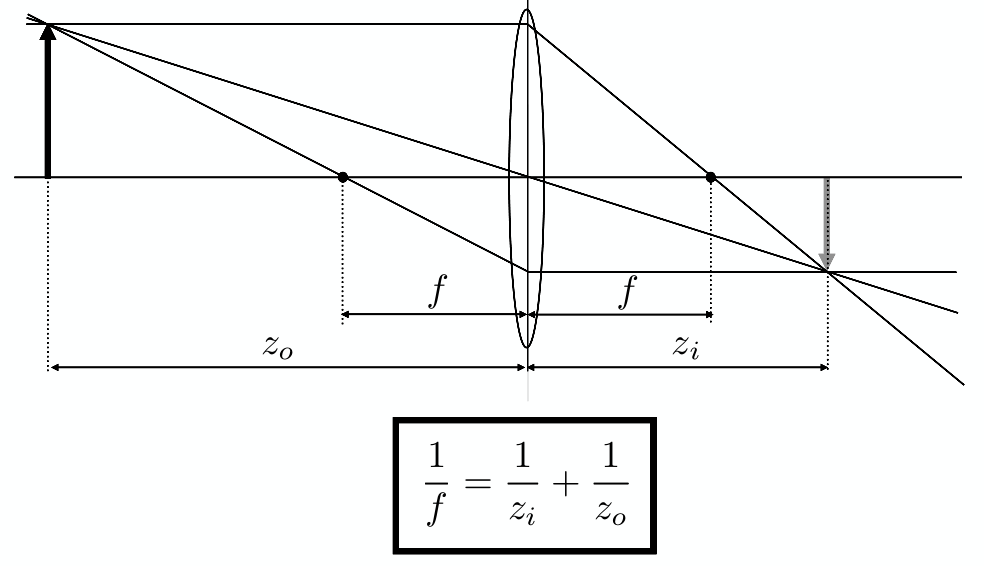
- 物距 $z_0$:物体到透镜的垂直距离,相距 $z_i$ :成像到透镜的垂直距离,焦距 $f$
- $\frac{1}{f} = \frac{1}{z_i} + \frac{1}{z_0}$,展示了焦距、物距、相距的关系
- 计算方法:根据两条性质①过焦点的光线经过透镜变平行,②平行光线经过透镜过焦点,构造两组相似三角形
- 由这个方程,物体的物距改变了,相距也要随之改变
通过薄透镜,就可以解释很多的问题。
Defocus Blur
Circle of Confusion(CoC)
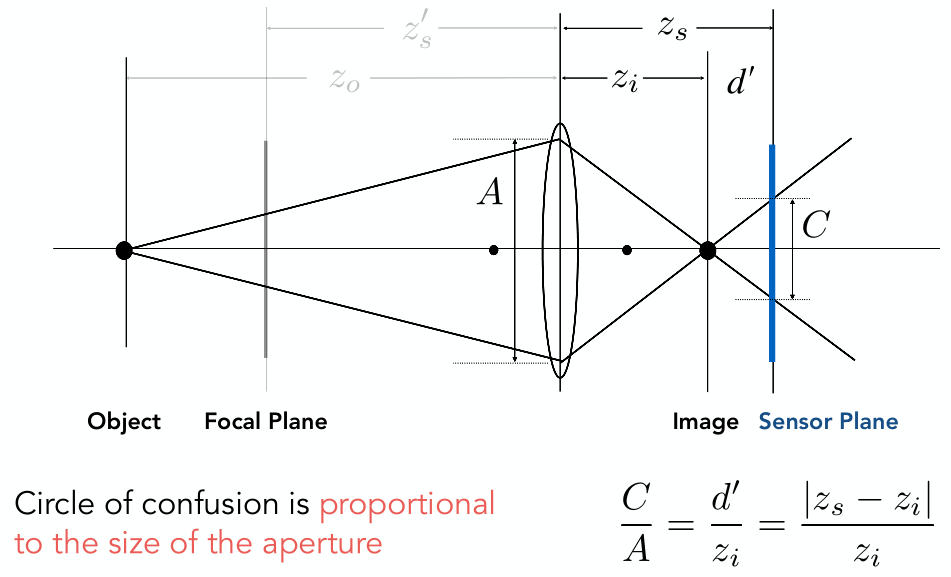
- 如图,在 Focal Plane 平面上的点,经过透镜聚焦在 Sensor Plane 上(看 $z_s’$ 和 $z_s$)
- 而如果物体不在 Focal Plane 平面上,而在 Object 处的一个点,经过透镜聚焦在 Image 上($z_0$ 和 $z_i$) ,光线继续传播到 sensor 就会变成一个圆
- 在这个圆内,分不出来是从哪里传来的光线,称为 Circle of Confusion
- 构造相似三角形也能求得 CoC 的公式,如上图。发现 CoC 的长度 $C$ 跟透镜的长度 $A$ 呈正比

- 看到的东西是否模糊取决于光圈的大小,光圈越大越模糊
- 光圈为 f/1.4 (大光圈),看到的效果更模糊;f/22 的小光圈的图片更清晰
- 这也是在第一节中展示的光圈大带来景深效果的原理
- CoC是景深、近视等现象的成因
在此,重新更加准确地定义 f-stop:
- f 数是焦距除以光圈的直径,$N=f/A$
- f 数通常写作 f/2,反应绝对光圈直径 (A) 可以通过将焦距 (f) 除以相对光圈 (N,f数) 来计算
因此:
- COC除了跟透镜大小(光圈大小) $A$ 呈正比,也理解为跟 f 数 $N$ 呈反比,总之要拍摄清晰的图片就选择小光圈
Ray Tracing Ideal Thin Lenses
之前的 path tracing 产生光线的方法是:从相机往每个像素的采样点发出光线,这是小孔成像的模型。
现在,已知了光线穿过薄透镜的行为,因此可以用薄透镜来计算光线追踪的过程、渲染成像。
- 定义 sensor,即成像平面的大小;定义透镜的属性,即焦距和大小
- 对于某个想要成像的物体(平面),定义透镜摆放的位置(物距 $z_0$)
- 由透镜公式,已知物距、焦距,计算相距 $z_i$
- Ray Tracing 的过程:
- 希望找一些光线能够穿过透镜打到场景中
- 由于对于 sensor 的每个点 $x’$,穿过透镜中心点光线一定打到 $x’’’$ 处
- 在透镜选一个点 $x’’$,就知道从 $x’$ 穿过 $x’’$ 打到 $x’’’$ 的方向
- 只需考虑 $x’’\rightarrow x’’’$ 这条光线上的 radiance,计算出来后记录到 $x’$
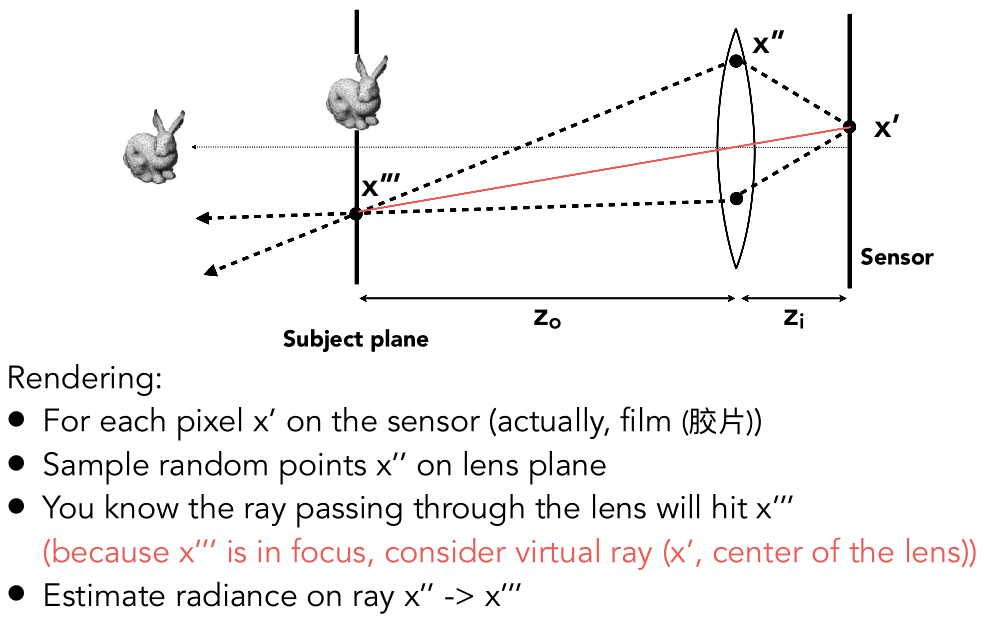
Depth of Field
用 Defocus blur 正式定义景深的概念:
- 用大光圈,CoC 的面积就大,图片更加模糊;但在刚好对焦的平面附近不会出现 CoC 现象,不会模糊。大、小光圈会影响产生模糊的(深度)范围
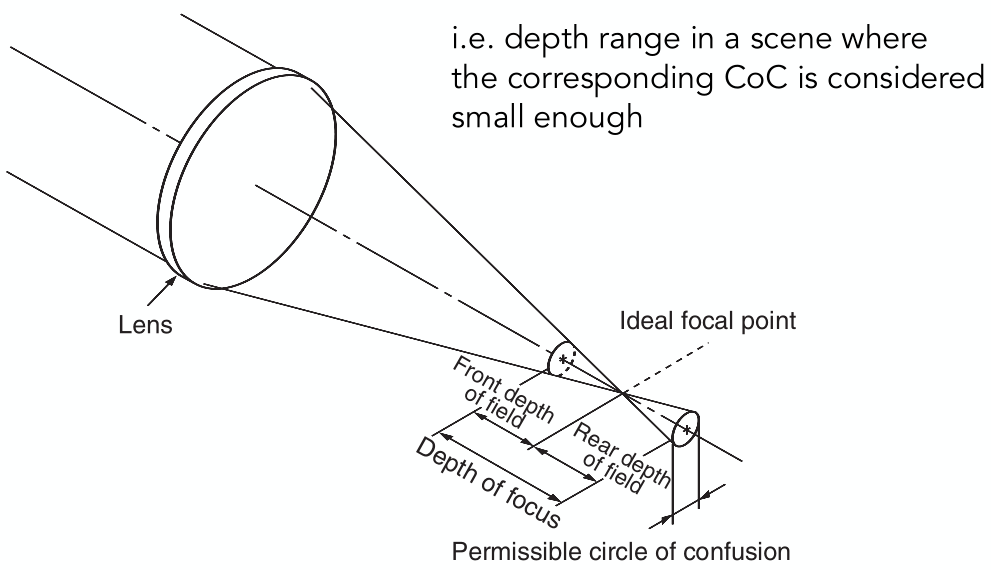
- 在对焦附近的区域,CoC 足够小,看上去是清晰的,就是景深
- 光经过透镜,打到成像平面上。在成像平面附近的一段区域内,都认为 CoC 是足够小的
- 景深:在实际场景中有一段深度,经过投影后会在成像平面附近形成一段区域,这段区域内 CoC 足够小。计算景深就是在成像平面附近范围内,对应到场景中的深度范围
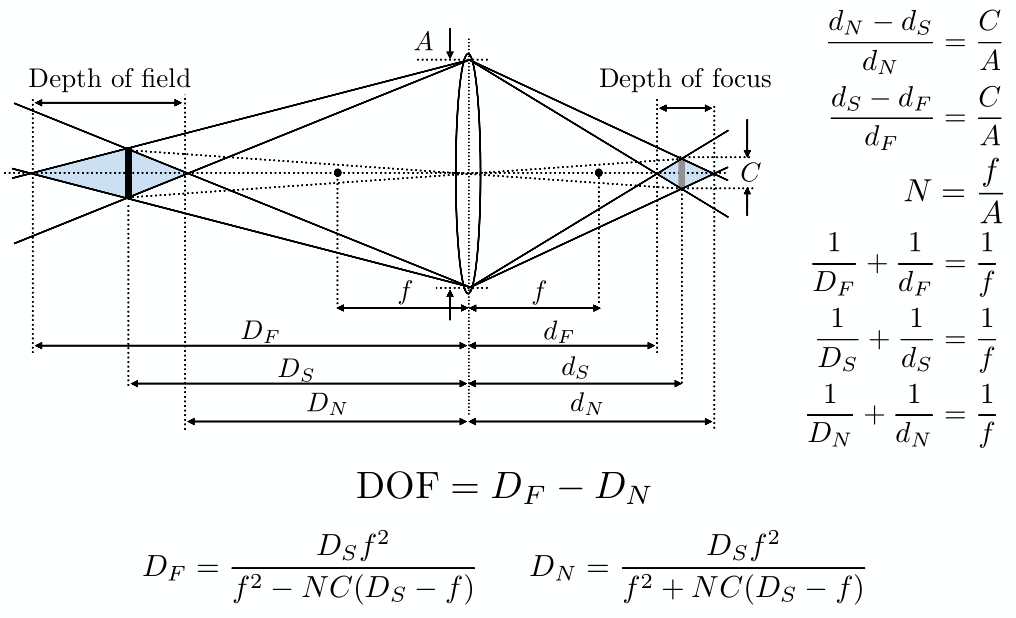
- 可以在网站上尝试:Depth of field (stanford.edu)
3 - Light Field / Lumigraph 光场
全光函数
定义人如何看到世界:全光函数
- 对于人来说,看到的都是来自各方向的光,而不在意深度信息。因此,可以用一个 2D 的屏幕记录来自各方向的光,如果人看向这个屏幕,会感到自己在看向 3D 的场景。这就是虚拟现实的原理。
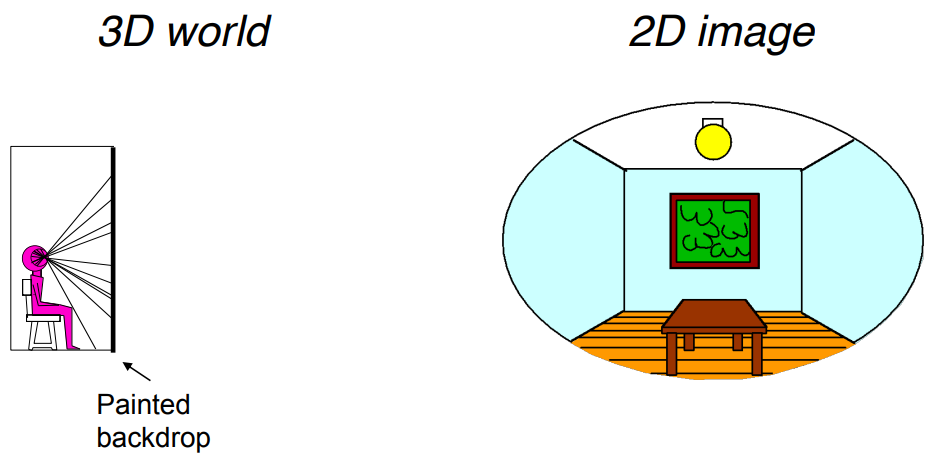
可以用一个函数来描述人眼所能看到的所有东西:全光函数(The Plenoptic Function)
假设一个人站在一个场景里,往任何方向去看。
- 用极坐标定义一个方向 $\theta,\phi$ ,定义在这个方向看到的值为 $P(\theta, \phi)$
- 引入波长(各种颜色)的概念 $\lambda$,可以看到彩色的世界 $P(\theta, \phi,\lambda)$
- 扩展到时间,成为电影 $P(\theta, \phi,\lambda,t)$
- 如果人的位置可以在三维空间中移动,看到的是全息电影 $P(\theta, \phi,\lambda,t,V_X,V_Y,V_Z)$
- 最后,不把函数当作电影,而是理解成:在任何位置、任何时间,往任何方向看,看到不同的颜色,这就是我们能看到的所有东西——整个世界就衡量为一个 7D 的函数,称为全光函数

从全光函数定义光场
光场是全光函数的一部分
- 光线 Ray
- 5D 的定义
- 3D 表示空间中一点,2D 表示极坐标一个方向
- $P(\theta, \phi, V_X,V_Y,V_Z)$

- 4D 的定义
- 两个点定义一条光线,2D 位置 + 2D 方向
- 为什么是 2D 位置在接下来的光场定义中给出
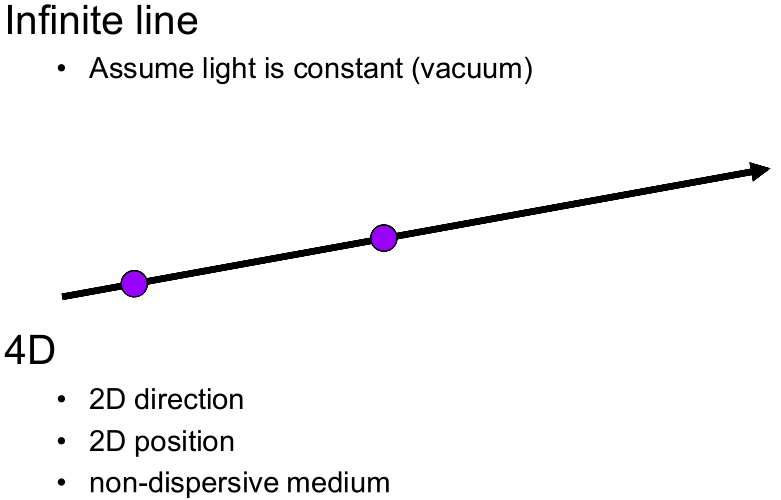
- 5D 的定义
光场是什么
- 当看向一个物体时
- 对于一个物体,会从任意位置、任意方向看向它
- 由于光线是可逆的。也就可以反过来,描述物体能被看到的所有情况:描述物体在包围盒上的任何位置,往任何方向的发光情况
- 由此,当看向物体时,可以从对应包围盒上点的对应方向进行查询。
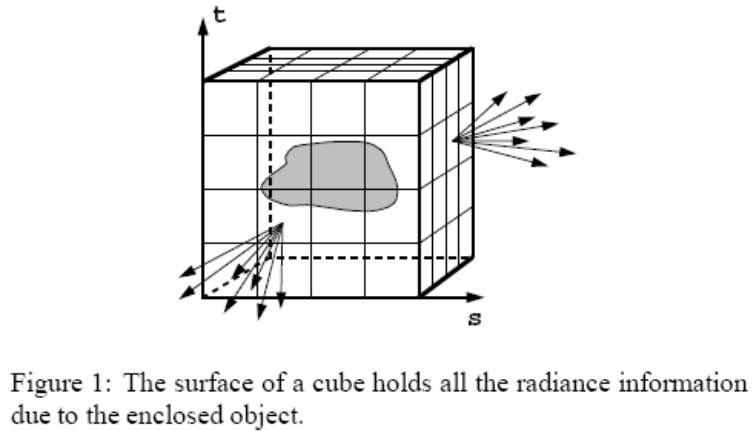
- 这个记录发光情况的结构就是光场
- 光场:在任意位置,往任意方向发出光的强度。2D 的位置,2D 的方向。
- 位置:3D 物体的表面是在 2D 空间中的(如 UV 纹理映射,这里的包围盒也是一个贴图)
- 方向:空间中的方向用 $\theta,\phi$ 表示
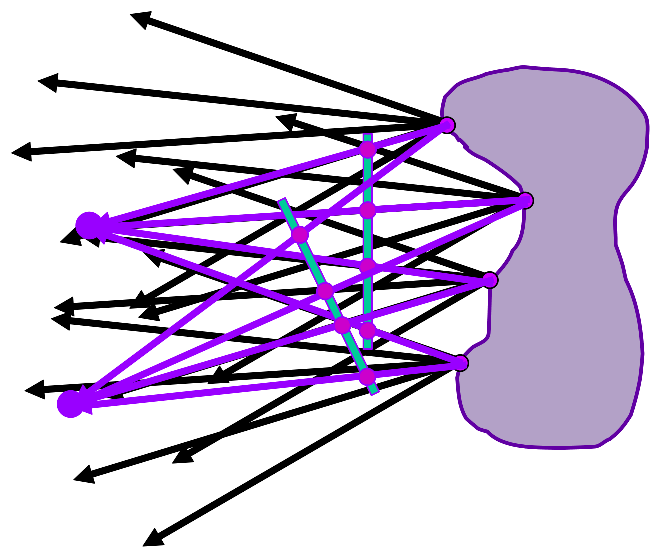
- 如图紫色连线,在任何一个位置放置摄像机,通过查询光场,都能得出:看向物体的任意一个点,看到的光的情况
- 光场的好处就是:可以得出任意一个方向的观测结果
光场概念的一些理解
- 正如人眼不关心看到的是 3D 空间还是 2D 屏幕,光场可以定义在物体表面,也可以定义在物体外的一个黑盒上,只要定义黑盒表面任意一个位置的光线情况,就可以记录它的光场
- 推广这个理解,取一个平面,右边是一些发光物体、发出光穿过平面。对于光场只需要知道平面左边的情况,而对右边的物体不关心
- 知道平面上的任意一点 $S$、知道一个方向 $\theta,\phi$ 即可定义任何一条光线
- 知道平面上的任意一点 $S$、知道一个方向 $\theta,\phi$ 即可定义任何一条光线
- 进而,对于任何一个光场,都可以用两个平面来定义
- 分别取两个平面上的一个点,就能定义任何一条光线
- 对光场进行参数化:
- $u,v$、$s,t$ 表示两个点,找到所有两个点的组合、记录光线的情况,就是光场的参数化方法
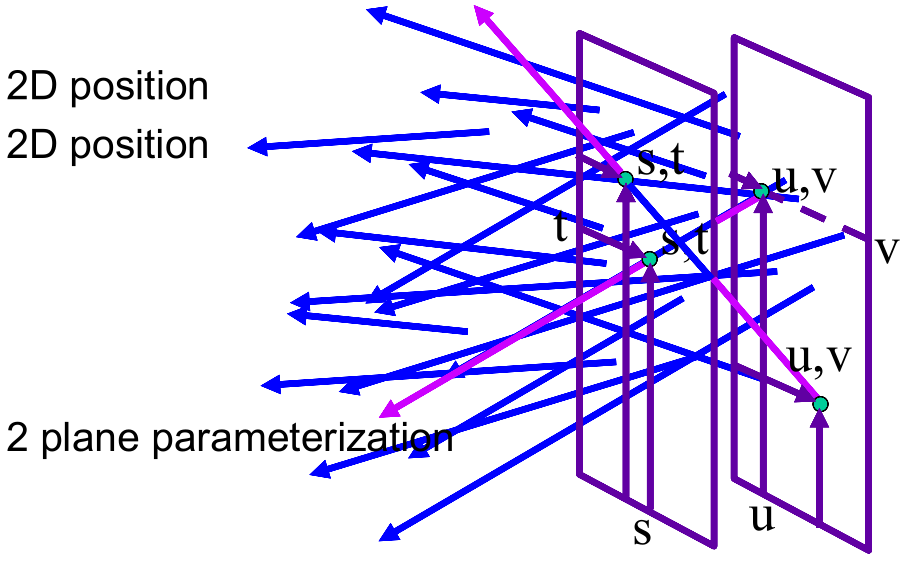
- 分别取两个平面上的一个点,就能定义任何一条光线
对于“两个平面”光场参数化方式的不同理解
两种理解方式
按照如图方式放置两个平面,整个世界在 $s,t$ 平面的右边
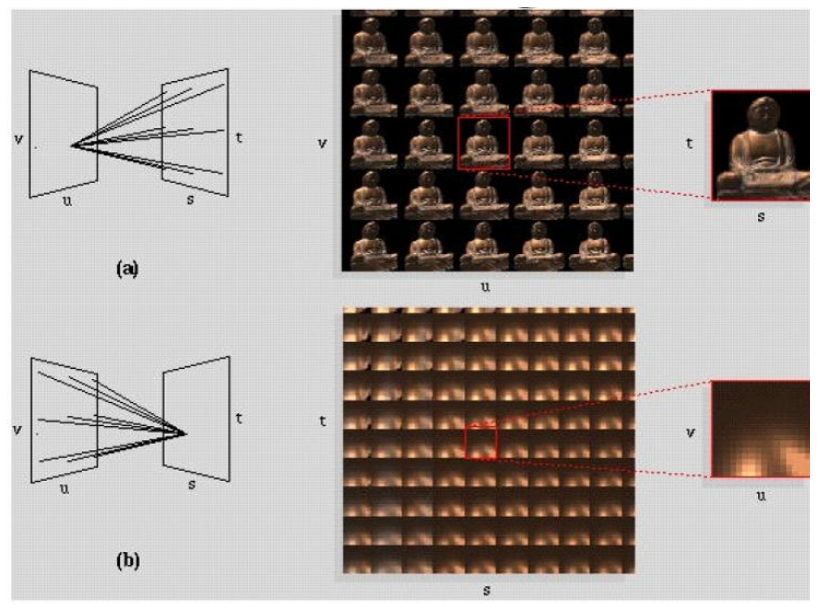
理解一
- 固定在 $u,v$ 上取一个点,看向 $s,t$ 平面上所有的点,会看到一个完整的物体图像
- 整个 $s,t$ 平面就是完整的物体
- 因为 $s,t$ 平面右边就是世界(不关心它具体是什么),相当于小孔成像
- “摄像机阵列”:有很多摄像机,分别从某个角度看向世界、拍一张图,组合起来成为光场
理解二
- 固定在 $s,t$ 上取一个点,看向 $u,v$ 平面上所有的点
- 反过来考虑,从 $u,v$ 平面上任何一个点都看向 $s,t$ 上的同一个点,可以看到一个物体不同方向的一个像素
- 光场中, $s,t$ 上的一个点就是物体的一个像素。从不同的方向看向这个像素
- 可以理解为:物体一个点上的 irradiance,通过这种方式拆成了 radiance。可以看到物体的任意一个像素,打到不同方向上的光到底是什么
- 自然界中一些生物的复眼成像原理就是在呈现一个光场
- 平时拍出的照片,每个像素记录的是 irradiance:不区分光来自的方向,而进行平均
- 如果用小的透镜,把来自各个方向的光分到不同位置上,就可以把原本打到一个像素上的光分到不同的 sensor 上记录,如图把红、绿、蓝光分别进行记录;看向一个像素时,其实是看向穿过像素的、不同方向的光
- 本质上,这就是记录了 radiance 而非 irradiance,这就是光场摄像机的基本原理:使用一个透镜,把来自不同方向的光分开,分别记录下来
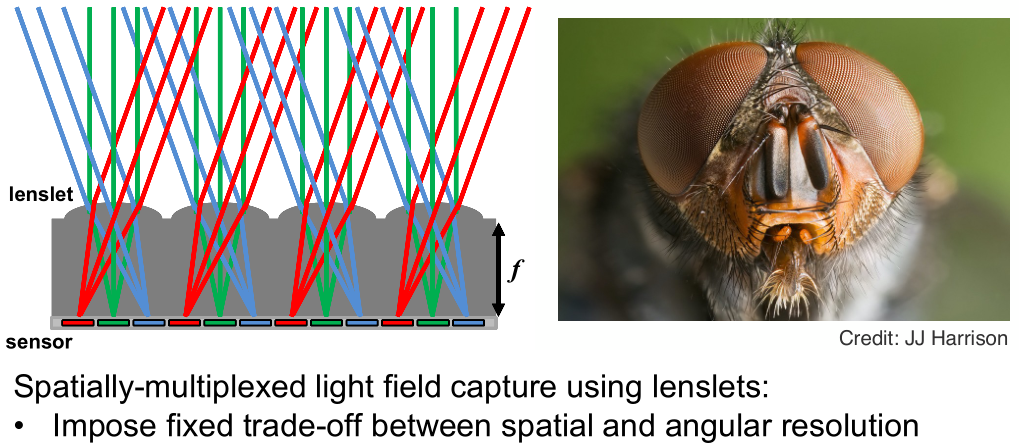
4 - Light Field Camera 光场摄像机
光场摄像机:
- 一个功能:可以先拍照,然后后期动态地调整焦距、光圈大小等
- 原理:把像素换成一个微透镜,把来自不同方向的光分开,再在后方的sensor上分别记录下来(把感光元件往后挪)
- 原本的一个像素,变成在光场照相机内记录一块像素,也就是 irradiance 被拆分成了 radiance
- 如果还原成一个普通的照片,就在每一个透镜都选择一条光线、记录在对应每个像素的结果上,就得到一张原始的照片。这就相当于把摄像机放到某个方向来拍摄
- 有了光场,就可以虚拟地移动拍摄的位置了。光场摄像机可以移动摄像机的位置
- 重新聚焦也是相似的道理:由于拥有整个光场,可以按需查找需要改变的光线,计算应该取哪些方向
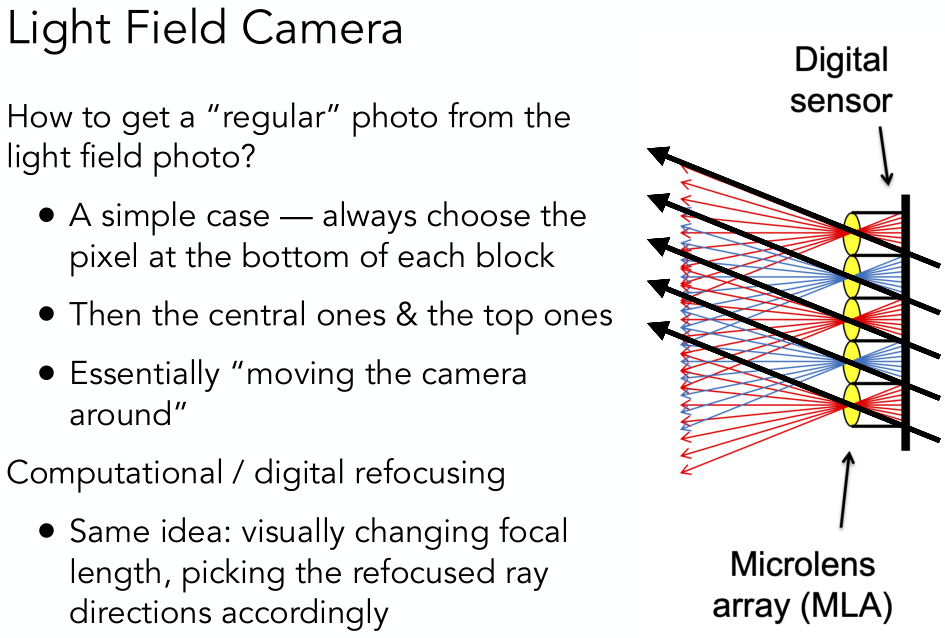
- 总结起来,光场摄像机的种种功能,来自于其记录了光线的所有信息,包括位置、方向
- 此外,光场摄像机的一些不足:
- 对胶片分辨率要求高:原本一个像素的信息,现在需要用更多的像素来记录(原来的位置分辨率×方向分辨率)
- 高成本:分辨率问题,微透镜的实现问题
- trade-off:更精密的方向信息 or 位置信息

Lecture 20 - Color and Perception
- what is color
- color perception
- color reproduction / matching
- color space
1 - What is color
Physical Basis of Color
Spectrum 光谱
- 颜色是一个混合出来的结果:用棱镜可以把光线折射、分解成不同的颜色,将它们混合起来又形成原来的光线
- 原因是不同的波长对应不同的折射率,而任何一种光都对应一种光谱,光谱就是光线的能量在不同波长上的分布
- 图形学关注可见光的光谱范围:400-700nm。
Spectral Power Distribution (SPD) 谱功率密度
- SPD 衡量了光线在不同的波长的强度是多少
- 通过 SPD,可以描述各种光在各个波长上的分布,不同的光对应不同的SPD
- 对于蓝天,集中在小波长、高频区域,看上去是蓝色;对于阳光看上去又是另外的样子

- SPD 具有线性性质:用不同的光照射同一个物体,分开的 SPD 加起来就是共同照射时的 SPD。理解为两个灯一起开会更亮
从光谱到颜色:颜色是人的感知,而不是物理上的概念
2 - Color Perception
Biological Basis of Color
人的眼睛就是一个摄像机
- 对应各个部位
- 瞳孔:光圈;晶状体:透镜;视网膜:sensor
- 在视网膜上,有感光细胞
- 棒状细胞感知光的强度,用它得到一个灰度图
- 锥形细胞比较少,可以感知颜色
- 锥形细胞内部又分为三种不同的锥形细胞:S、M、L 型细胞,分别更擅长感知高、中、低波长对应的光
- 每个人体内三种锥形细胞的分布也大不相同,每个人对颜色的感知不一样
Tristimulus Theory of Color
目前,知道了不同的光在波长上的分布 SPD,又知道了每一种细胞对于不同波长的响应方式,就可以计算感知的结果了。用响应曲线跟 SPD 做波长上的积分即可。
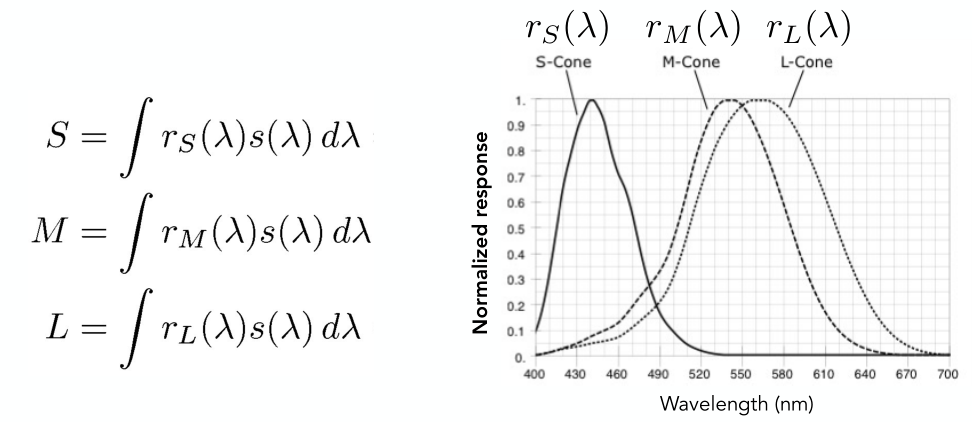
- 对于不同的SPD,人们看到了三个数:S、M、L
人们看不到光线、光谱,只看到积分出来的结果也就是三个数
Metamerism 同色异谱
由于人只看到结果,会不会出现:两个光线、光谱不相同,但积分的结果相同,看上去是一样的?这种现象就叫做同色异谱现象。
正是应用了这种现象,才能给人们呈现各种各样的颜色。
- 假如拍了一张照片,并希望能在电视上显示出来,就进行光谱的调节,使得在电视上和自然界中,人看上去是一样的颜色
- 通过调和光谱,得到某一种颜色,使得这种颜色跟另外一种颜色看上去一样,这叫做 color matching 颜色匹配过程。不需要光谱一样,只需要最后看到的颜色一样
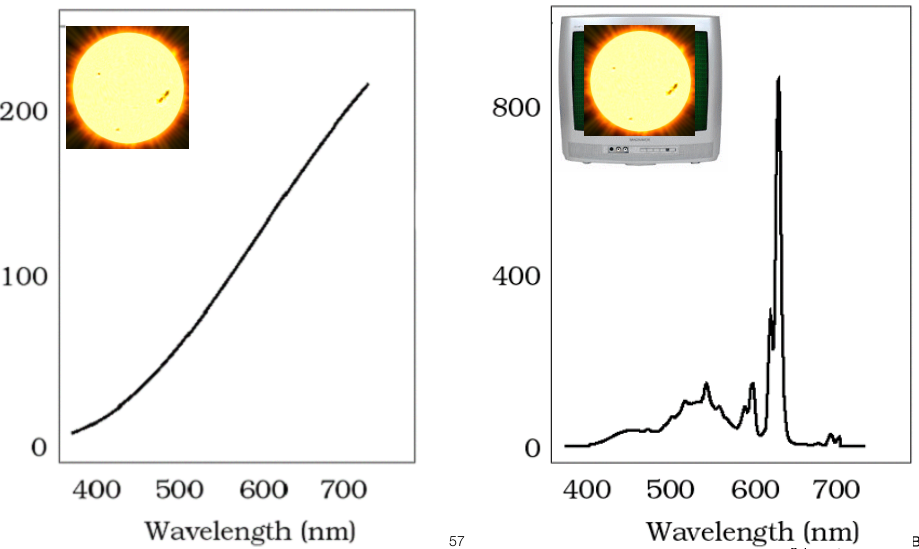
- 接下来就是如何进行 color matching
3 - Color Reproduction / Matching
Additive Color 加色系统
颜色的混合
- 有几种不同的颜色,以 RGB 为例,各自有不同的 SPD
- 把 RBG 各自乘上某个强度,然后混合(相加)
- 最终得到一种颜色,用各自混合的强度系数来表示这个颜色

计算机中的加色系统
- 在计算机中,把 R、G、B 的强度都调成255,会得到白色。真实世界中也是如此
- 画画中,调和不同的颜料会越调越黑,是减色系统
- 加色系统可以实现:通过基本颜色的线性组合,匹配各种不同的颜色
- 也有的颜色不能匹配出来(因为任何一个基本颜色的强度都不能减到0以下),这时由线性性质,给待匹配的颜色加上某个值,相当于在匹配中减去某个值,依然是一个线性的组合
CIE RGB 系统
- 给定3种 SPD 是单波长的颜色,作为基本颜色,给定单波长需要混合的颜色。考虑如何用这三种单波长颜色,混合出某一个波长上对应的颜色
- 对每一个给定波长进行试验,得出每个波长上对应的三种单波长基本颜色的线性组合系数,绘制匹配函数图像
- 这样,知道了每个单波长的颜色混合方式
- 对于真实情况的多波长分布 SPD:
- 给定任何一个实际的 SPD,只需分别对于每个单波长,考虑要用多少的 RGB 即可
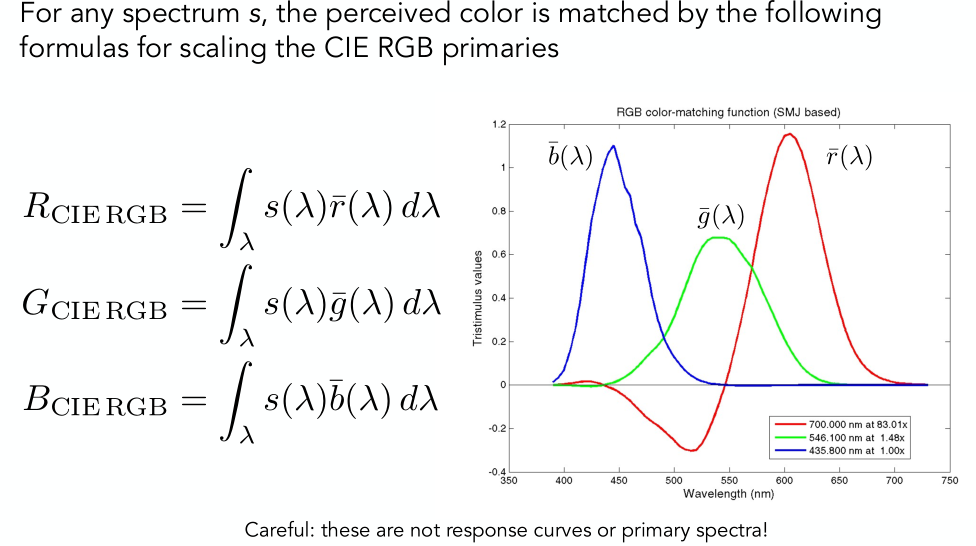
- 也就是,先用单波长混合出任意的单波长颜色,然后在波长上积分,求得任意多波长 SPD 的总的 RGB 混合方式
4 - Color Space
XYZ 颜色空间,色域
已经有了广泛使用的 sRGB(Standardized RGB) 系统
- 先找一台机器做好它的RGB,后面的机器就按照这个方法来制造
- sRGB 广泛应用于各种成像设备
- RGB 系统所能形成的 gamut(色域)是有限的
另外一个系统:CIE XYZ
- 不是像 RGB 系统一样,用实验测出来颜色的匹配,而是人造的颜色匹配系统,事先定义颜色匹配的曲线
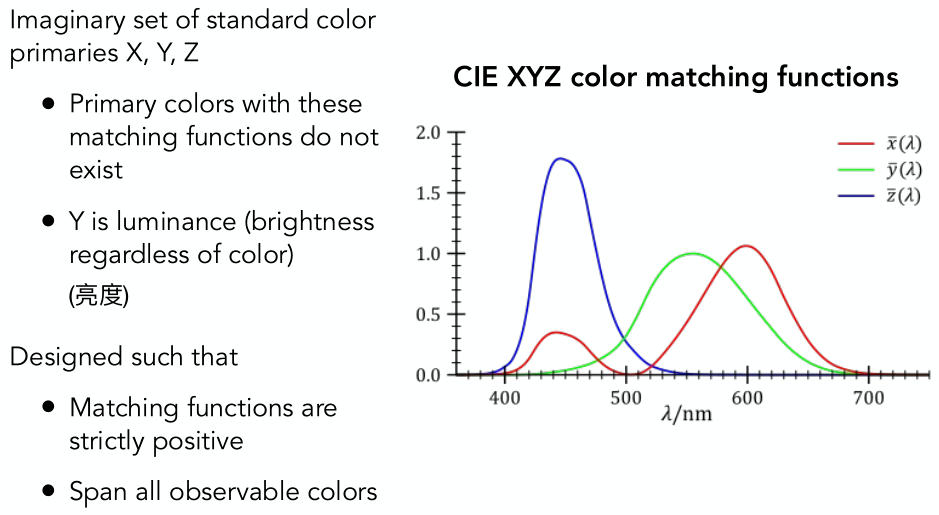
- 具体设计
- X 有两个峰值、没有负数,整个波长空间上都有分布
- Y 分布比较正常,表示亮度 luminance
- 可视化
- 先做归一化到 $x,y,z$ ,只需显示两个维度就可以在 2D 平面上可视化了
- Y 表示的是亮度,可以把亮度固定,然后让 X、Z 变化,画图画 $x,y$
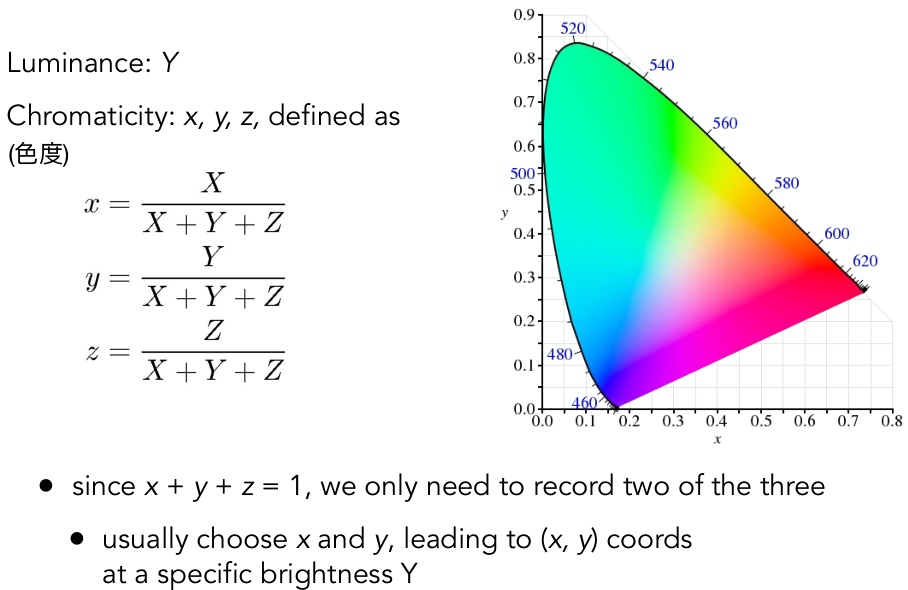
- 看到的是一个颜色空间能显示的所有颜色,称为 gamut 色域
色域
CIE XYZ 的色域
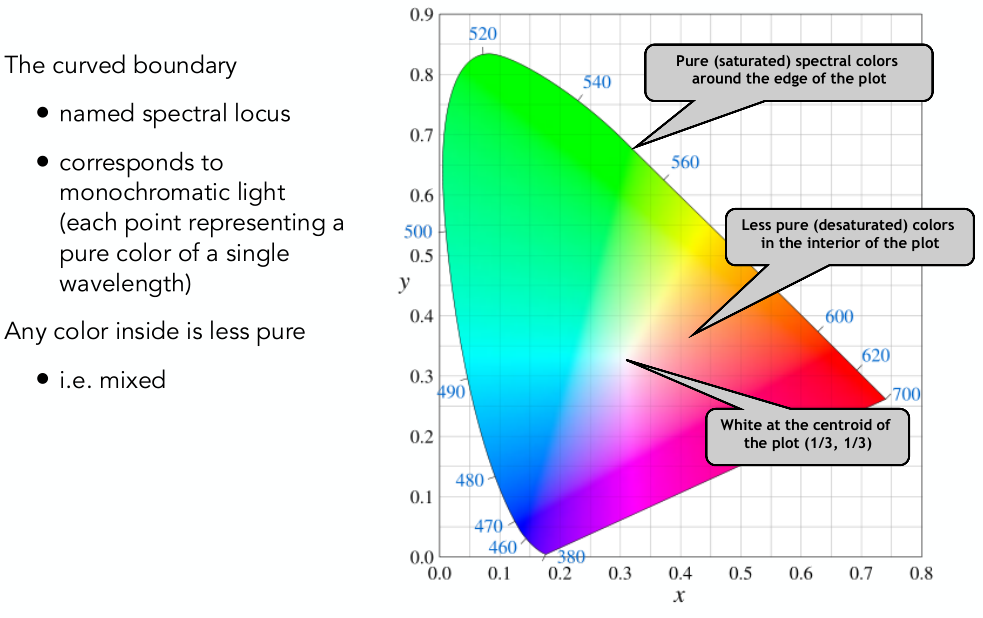
- 中间是白色,是混合而成的、最不纯的颜色。纯的颜色在边界
RGB 的色域
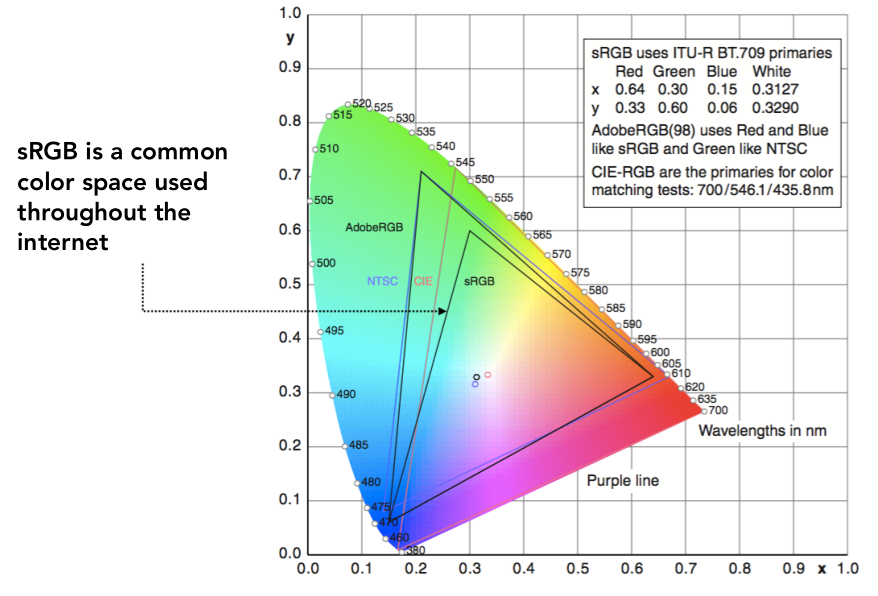
- 可以看到,RGB 的色域是 XYZ 色域的子集。对于 sRGB,色域只是一个三角形,表示不了 CIE XYZ 这么大的色域
其他的颜色空间,Perceptually Organized Color Spaces
HSV颜色空间
- 组成
- Hue(色调):不同类型的颜色
- Saturation(饱和度):更接近白色,还是更接近纯色
- Brightness / Lightness / Value(亮度)

- 类似的基于感知的颜色空间(Perceptually Organized),比 RGB 等更方便艺术家们选择颜色,在颜色拾取器中被广泛使用
CIELAB Space (aka L*a*b*)
- 组成
- L*:亮度
- a*、b*:两端表示互补色

Misc.
由于颜色是感知,有一些奇妙的现象
- 互补色:人脑的视觉暂留现象就是在长时间看一个图片后,切换后会看到它的互补色。具体的互补色组合经过实验确定
- 一切都是相对而言
- A 和 B 的亮度相同
- 两个 X 的颜色相同
- A 和 B 的亮度相同
典型的减色系统:CMYK
- 减色系统在打印中常用
- 在减色系统中,把不同的颜色混到一起会越混越黑
C:品蓝,M:品红,Y:黄色,K:黑色
CMY 就可以混合出各种颜色
加一个 K 是因为打印常用黑色,如果混合来用会增加很多成本

本课程未提及的部分:
- HDR(High Dynamic Range),当颜色亮过了白色,会不会还能更亮
- 伽马校正:之前提过,在 path tracing 最后算出了 pixel 的 radiance,radiance 最后要变成颜色,做简单的线性变换是得不到的。颜色在显示器上是非线性的,必须先校正过来,使得两部分非线性抵消后还是线性
Lecture 21 - Animation / Simulation
这节课:概念,下节课:解法
Introduction to Computer Animation
- History
- Keyframe animation
- Physical simulation
- Kinematics
- Rigging
1 - 计算机动画
动画是什么
- 刚开始,动画是“Bring things to life”,更多作为交流的工具,更关注美学
- 在图形学里,也可以把动画理解成:对于建模和几何的一种拓展,把3D模型延伸到时间的维度上
- 动画的形成:由于人眼的视觉暂留效应,把很多图片按顺序、按一定速度播放即可
- 不同的应用对动画的帧数要求不同:电影 24fps,视频 30fps,游戏 60~144fps,VR 90fps
一些里程碑
- 1878年出现了电影
- 1937年,迪士尼制作了第一步手绘、剧场版长度(40min)的动画《白雪公主和七个小矮人》
- 1963年,首个遥控笔控制、电脑生成的图形动画,由 Ivan Sutherland 演示
- 1972年,Ed Catmull & Frederick Parke 的计算机动画人脸
- 1993年,电影《侏罗纪公园》把恐龙的模型做进电影里
- 1995年,第一步完全由电脑生成的动画电影《玩具总动员》(光栅化)
- 之后,动画电影进一步发展(光线追踪)
- 到2019年,《冰雪奇缘2》植物、头发的细致渲染
2 - 关键帧动画
- 关键帧定义整个动画的走向
- 中间补充过渡帧,可以自动生成
- 本质上是一种插值技术,在不同关键帧对应的点之间进行插值
- 可以用曲线、样条来控制插值的方式,在需要的地方分别应用线性插值或其他插值方法,这就是动画跟之前的几何有关联的地方
3 - 物理模拟动画
物理模拟基本
- 除了插值,更多情况下使用物理模拟的方式来制作动画
- 把牛顿第二定律 $F=ma$ 应用到物体的质点,物体本身有一个质量、对其施加一个力,物体就会获得一个加速度
- 有了加速度,就能计算速度;有了速度就能计算位置。也就是知道了物体的力和初始条件,就能动态地更新物体下一个时刻的位置
- 对于简单或复杂的物体,只要能够建立正确的物理模型,包括进行正确的受力分析,并且物体本身的建模足够好,就能通过解一些数值方程来正确模拟各种动画
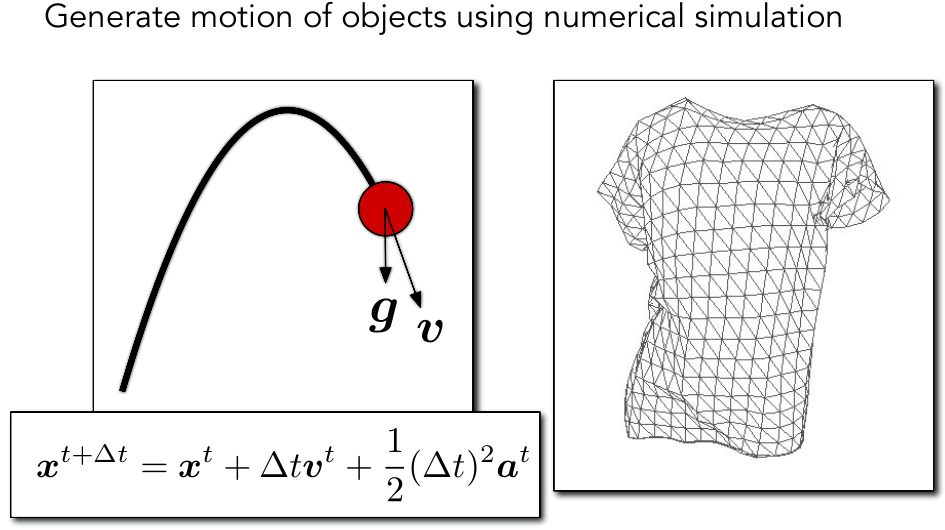
- 一些例子
- 布料模拟 Cloth Simulation:衣服跟着人的运动而运动,涉及到各种摩擦力、压力的计算;为了衣服不会穿模,需要进行各种碰撞检测
- 流体模拟 Fluids:首先模拟各处水滴的形成,位置、形状、运动状况;然后进行渲染、得到外观上的样子
Mass Spring System 质点弹簧系统
需要建立物体之间的相互作用模型,模拟物理效果,来正确模拟物体的运动。质点弹簧系统是一个简单并且实用的系统。
质点弹簧系统的一些应用:HW8 绳子模拟;头发被风吹起的效果(考虑本身重力、之间的摩擦力、风力等);布料动态效果的模拟等。
基本单元
质点弹簧系统是一系列相互连接的质点和弹簧,基础单元是一个弹簧左右连接着两个质点
- 弹力
- 理想的弹簧:没有长度,被拉开多长就产生相应多大的力(由胡克定律确定)
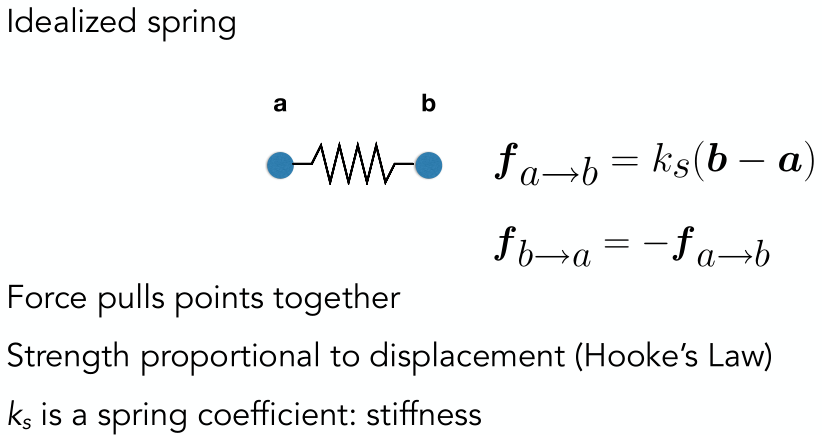
- $f_{a\rightarrow b}$ 表示 $a$ 点被拉向 $b$ 点的力
- 它的问题:现实的弹簧不会没有长度
- 对于一般弹簧,本身有长度,考虑拉伸它的情况
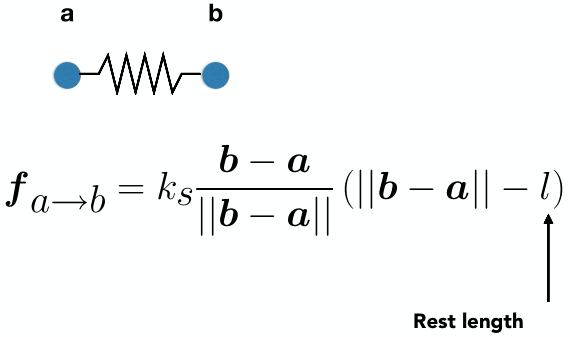
- $(||b-a||-l)$ 是拉开的长度,$\frac{b-a}{||b-a||}$ 是受力的方向
- 它的问题:会永远震动下去
- 理想的弹簧:没有长度,被拉开多长就产生相应多大的力(由胡克定律确定)
- 摩擦力
- 需要添加摩擦力(damping),让弹簧能够停止
- 先介绍一个记号:在仿真中,用 $x$ 表示(位置),那么用 $\dot x$ 表示一阶导数(速度),用 $\ddot x$ 表示二阶导数(加速度)
- 给弹簧施加一个跟速度相反的力 $f=-k_d\dot b$ ,来让弹簧停下来
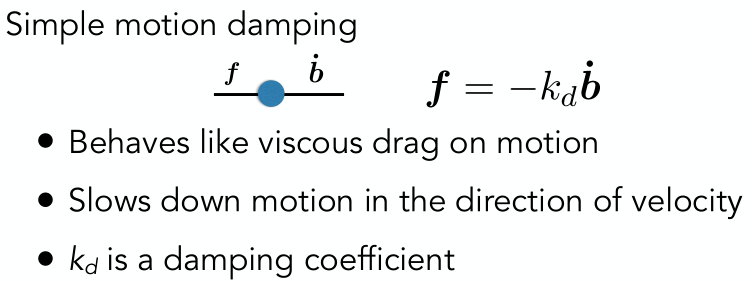
- 它的问题:会引起所有的运动都停下来
- 弹簧向一个方向平移运动,即使不进行拉伸(内部没有力),也会因为有速度而停下来
- 只能描述弹簧外部的力,无法描述弹簧内部的力
- 用相对运动关系描述弹簧内部的力

- $\dot b-\dot a$ 是相对速度,$\frac{b-a}{||b-a||}$ 是受力的方向(单位向量,沿着ab方向),$\frac{b-a}{||b-a||} \cdot (\dot b-\dot a)$ 就是相对速度在受力方向上做投影的长度,即相对速度在受力方向上的速度是多少(算出来的是一个数,是标量)
- 有一些速度不影响弹簧的长度,比如 b 围绕 a 做圆周运动。这一步投影就是排除 ab 方向以外的速度,相对速度为 0 就没有摩擦力
- 然后用这个数做跟之前一样的计算,乘上方向(变成矢量)、取反、乘以系数
- 再次理解:红框内做向量点乘、求出一个数,然后再乘以单位方向变成矢量
- 注意:摩擦力跟弹力是不同的,不需要考虑弹簧本身的长度,而考虑相对速度
- 需要添加摩擦力(damping),让弹簧能够停止
- 最后,把弹力和摩擦力都考虑,就得到基本单元(一节弹簧)的物理模型
组合模型(布的物理模型)
通过组合一节弹簧,就得到各种形状的物理模型
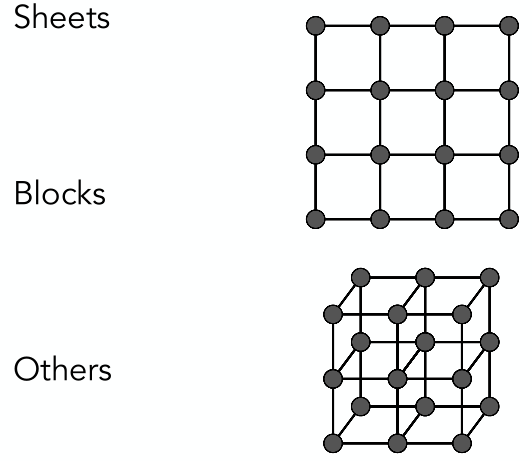
- 考虑组合成上图的上面的结构,来模拟布的物理模型
- 问题一:切变会受影响,如果拉着两个角,形状会被拉长,而真实的布会抵抗切变力、不会形变
- 改进:加入斜的对角线,如果沿着↙、↗拉动结构,↖、↘方向的弹簧会被压缩、产生对抗变化的力

- 此外,这个结构可以抵抗斜着的弯折,弹簧被折后会有复原的趋势
- 然而,这个结构不能抵抗竖直、水平的弯折
- 问题二:现实的布也会有对抗 out-of-plane bending 的性质,也就是不能像纸一样被轻松折,在这个结构中也无法体现
- 改进:任一个点跟隔一个点连接一条弹簧,这样不管怎样弯折都会引起弹簧的形变了

- 此外,红线的连接弱一些(对应现实中的布也会被弯折),只起辅助作用,而主要还是蓝线的连接。因此也不能只采用红线而不使用蓝线
- 问题一:切变会受影响,如果拉着两个角,形状会被拉长,而真实的布会抵抗切变力、不会形变
- 这样就是描述布料的简单的物理模型了,可以模拟一些简单的效果
- 如果想要布料跟人体动作的配合,还需要有摩擦力等其他模型
- 在前面讲过,真实的布料是纤维缠绕形成股、股缠绕形成线、线经过不同编织方法得来的,物理模拟通常是对真实世界的简化的表示方法
除了质点弹簧系统,也有其他的系统用来建立物理模型
- FEM(Finite Element Method)有限元方法,被广泛应用于汽车碰撞
- 接触墙的地方受力,但力会传导到整个车子,就像热的传导一样
- 这种力和热的传导被称为 Diffusion 扩散,适合用有限元方法来做
Particle Systems 粒子系统
粒子系统基本
- 粒子系统是什么
- 并不是所有的东西都适合用质点弹簧系统来建模。对于一堆很小的东西,通常使用粒子系统来建模
- 把每一个粒子都建模出来
- 定义每一个粒子收到的力,分为内部的力(粒子之间的碰撞、引力等)、外部的力(重力、风力等)
- 进行模拟
- 并不是所有的东西都适合用质点弹簧系统来建模。对于一堆很小的东西,通常使用粒子系统来建模
- 粒子系统的应用
- 适合于营造魔法的效果,模拟雾、灰尘等运动,在游戏中得到广泛的应用
- 也可以做一些其他的效果,比如流体模拟可以把水看作一个整体,也可以考虑每个小水滴的运动情况
粒子系统的实现
- 粒子系统的挑战
- trade-off:粒子越多越精细,但计算也越慢
- 实现不容易。或许需要用到加速结构,比如计算粒子之间的引力时,需要查找最近的 n 个粒子
- 粒子系统的实现方法(简单描述),对于动画的每一帧:
- (如果需要)创建新的粒子
- 计算每个粒子的受力(modeling,决定粒子性质的一步,到底模拟的是水滴还是雾)
- 更新每个粒子的位置、速度(如何解。是学术界更关注的部分)
- (如果需要)删除废弃粒子
- 渲染所有粒子
- 更多需要考虑的力
- 重力,电磁力,弹簧力,斥力,吸引力(如图),…
- 摩擦力,空气阻力,粘滞力,…
- 跟墙、容器的碰撞(防止穿模),跟其他粒子的碰撞

概念延申的粒子系统
- 粒子系统不一定只用来描述简单的点:在大规模的范围内,有很多小的重复的东西,这些东西就可以被理解为粒子
- 群体中的个体,如模拟鸟群。考虑鸟会接近鸟群,但避免跟其他鸟过于接近,并且倾向于朝向平均方向
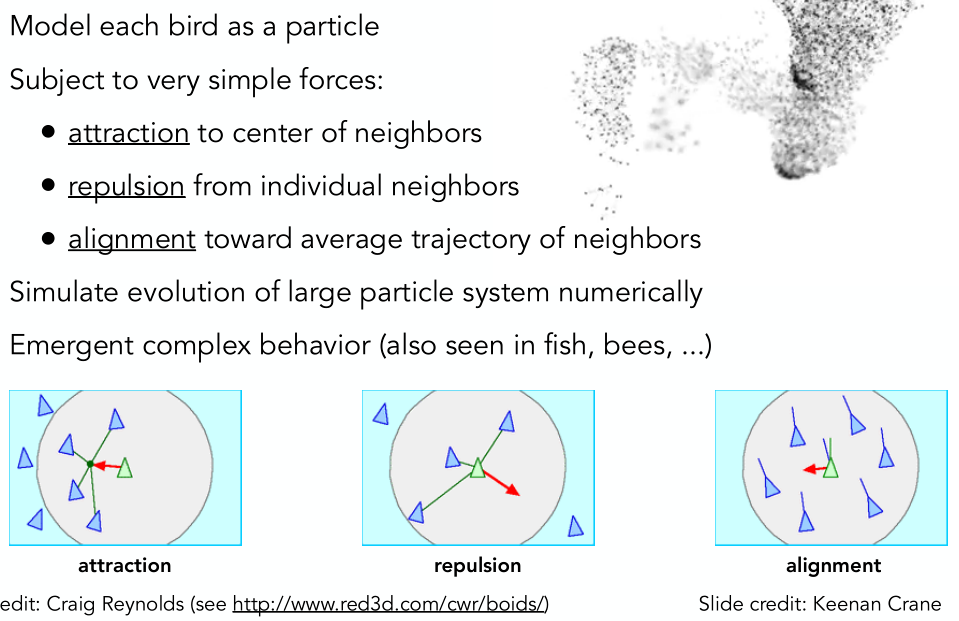
- 粒子系统本质上就是定义个体与群体的关系。也可以用来模拟鱼群、蜜蜂、分子运动等等,每个粒子的行为也可以复杂,比如用来模拟人群
4 - Kinematics 运动学
Forward Kinematics
骨骼系统
描述一个骨骼系统,表示跟人的骨骼连接类似的拓扑结构。通过定义、组合不同的简单关节,形成相连的复杂模型
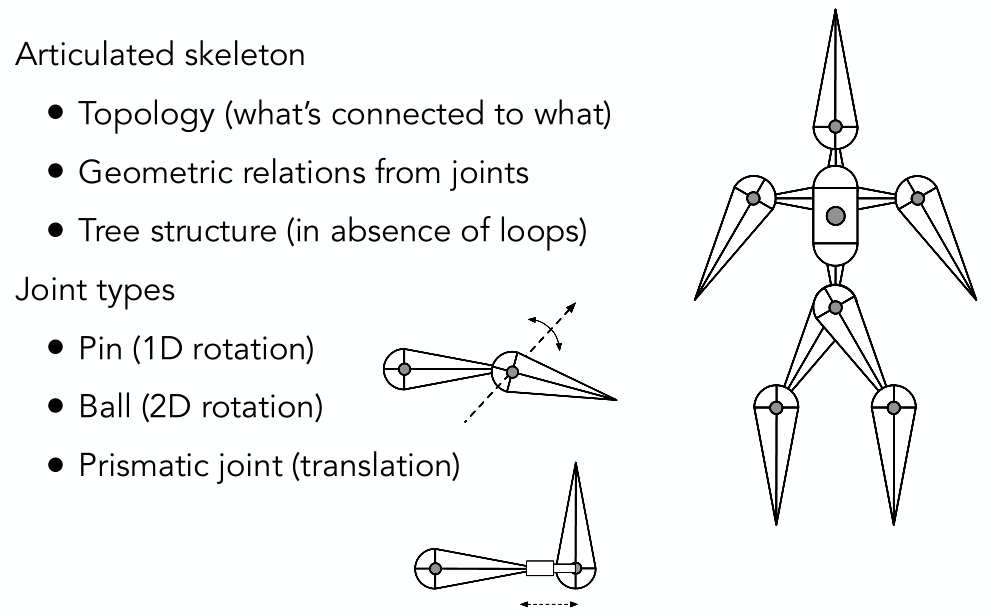
- Pin 钉子关节,在钉住的平面内旋转
- Ball 球关节,可以自由旋转
- Prismatic joint,可以移动、拉长
整个模型可以组织成一个树形结构
正向运动学:Animator 提供连接方式、旋转的角度等信息,需要计算各个点运动到什么位置
- 以图中的 Pin 关节为例,知道了两个关节的旋转情况和长度,计算机需要求出关节末端的坐标
- 优点:实现容易,计算方便
- 缺点:正向运动学的定义都非常物理,但艺术家们不喜欢这样创作,需要更加直观的动画创作方式
Inverse Kinematics
逆向运动学:直接调节尖端的位置,关节自动调整位置和角度
- 缺点:计算非常复杂,并且通常解不唯一,并且有时不存在解
- 正常情况下,采用一些优化方法,来找到关节对应的位置
- 定义优化问题:已有最后的结果坐标,如何找到几个角度和位置,满足整个结构的末端位于结果坐标
- 对于优化问题,通常用机器学习中的梯度下降法来解,或者用牛顿法等其他数值方法,而不是通过数学来求
5 - Rigging
控制点 Rigging
Rigging 指的是对于一个形状的控制,类似于“木偶”的操作,一定程度上是逆运动学的一种应用
- 对于一个角色,给它不同的控制点,通过拉拽这些点做出不同的运动。可以联想贝塞尔曲线的控制点
- 使用
- 在电影界,会应用 Rigging,给模型添加动作、做各种造型,包括面部表情、肢体动作等
- 在美术工作中,具体需要给物体定义控制点、加上骨骼,包括软选取、蒙皮等步骤
- Blend Shape:可以把两个形状混合到一起,但实际上不是在混合 shape,而是在混合控制点和周围能影响到的区域,具体的 blend 过程需要各种曲线的定义
Motion Capture
- 可以给模型加上不同的控制点、做 Rigging 来生成动画,也可以给真人加上控制点,让控制点的位置直接反应到虚拟造型上去
- 优点:可以直接把人的动作转移到动画中去,迅速、真实,不需要美术去调,可以方便地生成大量数据
- 缺点:设备复杂,有时捕捉不到好的数据
- 除了直接通过白点,经过视觉的方法识别,也可以有电磁或机械的多种方法,完成人和模型的控制点之间的映射。其中应用最广泛的是光学的方法,贴一些 Markers、用很多复杂的摄像机,准确地捕捉动作
Misc.
其他一些问题
感知上的问题:Uncanny valley(恐怖谷效应)
技术上的问题:面部的动作捕捉,更加细微
动画生产的Pipeline
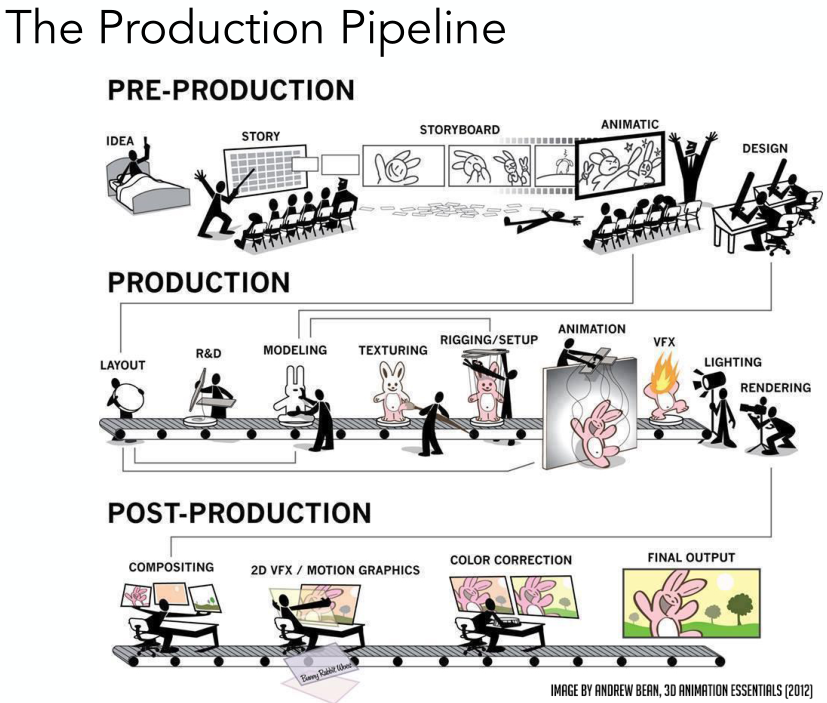
- 第一行:设计阶段。对整体有基本把握,包括各个场景的样子、故事、模型的运动
- 第二行:进入产品线,进行实际操作。如布置场景、主人公建模、制作材质、使用 Rigging 制作造型、形成动画、Lighting、VFX(visual effects)、Rendering 等,把主人公和场景结合到一起
- 第三行:后处理。组合、2D 的滤镜效果、调色等
Lecture 22 - Animation Cont.
- Single particle simulation
- Explicit Euler method
- Instability and improvements
- Rigid body simulation
- Fluid simulation
1 - Single Particle Simulation
单个粒子模拟问题——求解常微分方程
规定了物体任何一个时刻的速度,知道物体开始出现的位置,求解:在某个时间之后物体出现在哪里
首先,考虑一个单个粒子的运动情况
- 定义一个理想的情况:物体在速度场中。可以得到粒子在任一位置、任意时刻的速度 $v(x,t)$
- Ordinary Differential Equation (ODE) 常微分方程
- $\frac{dx}{dt}=\dot x=v(x,t)$
- 常微分方程:知道一个量的微分是多少,希望求出这个量是多少。常微分方程只有单个变量
- 在此处,知道速度、想求得位置。具体来说,给定起始位置 $x_0$,知道任意时间速度 $v(x,t)$,想要求得在任何时间 $t$ 的位置 $x$
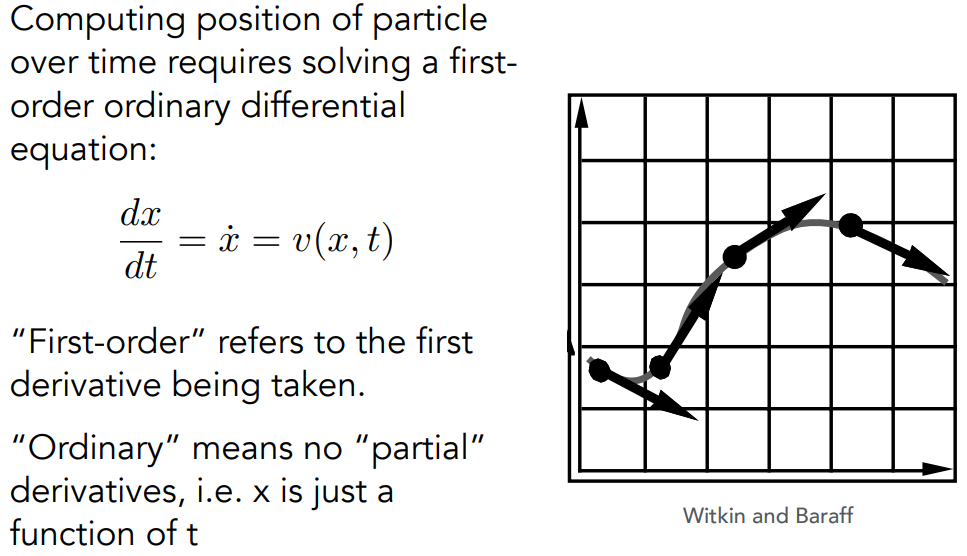
Explicit Euler method
Euler’s Method(Forward 前向欧拉 / Explicit 显式欧拉)
- $x^{t+\Delta t} = x^t + \Delta t \dot x^t$,$\dot x^{t+\Delta t} = \dot x^t + \Delta t \ddot x^t$
- 把时间分成很多小块(离散化),每一步不断加上步长的时间,用上一个时刻的量估计这一时刻的量
- 问题:
- 不准,有误差。通过缩小 $\Delta t$,可以减小误差
- 稳定性不好,越模拟离现实情况越远。如下图上方,不管取什么样的步长,最后都会离开螺旋型的速度场;下方,随着模拟,不会走向水平,而变化会越来越大
- 不准,有误差。通过缩小 $\Delta t$,可以减小误差
- 对于使用数值方法求解微分方程,都会面临两个问题
- Errors 误差:每一步计算都有误差,累积起来也会有误差。如果用较小的步长,就会降低误差。此外,图形学关注视觉效果,而不是物理上的正确,一定范围内的误差可以被接受
- Instability 不稳定:“diverge”,有任何一个模拟方法,但模拟得到的结果都跟正确结果差得越来越远
Instability and improvements
由于欧拉方法的不稳定性质,有一些其他的求解微分方程的方法,可以在一定程度上解决不稳定性
方法一 Midpoint Method
中点法
- 第一,从起点应用欧拉方法,得到点 a;第二,取起点跟 a 点的中点,记录中点处的速度;第三,回到起点,使用中点的速度,应用欧拉方法
- 把式子展开后会发现,中点法比欧拉法多了二次项。中点法(或叫做 Modified Euler 改进欧拉法)不再是线性的估计模型,而是局部的二次模型,更加准确
方法二 Adaptive Step Size
- 把欧拉方法和中点法结合起来:第一,在 $\Delta t$ 应用欧拉方法,得到一个点;第二,把 $\Delta t$ 分成两半,在两个 $\Delta t/2$ 依次应用欧拉方法,得到第二个点;第三,如果这两个结果差不多,就不再继续进行,如果差得远,就把 $\Delta t/2$ 继续往下分
- 借用了中点的思想。不是应用中点的速度、从起点出发,而是在中点再进行一次欧拉方法
- 最终,在不同的地方会选择不同的 $\Delta t$ 的大小,是一种 Adaptive 自适应的方法
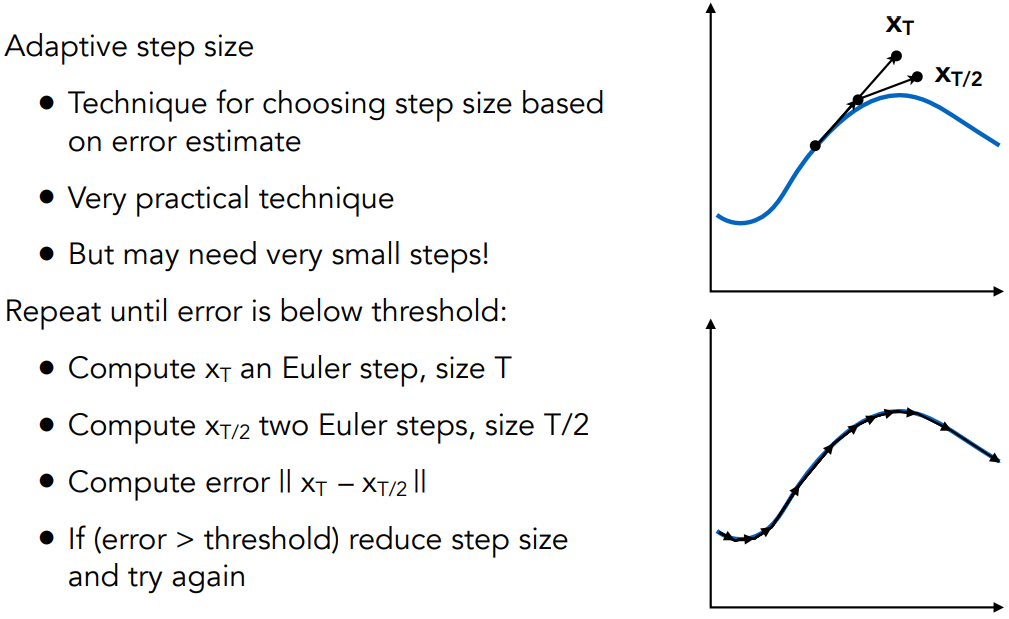
方法三 Implicit Euler Method
隐式(Backward 后向)欧拉方法,使用下一个时刻的信息更新这个时刻的信息
- 显式:$x^{t+\Delta t} = x^t + \Delta t \dot x^t$,$\dot x^{t+\Delta t} = \dot x^t + \Delta t \ddot x^t$
- 隐式:$x^{t+\Delta t} = x^t + \Delta t \dot x^{t+\Delta t}$,$\dot x^{t+\Delta t} = \dot x^t + \Delta t \ddot x^{t+\Delta t}$
- 不易求解,通常用优化方法(牛顿法,求根公式等)
如何定义、度量稳定性?
- 每一步度量 local 误差,累计成 total 误差,用这两个量衡量稳定性
- 研究这两个数是没有意义的,应该研究它们的阶,也就是它们跟取的 $\Delta t$ 的关系
- 误差会随着取更小的 $\Delta t$ 而减小。具体是如何减小的?它们之间是什么样的关系?这是要研究的问题
- 结论:Implicit Euler Method 是一阶的
- Local truncation error: $O(h^2)$
- Global truncation error: $O(h)$
- $h$ 是步长,在这里就是 $\Delta t$
- 理解 $O(h)$ :
- 如果把 减小一半,那么最后的误差也会减小一半
- 阶数越高越好($\Delta t$ 减小一些,误差减小得更多)。用阶数来衡量一个数值方法的稳定性
方法四 Runge-Kutta Families
龙格库塔方法,是一类方法,非常适合于解常微分方程,特别是对于非线性的情况
- 对于场扭曲得厉害的情况,中点法比前向欧拉法好(中点法是平方模型、前向欧拉是线性模型),而龙格库塔更加好
- 四阶的龙格库塔方法是最广泛使用的方法,aka RK4
- 可以看到,更新方法是在两个点之间取了几个中间点,进行平均

方法五 Position-Based / Verlet Integration
不是基于物理的方法,只是一些计算
- 通过一些非物理的方式,直接改变位置。原理简单、实现快,但不满足一些性质(如能量守恒)
- 在之后的流体中,介绍一个具体例子,调整不同粒子的位置
- 这个方法不基于物理,但在某些模拟中好用。在 HW8 里实现
2 - Rigid Body Simulation
Rigidbody 是刚体的概念。刚体不会发生形变,它内部所有的点都按照同一种方式进行运动。整个刚体可以看作一个粒子运动。
在刚体模拟中,会更多考虑其他物理量
- 在原本的位置基础上,又会考虑它的速度、角速度等物理量。因为刚体很大,需要一些物理量计算它每一个点的运动方式
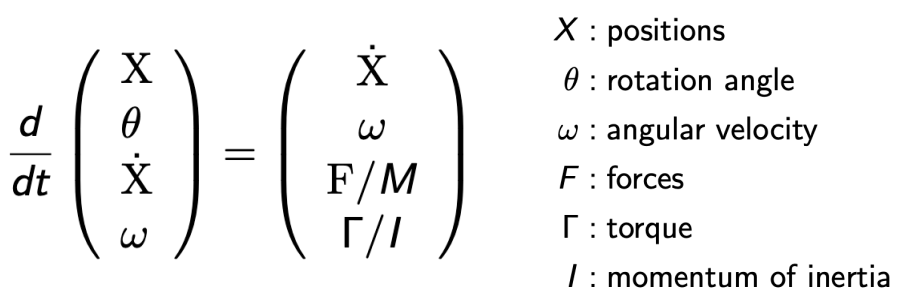
- 位置求导是速度,角度求导是角速度,速度求导是加速度,角速度求导是角加速度
- 可以看作是对粒子进行一些扩充,在这之后,就利用之前的各种数值方法,求解任何时间 $t$ ,刚体对应的位置和旋转方式
3 - Fluid Simulation
流体模拟有不基于物理的方法,也有基于物理的方法
A Simple Position-Based Method
Key idea
整个水体是由很多不可压缩的刚体小球组成的。计算出每个小球的位置,然后进行渲染即可
基本假设:水在任何一个地方都是不可压缩的,const density
给定任一时刻,对于如果有一个地方,水的密度发生改变(跟平静时的密度不一样),那么就需要把密度“修正”过来
- 通过移动小球的位置,使得任意一个密度不正确的地方被修正
- 为了做修正,需要知道任何一个点的密度对所有小球位置的梯度是多少。比如,考虑一个点的密度跟它周围小球的位置的导数,如果小球的位置改变了,这个点的密度也会发生改变
具体的修正过程中,对于任何一个位置,想要让不正确的密度回到正确的密度,并且知道如何调整各个小球的位置、使得密度向想要的方向变化,这就是机器学习中 gradient descent 的过程(想要目标跟某个结果相似,就让当前状态往目标状态变化)

这不是基于物理的模拟,不需要用到欧拉法等方法,而是在任何一个时间,都知道任何一个小球应该如何进行位置变化
因此,也会无止境地修正、运动下去。可以再添加一些能量衰减的系统,使得水最后回归到静止状态
Eulerian vs. Lagrangian
在物理模拟中,模拟大规模物质用到的两个基本思路
- Lagrangian Approach 拉格朗日方法 / 质点法:
- 考虑每个个体的运动情况
- 盯着物体看
- Eulerian Approach 欧拉方法 / 网格法:
- 看待一系列大规模物体,把整个空间分成网格,不考虑网格中个体的进出,而考虑网格随着时间如何变化
- 盯着某个固定空间看:对于中间的网格,t 时刻是黑色的鸟,t-1是橙色的鸟要飞走,t+1是蓝色的鸟飞过来(鸟向右飞)

也有工作将两种方法结合
- 首先,认为不同粒子都具有某些材质属性;然后,融化的过程在格子里做、考虑不同的格子,将信息记录在格子上;最后,把格子记录的信息写回到每个粒子个体中

4 - 展望
Rasterization
- 图形API
- 实时渲染:《Real-time Rendering》 + OpenGL
- Real-time Ray Tracing,DXR,跨平台的 Vulkan 等
- 各种不同的着色器,顶点和片段
Geometry
- 数学基础,微分几何、离散微分几何,拓扑,流形
Light Transport
Animation / Simulation
- GAMES 201
Real-Time High Quality Rendering(GAMES 202)
- Soft Shadows and Environment Lighting
- Precomputed Radiance Transfer
- Image-Based Rendering
- Non-Photorealistic Rendering
- Interactive Global Illumination
- Real-time Ray Tracing & DLSS, etc.
Advanced Image Synthesis
- Part 1: Advanced Light Transport
- Part 2: Advanced Appearance Modeling
- Part 3: Emerging Technology for Rendering
- Foundations for rendering research! 开启 rendering 的科研之路
最终目标:做到真正的“以假乱真”:
实时渲染,离线渲染:解决已知的问题,比如全局光照怎么做
外观建模:解决未知的问题,比如不知道动物的毛发应该如何渲染,就进行一些建模
成像:未来设备,不同成像方式
新的技术